6. Дифференциальные уравнения равновесия (уравнения Эйлера)

Из лекции Исаковой:

Дифференциальные уравнения равновесия флюида в поле силы тяжести (уравнения Эйлера)

Точка M – центр тяжести элементарного объёма dV

Для 0Y:

F_y-F_y+dy+F_my=0

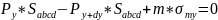
S_abcd=dxdz

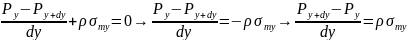
Система уравнений Эйлера определяет закон распределения давления вдоль соответствующей оси координат. То есть смысл этих уравнений – соотношение между силами действующими на жидкость, которая находится в состоянии покоя, определяющее условия равновесия жидкости

7. Уравнение поверхностей уровня (изобарических поверхностей) и их свойства.

В поле сил тяжести: (изобарные поверхности)

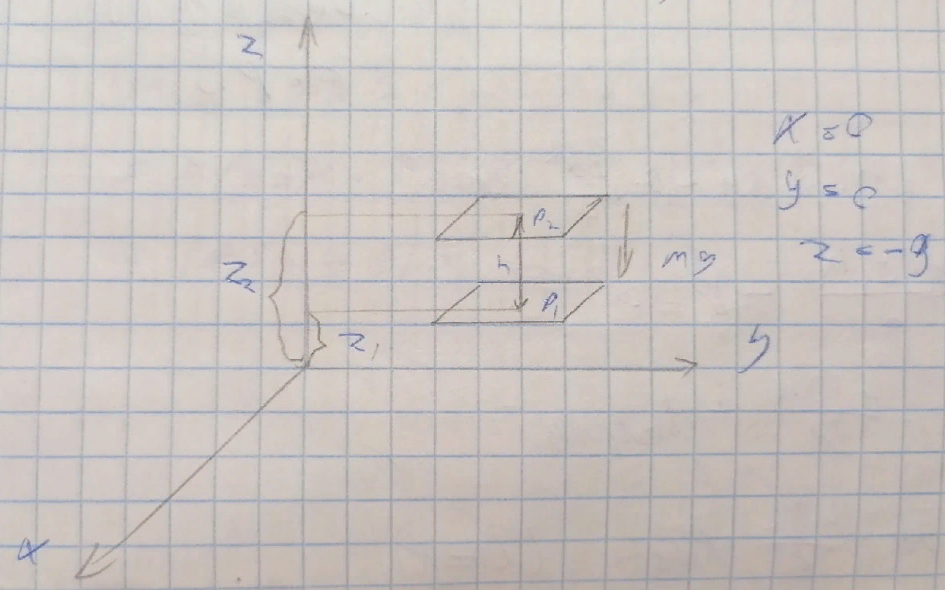
В поле сил тяжести:

Поэтому:

Свойства:

1. Изобарические поверхности не пересекаются друг с другом

2. Через каждую точку флюида можно провести одну и только одну изобарическую поверхность

3. Вектор массовой силы перпендикулярен изобарной поверхности.

8. Основное уравнение гидростатики несжимаемой жидкости.

Выписать из 7 вывод dP с рисунком; про 3 вида давлений при этом писать необязательно.

В случае несжимаемой жидкости её плотность не зависит от давления, а если принять температуру постоянной, то можно записать: ρ=const

Для высот в несколько метров ускорение силы тяжести можно считать неизменным. Таким образом, можно подсчитать разность давления между точками М₁ и М₂. Проинтегрировав выражение dp= -ρgdz, можно получить разность давлений между двумя точками:

Выводы:

1. В покоящейся жидкости давление увеличивается с увеличением глубины.

2. В покоящейся жидкости любая горизонтальная плоскость представляет собой поверхность, на которой в любой точке давление будет неизменным. Такая поверхность называется поверхностью равного давления.

Всего существует 3 формы записи этого уравнени:

1. Было получено выше – в форме давлений, так как каждый член уравнения представляет собой давление:

p₁ и p₂ – статическое давление в точках 1 и 2

ρgz₁ и ρgz₂ – давление, создаваемое силой тяжести.

2. Если разделить основное уравнение в форме давлений на ρg, то получим основное уравнение в форме напоров

Рисунок 1 Геометрический и пьезометрический напоры

3. Если разделить основное уравнение в форме давлений на ρ, то получим основное уравнение в форме удельной энергии

9. Сила давления жидкости на плоские твердые поверхности. Точка приложения равнодействующей силы.

L – расстояние от dS до п.п.

L_T – расстояние от центра тяжести стенки до п.п.

L_D – расстояние от центра давления стенки до п.п.

h – вертикальное расстояние от элементарной площадки dS до п.п.

h_T – вертикальное расстояние от центра тяжести плоской стенки до п.п.

Центр давления и центр тяжести совпадают только для газа

P=dF/dS → dF = PdS → dF= (ρgh+Pат)dS

h=l*sinα

F=P_атS+ ρgh_TS = S*( P_ат+ ρgh_T)

Для заделанной стенки (ведро на полу):

F=(Pат+Pт)*S, где Pат+Pт=Pабс

Для незаделанной стенки:

F= ρgh_TS= Pт*S

Центр давления:

Где l_T и l_D – расстояния от пьезометрической поверхности, отсчитываемые вдоль продольной оси симметрии смоченной части твердой плоскости до её центра тяжести и центра давления соответственно. Второе слагаемое в правой части уравнения есть смещение «а» центра давления относительно центра тяжести. Y – момент инерции, w – площадь поверхности.