35. Основные понятия и определения подземной гидромеханики.
Подземной гидромеханикой называется наука, которая изучает законы равновесия и движения воды, нефти, и/или газа, и/или газожидкостных смесей (флюидов) в пористых и трещиноватых средах – подземных пластах, которые являются коллекторами флюидов – УВ сырья и/или воды. Движение флюидов в пористой среде называется фильтрацией.
M=Vп/V – пористость. Под ней понимают отношение объёма пустот представительного физически малого объёма к его объёму
S(n)=Sп/S – просветность пористой среды (поверхностная пористость). Под ней понимают отношение площади просветов в сечении образца среды к площади всего сечения
n – вектор нормали к плоскости сечения.
Проницаемость
Фильтрация
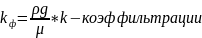
Скорость фильтрации
(1.8)
– скорость перемещения флюида в пористой
среде
36. Опыт и закон Дарси.
Опыт Дарси
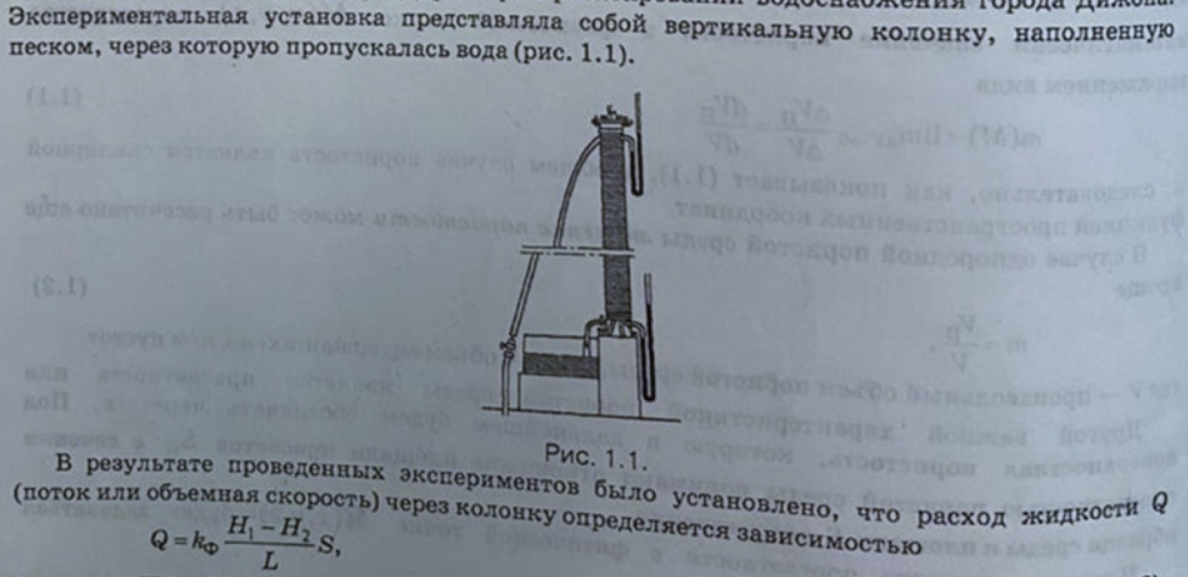
Закон дарси
Экспериментальное соотношение (1.8), полученное для установившейся прямолинейно-параллельной фильтрации в однородной изотропной недеформируемой пористой среде, задает линейную зависимость между модулем вектора скорости фильтрации ω и отношением Δp*/L. Если умножить равенство (1.8) на орт n, задающий направление вектора скорости фильтрации, получим:
Осуществляя в (1.10) обычный предельный переход, получаем обобщение экспериментального результата в виде дифференциальной формы записи закона Дарси для изотропной среды
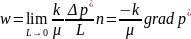
Знак минус в правой части равенства указывает на то, что скорость фильтрации направлена в сторону уменьшения давления, в то время как градиент направлен в сторону его роста
37. Границы применимости закона Дарси.
Закон Дарси имеет силу, если соблюдаются следующие условия:
1) мелкозернистая пористая среда или достаточно узкие поровые каналы;
2) малая скорость фильтрации при небольшом градиенте давления;
3) незначительные изменения скорости фильтрации или градиента давления.
Закон Дарси справедлив для медленных фильтрационных движений, для которых силы инерции несущественны. Поэтому для таких движений несущественна плотность жидкости, определяющая свойство ее инерции.
При малых скоростях течения природа нелинейности закона фильтрации иная, чем в области больших скоростей фильтрации (больших значений числа Рейнольдса). Она связана с проявлением неньютоновских свойств фильтрующихся флюидов, а также других физико-химических эффектов и больших поверхностных сил (сил взаимодействия между флюидом и твердым скелетом).
Верхняя граница определяется группой причин, связанных с проявлением инерционных сил при высоких скоростях фильтрации. Верхнюю границу применимости закона Дарси связывают обычно с некоторым критическим (предельным) значением Reкр числа Рейнольдса.
Формулы для вычисления Re и их критические значения были предложены несколькими учеными:
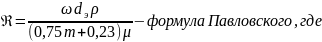
w – скорость фильтрации
dэ
– эквивалентный диаметр
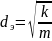
m – пористость, ρ – плотность, μ – динамическая вязкость;
7,5 ≤ Reкр ≤ 9
Где k – коэффициент проницаемости;
0,22 ≤ Reкр ≤ 0,29
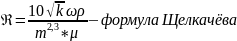
1 ≤ Reкр ≤ 12
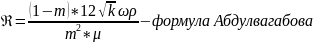
0,019 ≤ Reкр ≤ 8,1
Если Re < Reкр, то закон Дарси выполнен