Министерство цифрового развития, связи и массовых коммуникаций

Российской Федерации

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ

(МТУСИ)

Факультет "Радио и телевидение"

Кафедра "Техническая электродинамика и антенны"

УДК 621.3

Курсовая работа

По дисциплине "Устройства СВЧ и антенны":

"Разработка двухзеркальной антенны Кассегрена для искусственного спутника Земли"

Вариант 4(7)

Выполнил:

Студент группы

Проверил:

Вариант № 4

Техническое задание

Спроектировать двухзеркальную антенну Кассегрена. Антенна устанавливается на борту искусственного спутника Земли (ИСЗ) и осуществляет передачу на Землю линейно-поляризованных сигналов на частоте. ИСЗ находится на стационарной орбите и предназначен для ретрансляции телевизионных сигналов на радиолинии Земля-ИСЗ-Земля.

В таблице указаны технические параметры для аппаратуры:

– мощность бортового передатчика ;

– мощность на входе наземного приемника и коэффициент усиления приемной антенны на Земле ;

– потери в фидерных трактах радиопередающей и приемной антенн дБ;

– потери в атмосфере Земли в расчетах не учитывать. Протяженность радиолинии ИСЗ-Земля составляет км.

Исходные данные:

Двухзеркальная антенна

(краткая теория)

Двухзеркальная антенна обладает рядом достоинств по сравнению с однозеркальной, основными из которых являются:

– повышение коэффициента использования поверхности раскрыва (КИП) за счет наличия второго зеркала, облегчающего оптимизацию выравнивания распределения амплитуд в раскрыве основного зеркала;

– уменьшение длины тракта питания между приемо-передающей аппаратурой и облучателем и конструктивные удобства, связанные с размещением аппаратуры за основным зеркалом вблизи его вершины.

Принцип действия таких антенн заключается в том, что по методу геометрической оптики сферическая волна, излучаемая источником с фазовым центром, совпадающим с одним из фокусов гиперболоида, в результате переотражения от него преобразуется снова в сферическую волну, но с фазовым центром, совпадающим с другим фокусом. Действие параболического зеркала заключается в том, что при совпадении его фокуса с фокусом гиперболоида сферическая волна после отражения преобразуется в плоскую. Плоский волновой фронт перпендикулярен фокальной линии параболоида, и, следовательно, его раскрыв возбужден синфазно.

Двухзеркальная антенна может быть сведена к эквивалентной ей по закону распределения поля в раскрыве однозеркальной антенне того же диаметра, но с измененным фокусным расстоянием и углом раскрыва. Увеличение фокусного расстояния способствует получению более высокого апертурного КИП и сопровождается менее жестким требованием к точности установки облучателя в фокусе.

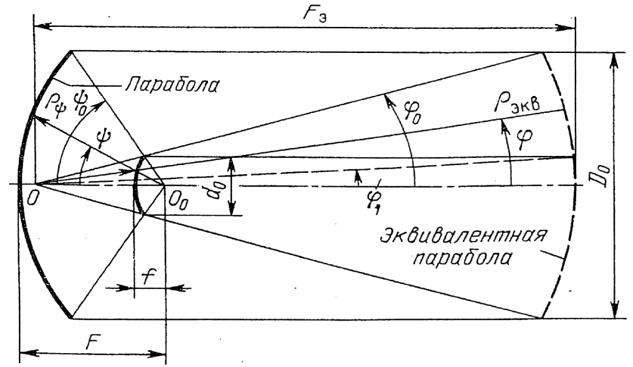
Рисунок 1 – двухзеркальная антенна и эквивалентная однозеркальная

В соответствии с рисунком 1 уравнение параболы: (1)

а уравнение эквивалентной параболы: , (2)

где ; e – эксцентриситет гиперболы.

Фокусные расстояния большого зеркала и эквивалентного параболоида связаны соотношением:

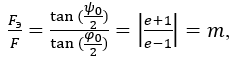(3)

где m – коэффициент увеличения;

– половина угла раскрыва основного зеркала;

– половина угла раскрыва эквивалентного параболоида.

, (4)

где – диаметр эквивалентного параболоида.

Амплитудное распределение на раскрыве эквивалентного параболоида определяется диаграммой направленности облучателя и отношением ( – радиус раскрыва эквивалентной параболы и основного зеркала); оно не отличается от амплитудного распределения основного зеркала.

Двухзеркальная антенна эквивалентна однозеркальной с измененным фокусным расстоянием и при определенном угле обеспечивает максимальный коэффициент направленного действия (КНД).

Оптимальное значение угла зависит от диаграммы направленности облучателя. Для большинства используемых на практике облучателей, например рупорных, фазовые искажения в раскрыве которых не превышают допустимых ( в плоскости Е, – в плоскости H), этот угол соответствует ширине ДН облучателя на уровне – 10 дБ (0,1 – по мощности; 0,316 – по полю).

В последнее время в антеннах для космической связи широкое распространение получили рупорные облучатели с ДН, близкой к столообразной форме (рисунок 2).

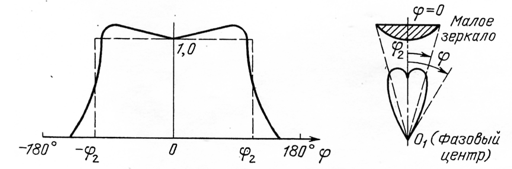
Рисунок 2 – диаграмма направленности

Такая ДН облучателя дает близкое к равномерному распределение поля в раскрыве зеркала, а быстрый спад распределения у краев обеспечивает минимальную утечку энергии облучателя и соответственно малый уровень излучения в задних квадрантах. Оптимальное облучение зеркала в этом случае может иметь место и при другом уровне освещения края антенны.

На практике наибольшее распространение находят антенны, построенные по схеме Кассегрена, из-за меньших осевых размеров и благодаря возможности реализации короткофокусных антенн ( , рисунок 1) с малым паразитным излучением в направлении за антенну.

Основные формулы, характеризующие геометрию антенн Кассегрена, имеют следующий вид:

Здесь в качестве независимых переменных взяты:

– диаметры большого и малого зеркал;

– половина угла раскрыва большого зеркала;

– угол облучения источником краев малого зеркала.

Для двухзеркальной антенны КНД равен: ,

где S = – площадь раскрыва;

– коэффициент использования поверхности раскрыва антенны.

двухзеркальных антенн можно представить в виде произведения:

где – апертурный КИП;

– коэффициент перехвата энергии облучателя малым зеркалом;

– коэффициент, учитывающий эффект затенения поверхности раскрыва малым зеркалом;

– коэффициент, учитывающий неточность выполнения поверхности параболического зеркала;

– коэффициент, учитывающий рассеяние мощности облучателя на кромках большого и малого зеркал и на элементах их крепления, переход части излученной мощности в кросс-поляризационную составляющую поля и т.д.

Для расчета ДН антенны следует исходную двухзеркальную антенну заменить эквивалентной однозеркальной антенной, а затем определить распределение амплитуд поля по раскрыву этого эквивалентного зеркала. Распределение амплитуды поля по раскрыву эквивалентного зеркала определяется графическим способом с использованием ДН облучателя. Аппроксимацию построенного распределения следует производить аналитической функцией: .

Откуда: 1 + a₂ + a₄ = ∆₁,

1 + a₂(0,5)² + a₄(0,5)⁴ = ∆₂.

После определения коэффициента и ДН антенны определяется из соотношения:

где – лямбда-функция n–го порядка;

;

– угол, отсчитываемый от нормали к поверхности зеркала.

Для вычисления надо использовать соотношение:

,

где – функция Бесселя n–го порядка, .

Расчетная часть