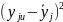1.5 Проверка гипотезы нормального распределения для данных опытов, с использованием многостороннего критерия
Проверим гипотезу нормального распределения, используя критерий Шапиро-Уилка, поскольку он применим для выборок объёмом 8 ≤ n ≤ 50. Критерий определяется по формуле (1.5).
, (1.5)
где
,
n – объём выборки,
m2(j) – выборочный центральный момент второго порядка.
Промежуточная сумма Q вычисляется по формуле (1.6).
, (1.6)
где k – индекс, имеющий значения от 1 до n/2 или от 1 до (n-1)/2 при четном и нечетном n соответственно,
ak – коэффициент критерия Шапиро-Уилка.
Последующие расчёты выполняются по аналогии, что видно из таблицы 1.7.
Далее нужно составить ранжированный ряд каждой строки, найти разность максимальных и минимальных значений по формулам в таблице 1.8, используя табличное значение коэффициента ak, найти промежуточную сумму Q и критерий W, что видно из таблицы 1.9.
Таблица 1.7 – Вычисление оценки дисперсии nm2(j)
№ |
|
nm2(j) |
|||||||||||||
1 |
0,061 |
4,218 |
3,818 |
2,710 |
6,483 |
18,030 |
4,218 |
1,094 |
0,199 |
0,021 |
1,572 |
3,788 |
24,541 |
70,752 |
|
2 |
1,710 |
8,455 |
31,274 |
7,332 |
6,720 |
6,212 |
1,982 |
0,258 |
3,639 |
1,982 |
10,941 |
13,633 |
1,193 |
95,329 |
|
3 |
32,315 |
1,477 |
17,511 |
30,419 |
1,477 |
1,176 |
1,730 |
2,204 |
5,361 |
6,840 |
2,609 |
0,969 |
5,686 |
109,777 |
|
4 |
2,414 |
6,021 |
7,584 |
9,898 |
7,002 |
3,076 |
3,408 |
0,557 |
18,889 |
8,725 |
0,910 |
8,101 |
9,947 |
86,532 |
|
5 |
0,866 |
5,432 |
7,125 |
38,059 |
12,036 |
8,589 |
2,159 |
0,690 |
0,072 |
10,438 |
1,143 |
3,352 |
9,186 |
99,148 |
|
6 |
14,323 |
2,511 |
2,609 |
1,650 |
37,398 |
23,859 |
15,330 |
8,908 |
0,081 |
12,143 |
8,499 |
0,046 |
12,358 |
139,717 |
|
7 |
12,521 |
19,905 |
21,730 |
0,545 |
4,250 |
6,561 |
38,918 |
0,001 |
25,386 |
8,188 |
6,961 |
1,349 |
0,213 |
146,531 |
|
8 |
1,160 |
0,006 |
1,496 |
1,385 |
0,077 |
10,093 |
11,043 |
3,523 |
6,881 |
0,179 |
7,166 |
1,261 |
2,634 |
46,903 |
|
9 |
0,616 |
15,090 |
4,908 |
13,804 |
8,321 |
16,684 |
0,379 |
11,456 |
45,096 |
8,499 |
0,469 |
3,552 |
2,003 |
130,877 |
|
10 |
0,024 |
1,572 |
8,680 |
45,614 |
0,120 |
3,818 |
3,408 |
2,414 |
7,584 |
11,248 |
60,003 |
11,876 |
2,091 |
158,452 |
|
11 |
6,212 |
0,258 |
0,037 |
3,639 |
0,796 |
5,797 |
0,000 |
2,273 |
0,369 |
4,442 |
0,479 |
2,864 |
9,562 |
36,729 |
|
12 |
0,469 |
11,456 |
0,034 |
1,917 |
2,296 |
6,680 |
2,511 |
2,296 |
1,730 |
11,665 |
0,469 |
5,361 |
0,173 |
47,057 |
|
13 |
0,242 |
2,585 |
5,325 |
0,037 |
4,874 |
23,935 |
0,985 |
0,369 |
6,720 |
10,191 |
10,941 |
2,585 |
0,501 |
69,289 |
|
14 |
3,581 |
43,662 |
41,059 |
1,227 |
38,345 |
0,369 |
0,501 |
16,747 |
10,191 |
14,382 |
15,270 |
0,0001 |
0,037 |
185,369 |
|
15 |
0,104 |
1,751 |
11,717 |
13,520 |
1,385 |
16,621 |
16,185 |
14,265 |
0,604 |
10,093 |
2,634 |
11,043 |
6,881 |
106,803 |
|
16 |
4,093 |
1,631 |
1,160 |
0,050 |
1,160 |
0,015 |
43,865 |
4,507 |
2,181 |
1,496 |
10,093 |
40,665 |
4,507 |
115,423 |
|
Таблица 1.8 – Вычисление разности максимальных и минимальных значений
k |
yk |
y(n+1-k) |
y(n+1-k)-yk |
ak |
ak·y(n+1-k)-yk |
1 |
1533,7 |
1542,9 |
9,2 |
0,5359 |
4,930 |
2 |
1536,6 |
1541,2 |
4,6 |
0,3325 |
1,530 |
3 |
1536,6 |
1540,6 |
4 |
0,2412 |
0,965 |
4 |
1536,7 |
1540,3 |
3,6 |
0,1707 |
0,615 |
5 |
1537,4 |
1539,7 |
2,3 |
0,1099 |
0,253 |
6 |
1538,8 |
1539,1 |
0,3 |
0,0539 |
0,016 |
Q1 = 4,93 + 1,53 + 0,965 + 0,615 + 0,253 + 0,016 = 8,308.
W1 = (8,308)2 / 70,752 = 0,976.
Последующие расчёты выполняются по аналогии с предыдущими.
Таблица 1.9 – Вычисление критерия Шапиро-Уилка
№ |
Q |
W |
№ |
Q |
W |
1 |
8,308 |
0,976 |
9 |
11,143 |
0,949 |
2 |
9,317 |
0,911 |
10 |
12,471 |
0,982 |
3 |
10,308 |
0,968 |
11 |
5,936 |
0,959 |
4 |
8,788 |
0,893 |
12 |
6,795 |
0,981 |
5 |
9,581 |
0,926 |
13 |
8,104 |
0,948 |
6 |
11,583 |
0,960 |
14 |
13,271 |
0,950 |
7 |
11,804 |
0,951 |
15 |
9,834 |
0,906 |
8 |
6,779 |
0,980 |
16 |
10,483 |
0,952 |
При уровне значимости α = 0,1, и числе наблюдений f = 13 табличное значение критерия Шапиро-Уилка составит W = 0,889. Поскольку табличное значение меньше всех вычисленных, нулевая гипотеза о нормальном распределении не отклоняется на уровне значимости α = 0,1.