1.8 Проверка воспроизводимости опытов
Чтобы провести проверку воспроизводимости используем критерий Кохрена, рассчитываемый по формуле (1.10).
, (1.10)
где
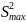– максимальное значение дисперсии,
– сумма
дисперсий.
= 15,447.
= 5,896 + 7,944 + 9,148 + 7,211 + 8,262 + 11,643 + 12,211 + + 3,909 + 10,906 + 13,204 + 3,061 + 3,921 + 5,774 + 15,447 + 8,9 + 9,619 = = 137,057.
=
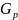15,447 / 137,057 = 0,1127.
Таблица 1.17 – Проверка воспроизводимости опытов
Результаты эксперимента (yju) |
|
||||||||||||
1538,9 |
1536,6 |
1537 |
1540 |
1541 |
1543 |
1537 |
1540 |
1539 |
1539 |
1537 |
1541 |
1534 |
5,896 |
1283,6 |
1285,2 |
1277 |
1285 |
1280 |
1280 |
1284 |
1283 |
1284 |
1284 |
1286 |
1279 |
1281 |
7,944 |
1599,4 |
1592,5 |
1598 |
1588 |
1593 |
1595 |
1592 |
1595 |
1591 |
1591 |
1592 |
1595 |
1596 |
9,148 |
1091,2 |
1090,3 |
1090 |
1096 |
1095 |
1091 |
1095 |
1094 |
1097 |
1090 |
1092 |
1096 |
1090 |
7,211 |
1035,3 |
1033,9 |
1039 |
1042 |
1040 |
1033 |
1038 |
1035 |
1037 |
1033 |
1037 |
1034 |
1033 |
8,262 |
1271,7 |
1273,9 |
1277 |
1274 |
1282 |
1271 |
1279 |
1273 |
1275 |
1272 |
1278 |
1276 |
1279 |
11,643 |
1058,9 |
1066,9 |
1067 |
1062 |
1065 |
1065 |
1056 |
1062 |
1057 |
1065 |
1060 |
1064 |
1063 |
12,211 |
796,9 |
795,9 |
795 |
797 |
796 |
799 |
793 |
798 |
793 |
795 |
799 |
795 |
794 |
3,909 |
1182,4 |
1185,5 |
1179 |
1178 |
1185 |
1186 |
1181 |
1185 |
1175 |
1179 |
1182 |
1184 |
1180 |
10,906 |
1287,4 |
1286,3 |
1291 |
1281 |
1288 |
1286 |
1289 |
1286 |
1285 |
1284 |
1295 |
1291 |
1289 |
13,204 |
1238,9 |
1235,9 |
1237 |
1235 |
1237 |
1234 |
1236 |
1235 |
1236 |
1234 |
1237 |
1238 |
1240 |
3,061 |
1099,6 |
1102,3 |
1099 |
1100 |
1097 |
1102 |
1101 |
1097 |
1098 |
1096 |
1100 |
1097 |
1099 |
3,921 |
1313,7 |
1315,8 |
1317 |
1314 |
1316 |
1309 |
1313 |
1315 |
1312 |
1311 |
1318 |
1316 |
1315 |
5,774 |
1190,6 |
1182,1 |
1182 |
1188 |
1195 |
1188 |
1188 |
1193 |
1192 |
1193 |
1185 |
1189 |
1189 |
15,447 |
1343 |
1344 |
1346 |
1339 |
1342 |
1339 |
1347 |
1339 |
1342 |
1340 |
1344 |
1346 |
1345 |
8,900 |
712,6 |
709,3 |
710 |
711 |
710 |
711 |
717 |
713 |
709 |
712 |
707 |
704 |
713 |
9,619 |
При a = 0,1, f1 = n-1 = 12, f2 = 16 табличное значение критерия равно Gкр = 0,1388. Расчётное значение оказалось меньше табличного, что говорит нам об однородности дисперсий, значит исследуемая величина подчиняется нормальному закону распределения.