Тема 9. Циклы и мосты, цикломатическое число. Фундаментальная система циклов графа.
1) Пути, цепи, циклы на графе
2) Отношение достижимости (связности), компоненты связности графа
Если 𝑘(𝐺) = 1, то граф называется связным. Иными словами, граф связный, если любая пара его вершин соединена путем.
3) Мосты графа, связь между мостами и циклами
4) Цикломатическое число графа
5) Линейное пространство циклов
6) Алгоритм построения фундаментальной системы циклов
Тема 10. Деревья.
1) Дерево, лес, их характеристические свойства
2) Остовы графа
3) Число остовов в графе с занумерованными вершинами
4) Алгоритм Краскала отыскания минимального остова
5) Кодирование деревьев
Выделим в дереве какую-нибудь одну вершину, которую назовем корнем. Полученное дерево с выделенной вершиной называется корневым. Для задания (с точностью до изоморфизма) корневых деревьев используют бинарный код (из 0 и 1), который мы определим индуктивно.
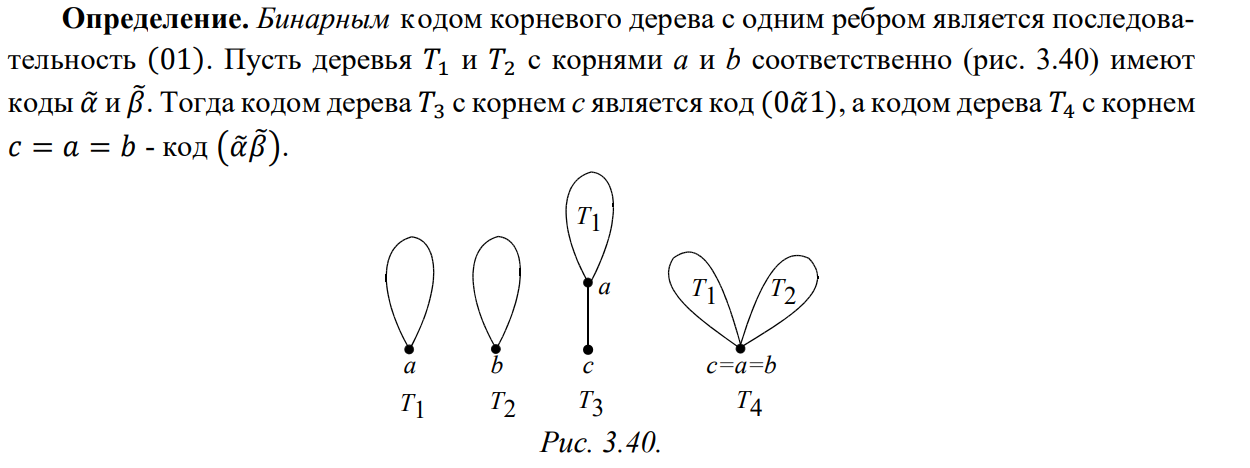
Справедливо следующее утверждение: для того чтобы последовательность нулей и единиц являлась кодом некоторого дерева, необходимо и достаточно, чтобы число нулей и единиц в последовательности было одинаковым, причем в любом начальном отрезке последовательности количество нулей было не меньше количества единиц.
Для задания деревьев c занумерованными вершинами используют код из натуральных чисел (код Прюфера). Код Прюфера для дерева с занумерованными вершинами строят следующим образом. Находят висячую вершину с наименьшим номером. Записывают номер смежной с ней вершины (это начало кода), после чего удаляют эту висячую вершину вместе с инцидентным ей ребром. Для полученного в результате данной операции дерева находят висячую вершину с наименьшим номером, записывают номер смежной с ней вершины (это продолжение кода), после чего удаляют эту висячую вершину вместе с инцидентным ей ребром. Так поступают до тех пор, пока не останется последнее ребро (его вершины в код не включают). Полученная в результате описанных действий последовательность и есть код Прюфера. Заметим, что длина этого кода на единицу меньше числа ребер и на две единицы меньше числа вершин дерева.
Тема 11. Планарность.
1) Укладка графов в трехмерном пространстве
Говорят, что граф обладает укладкой в пространстве, если в трехмерном евклидовом пространстве можно построить такую диаграмму графа, в которой ребра не имеют общих точек, отличных от концевых. Сама диаграмма, обладающая указанным свойством, называется при этом укладкой графа в пространстве.
2) Укладка графа на плоскости. Планарные графы
Говорят, что граф обладает укладкой на плоскости, если в двумерном евклидовом пространстве существует такая диаграмма графа, в которой ребра не имеют общих точек, отличных от концевых.
Граф, обладающий укладкой на плоскости, называют планарным. Любую укладку планарного графа на плоскости называют плоским графом.
3) Связь между числом вершин, ребер и граней плоского графа
4) Критерии планарности. Алгоритм укладки графа на плоскости
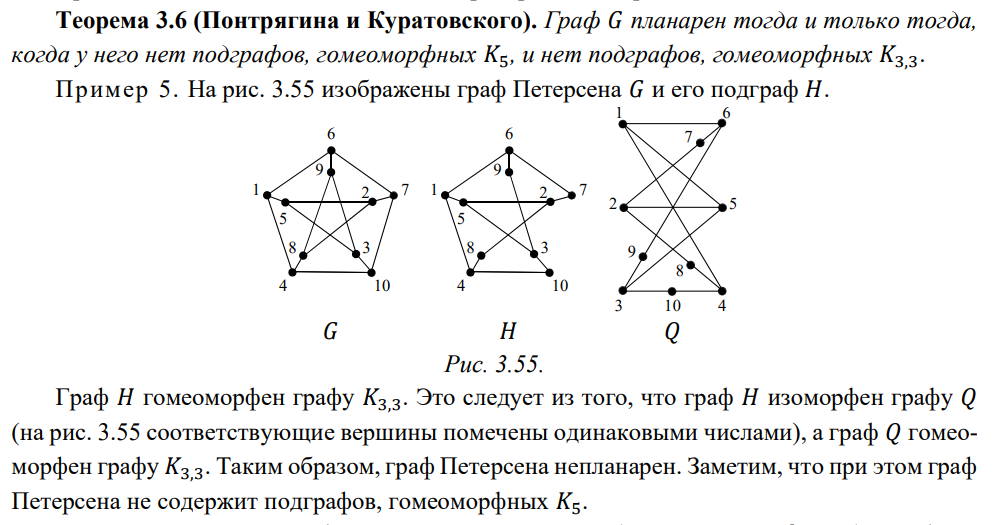
Почитать Алгоритм укладки графа на плоскости.