Тема 3. Булевы функции и способы их задания
1) Булев вектор - упорядоченный набор (𝛼1, 𝛼2, . . . , 𝛼i), где 𝛼i принимают значения 0 или 1. Числа 𝛼i называют координатами вектора, число 𝑛 - его длиной.
2) Функции алгебры логики (булевы функции) - функция, определенная на 𝐵^n и принимающая значение 0 или 1, называется булевой функцией от 𝑛 переменных.
3) Задание булевых функций таблицей истинности и вектором значений
4) Элементарные булевы функции одной и двух переменных
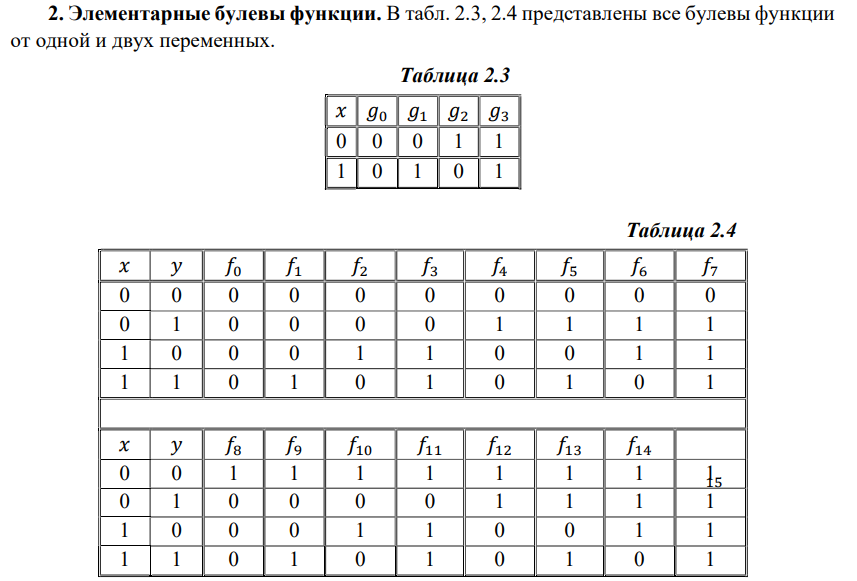
5) Формулы над множеством функций, задание функций формулами, равносильные формулы. Доказательство равносильности формул с использованием таблиц истинности
6) Основные равносильности над множеством {∨,∧, ¬,0,1}
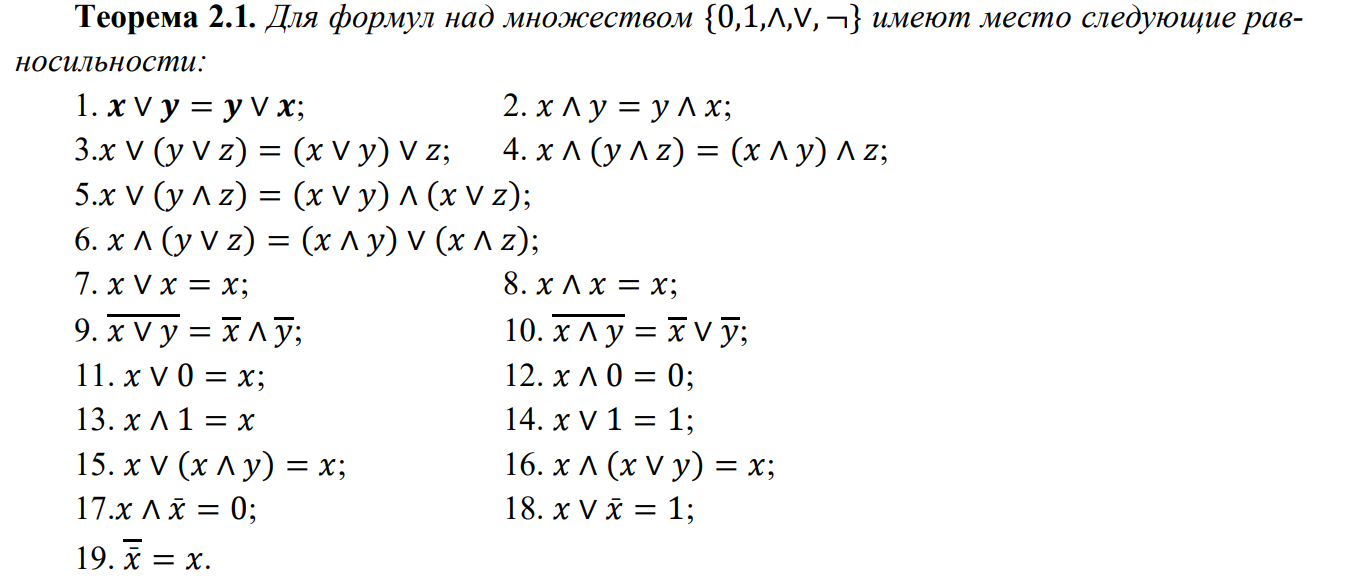
7) Упрощение формул методом равносильных преобразований
Действует принцип: если 𝐴 - подформула формулы 𝛷, то при замене в формуле 𝛷 любого вхождения 𝐴 на равносильную ей формулу 𝐴1 формула 𝛷 переходит в равносильную ей формулу 𝛷1
8) Фиктивные и существенные переменные, равные функции, алгоритм удаления и введения фиктивных переменных
Тема 4. Представление булевых функций формулами специального вида
1) Двойственная функция
2) Принцип двойственности
3) Разложение булевой функции по переменным
4) Совершенная дизъюнктивная нормальная форма (СДНФ)
5) Совершенная конъюнктивная нормальная форма (СКНФ)
6) Представление булевой функции в виде СДНФ и СКНФ
7) Полином Жегалкина, представление булевой функции полиномом Жегалкина
Полиномом Жегалкина над множеством 𝑋 = {𝑥1, 𝑥2, . . . , 𝑥n} называется всякая сумма (по модулю два) различных элементарных конъюнкций над 𝑋, не содержащих отрицаний переменных.
Заметим, что элементарные конъюнкции, не содержащие отрицаний переменных, называют монотонными. Наибольший из рангов элементарных конъюнкций, входящих в полином, называют степенью полинома.
Тема 5. Минимизация дизъюнктивных нормальных форм.
1) Элементарная конъюнкция, ранг элементарной конъюнкции.
2) Дизъюнктивная нормальная форма (ДНФ), сложность ДНФ
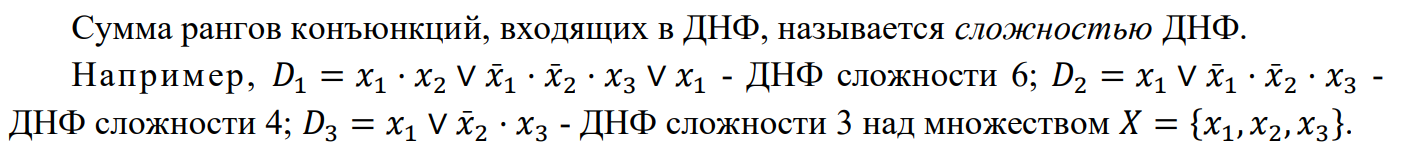
3) Минимальная ДНФ
4) Импликанта, простая импликанта
5) Сокращенная ДНФ
6) Тупиковая ДНФ
Тема 6. Классы Поста и замыкание
1) Функции, сохраняющие 0. Функции, сохраняющие 1
2) Самодвойственные функции
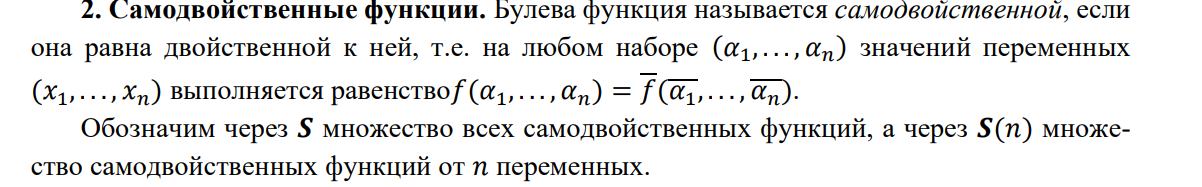
3) Монотонные функции
4) Линейные функции
5) Классы Поста
Множества функций 𝑻𝟎, 𝑻𝟏, 𝑺, 𝑴, 𝑳 называют классами Поста
+ найти полином
6) Замыкание системы булевых функций
Тема 7. Полнота системы булевых функций.
1) Понятие полной системы
2) Теорема о полноте двух систем
3) Лемма о функции, не сохраняющей 0. Лемма о функции, не сохраняющей 1
4) Лемма о несамодвойственной функции. Лемма о немонотонной функции
5) Лемма о нелинейной функции
6) Критерий полноты системы булевых функций (теорема Поста)
7) Базисы
Тема 8. Неориентированные графы: первичные понятия
1) Граф, его вершины и ребра
2) Смежные вершины, Кратные ребра, петли, Инцидентные вершины и ребра
3) Степени вершин, Висячие и изолированные вершины
4) Лемма о рукопожатиях
5) Диаграмма графа
6) Изоморфные графы
7) Специальные виды графов: обыкновенные, полные, двудольные, полные двудольные графы
Обыкновенный
Граф без петель и кратных ребер называется обыкновенным.
Полный
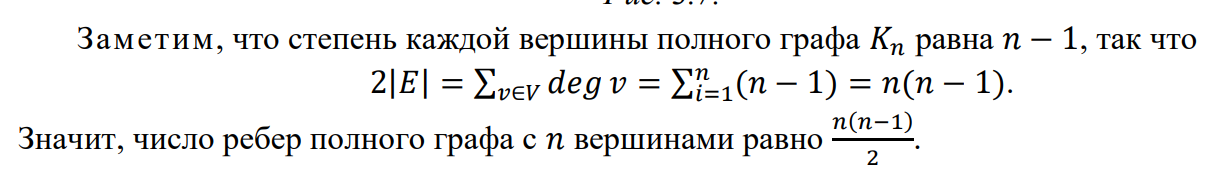
Двудольный
Двудольным графом называется обыкновенный граф, множество вершин которого может быть разбито на два непустых непересекающихся подмножества (доли), так что концы каждого ребра графа принадлежат разным долям.
Двудольный граф называется полным двудольным графом, если любые две его вершины, принадлежащие разным долям, смежные.
8) Матрица смежности и матрица инцидентности
9) Подграфы и операции над ними
