Лабки-лапки / LR3-Tomozov-Slastin

МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

Кафедра КСУ

ОТЧЕТ

по лабораторной работе № 3

по дисциплине «Моделирование систем управления»

Тема: ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ ДИНАМИЧЕСКОЙ СИСТЕМЫ

Вариант 2

Студенты гр. 1487		Томозов Г. Н. Сластин Н. Ю.
Преподаватель		Лукомская О. Ю.

Санкт-Петербург

2025

Цель работы: Исследовать переходные процессы, происходящие в динамической системе на примере ГПТ НВ.

Исходные данные:

ГПТ НВ, работающий на сеть большой мощности

U_ВН = 220 В, U_СH = 220 B, M_ВH = 70 Нм, i_H = 50 A, ω_н = 100 с^-1, С_М = 200, С_{Е =} 205_, J=0.35 кг*м², L_Я = 0.01 Гн, r_B = 145 Ом, r_Я = 0.3 Ом, Фн = 0.007 Вб, w = 4000 витков.

Аппроксимирующий полином (из Л.Р. №1):

p = [ 1.1348 , 0 , 1.2877, 0, 1.7620, 0];

Уравнения, описывающие ГПТ:

.

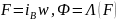
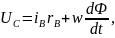
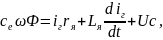
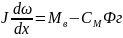Вектор переменных и вектор входов:

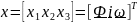- вектор переменных

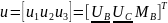– вектор входов

Нормирование параметров:

Нормированные значения могут быть вычислены по формулам.

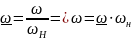
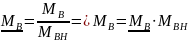
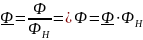
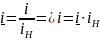
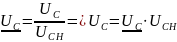
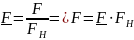
Кроме того выразим ток возбуждения через МДС:

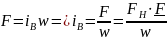
Из л.р.№1 известно, что =

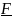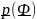
C учетом вышенаписанного исходные уравнения принимают вид:

В

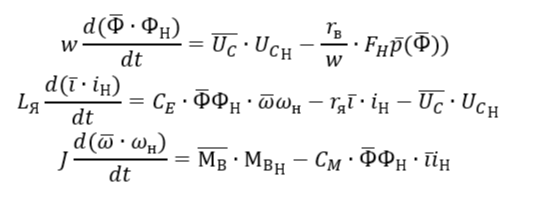
Далее с учётом вектора переменных и вектора входа можно перейти к описанию СНДУ в унифицированном виде (без учета выхода):

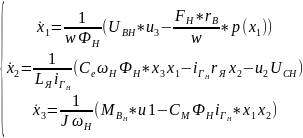
Параметры для нашей модели:

J = 0.12;

wn = 100;

Cm = 200;

potokn = 0.005;

In = 50;

Mvn = 70;

Lya=0.01;

Ucn = 220;

Uvn = 220;

Ce = 205;

ra = 0.3;

w = 4000;

rb = 145;

rv = 145;

Fn = (Ucn*w)/rv;

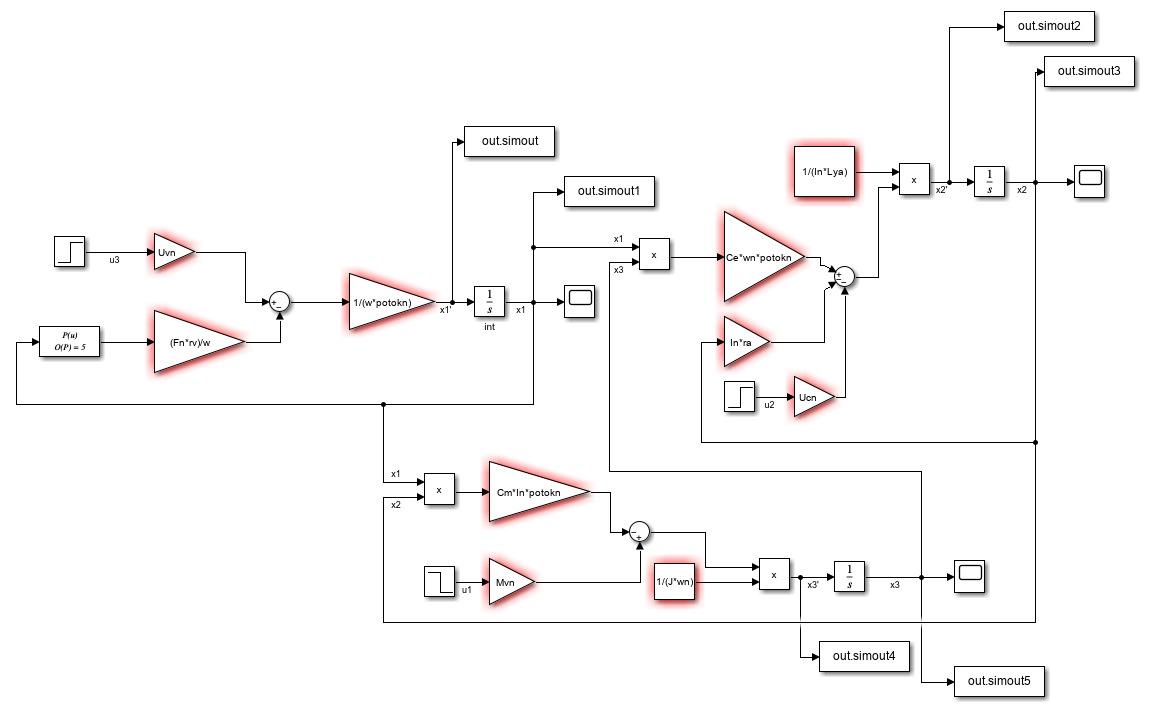
Рисунок 1 - Сборка Simulink модели

В итоге получаем следующие переходные характеристики и фазовые портреты:

При номинальных значениях

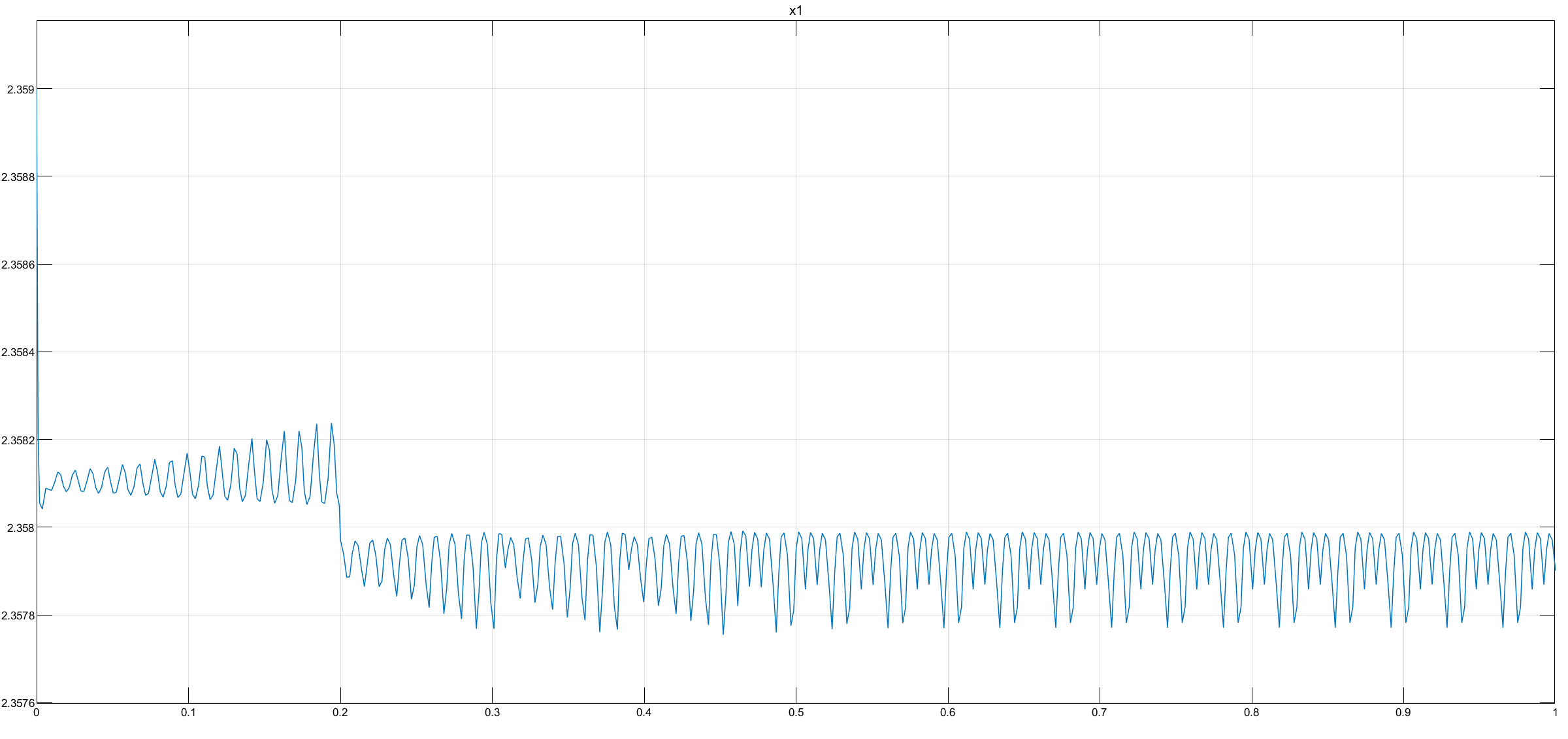
Рис.2 - Переходная характеристика Uvn

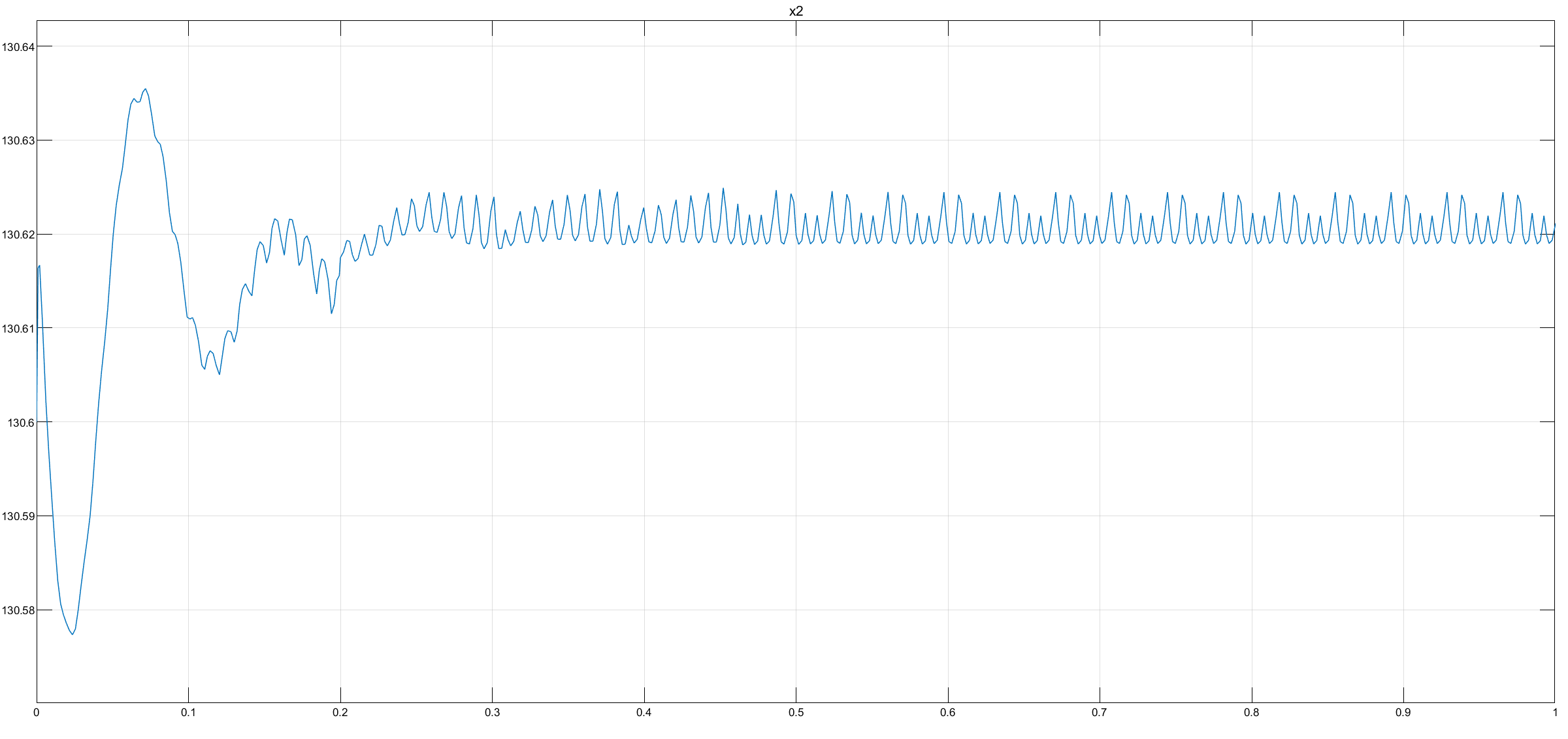
Рис.3 - Переходная характеристика Ucn

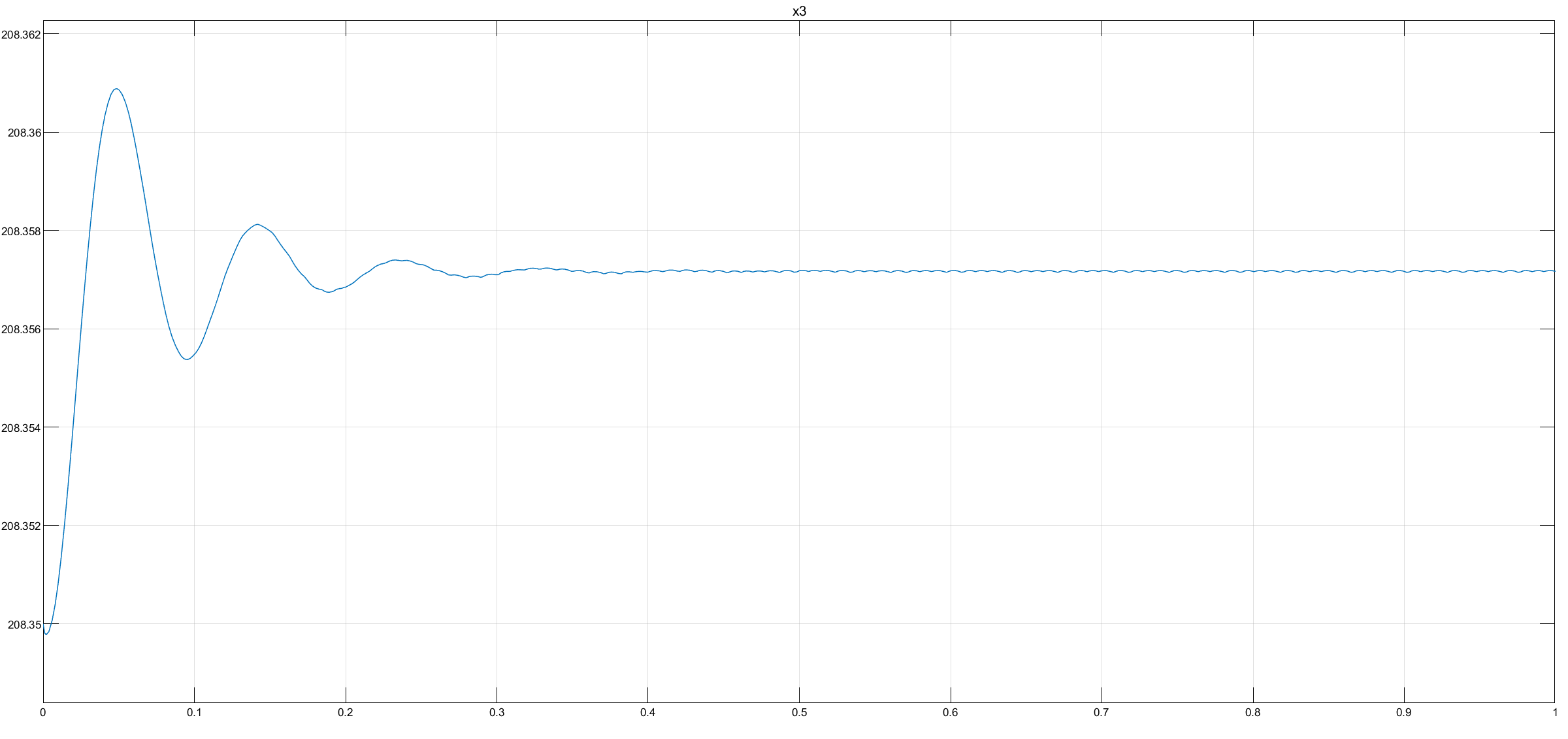
Рис. 4 - Переходная характеристика Mvn

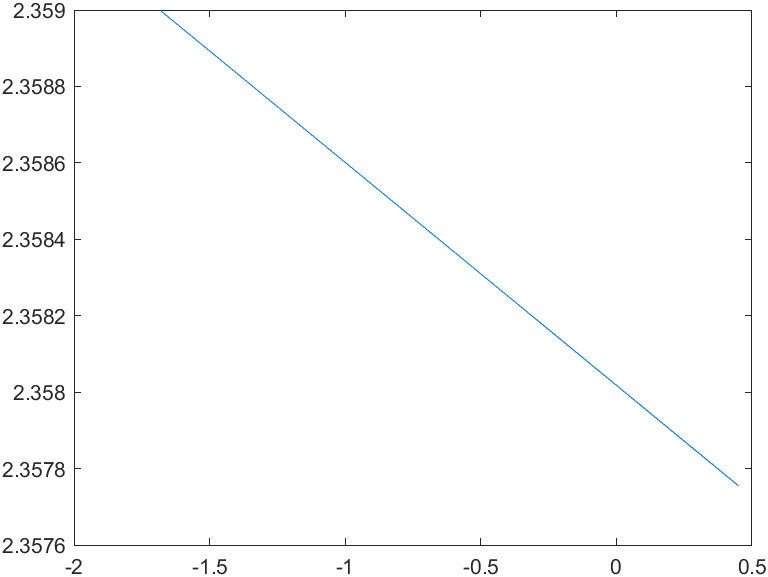
Рис. 5 - Фазовый портрет Uvn

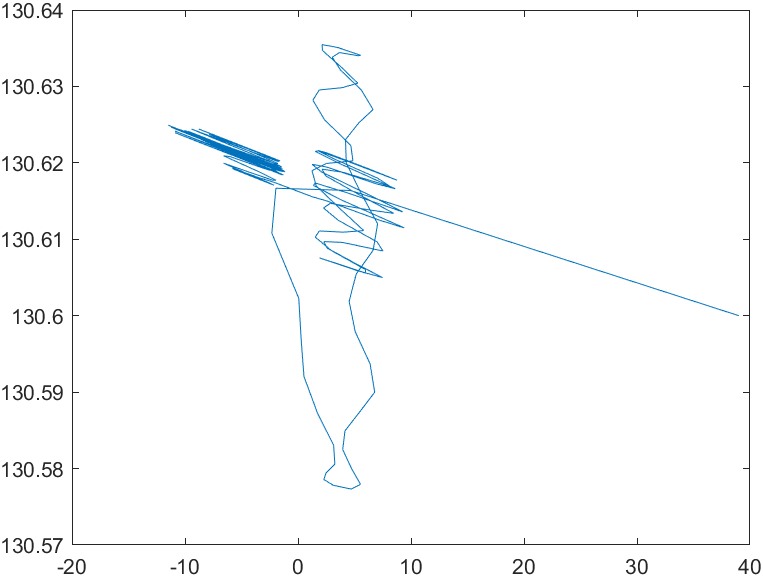
Рис. 6 - Фазовый портрет Ucn

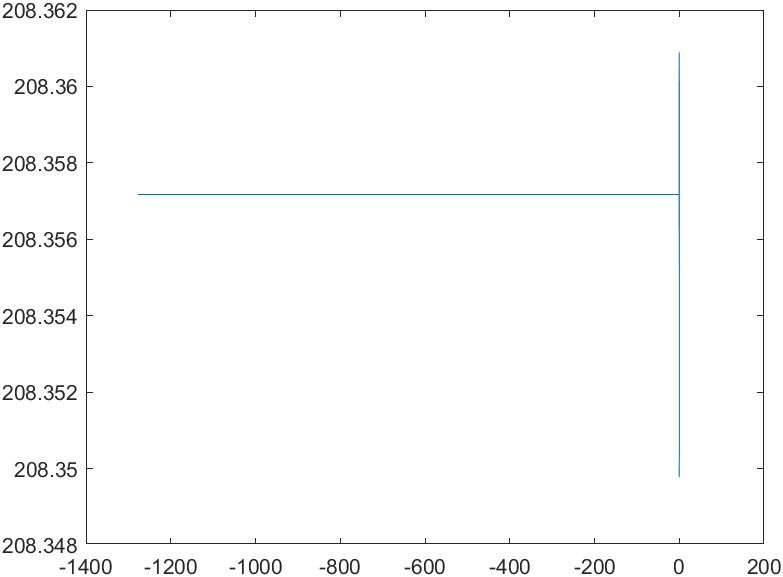
Рис. 7 - Фазовый портрет Mvn

Увеличиваем параметр Uvn на 40%:

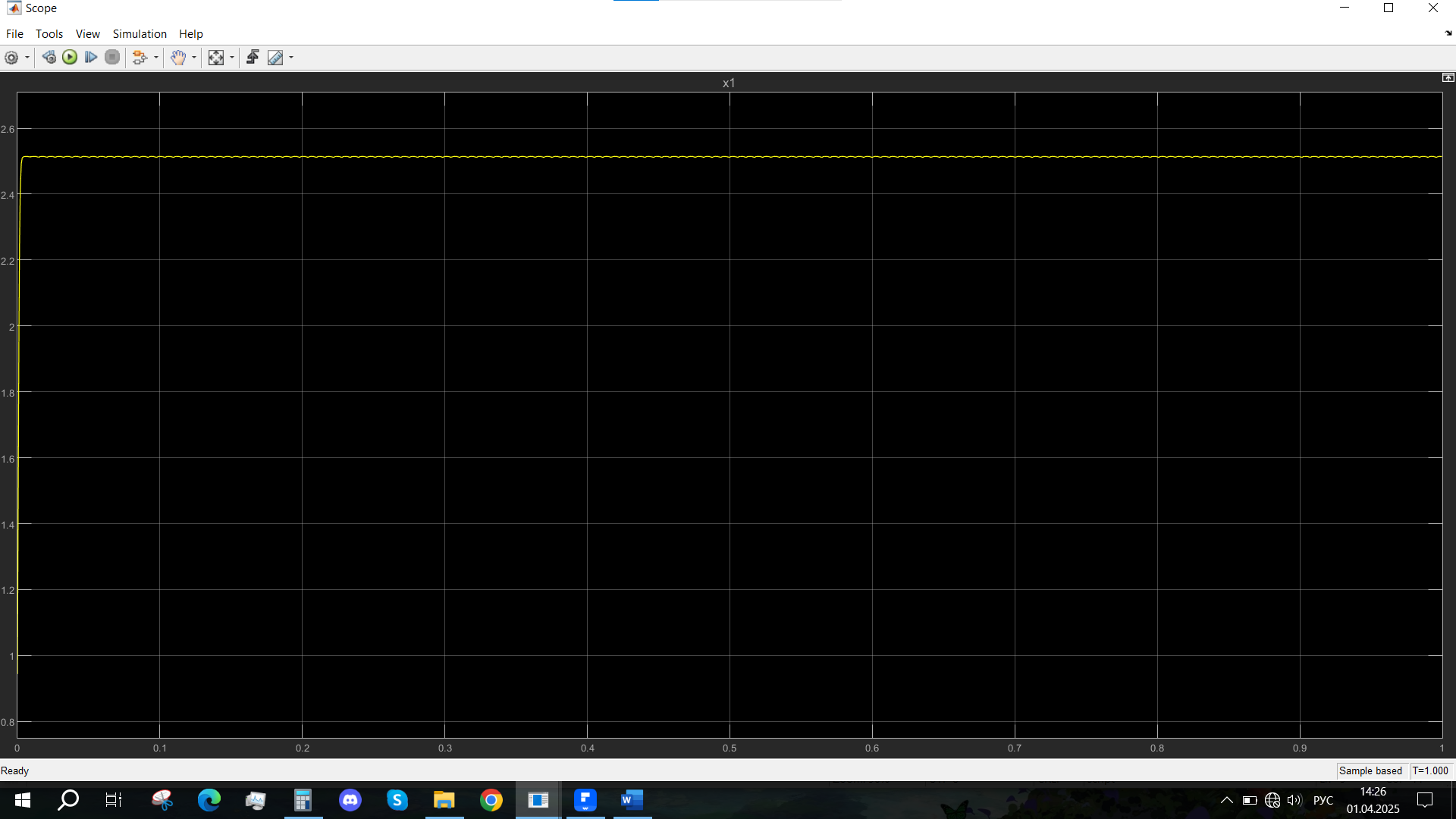
Рис.8 - Переходная характеристика Uvn

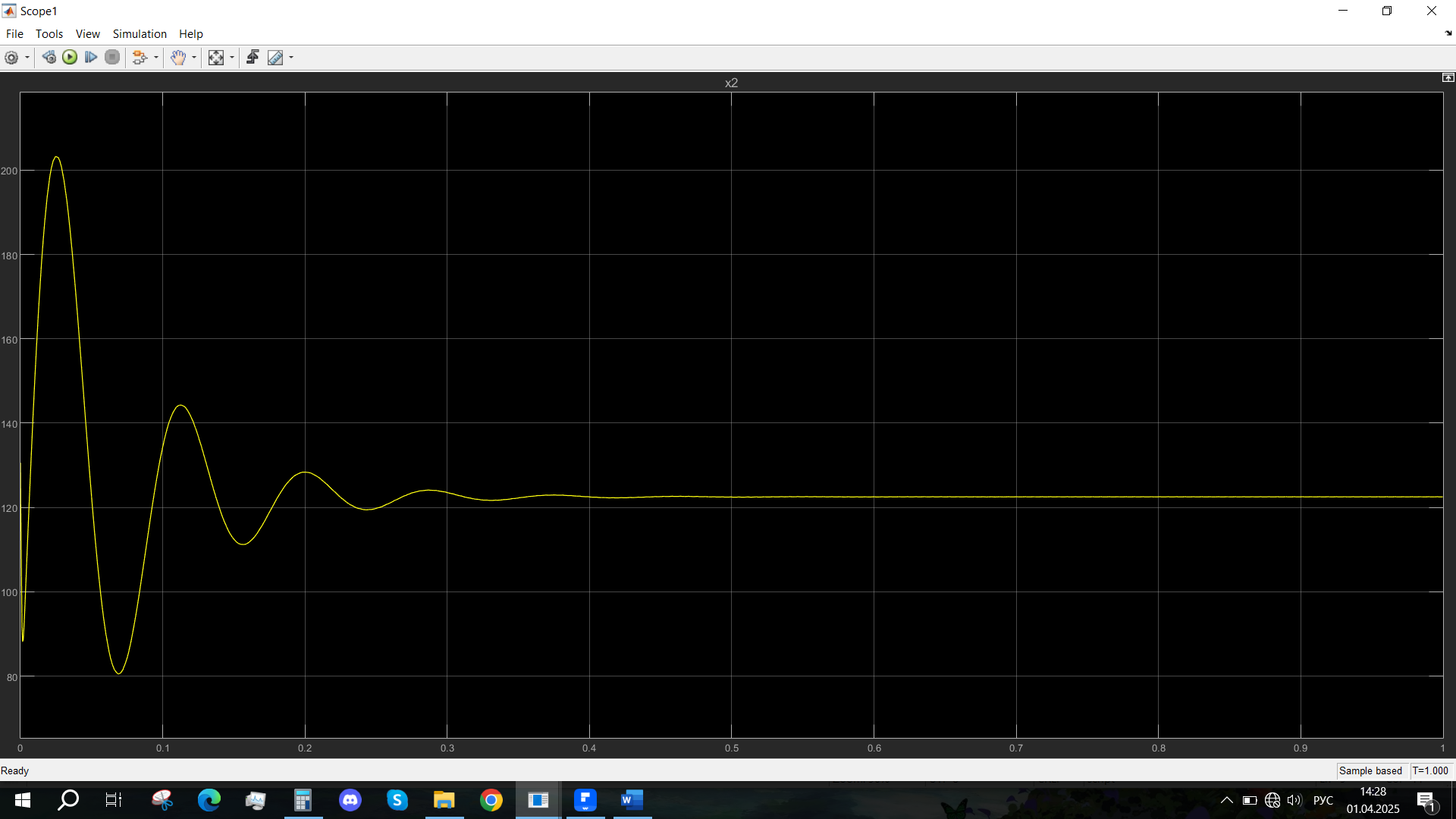
Рис.9 - Переходная характеристика Ucn

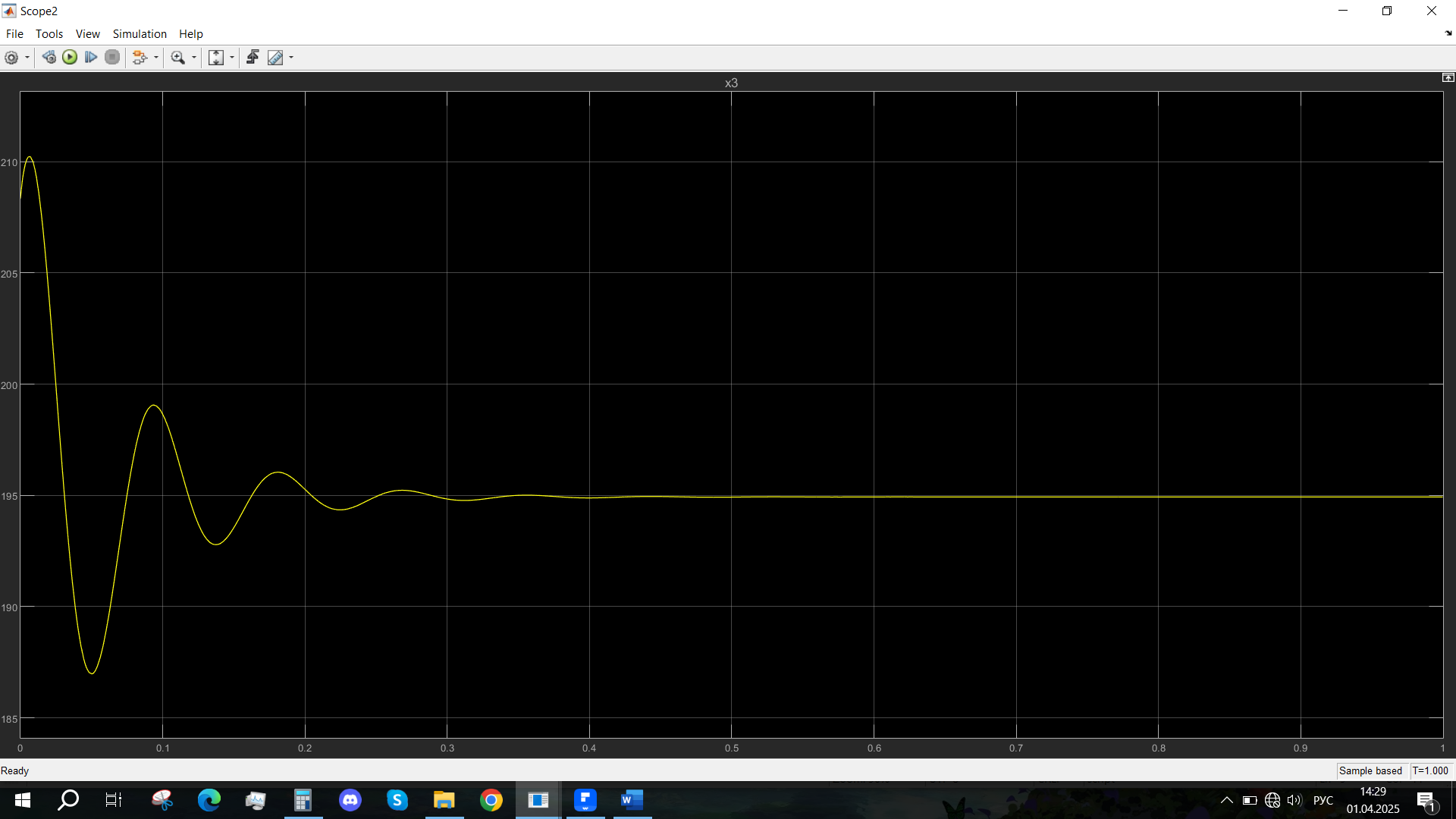
Рис. 10 - Переходная характеристика Mvn

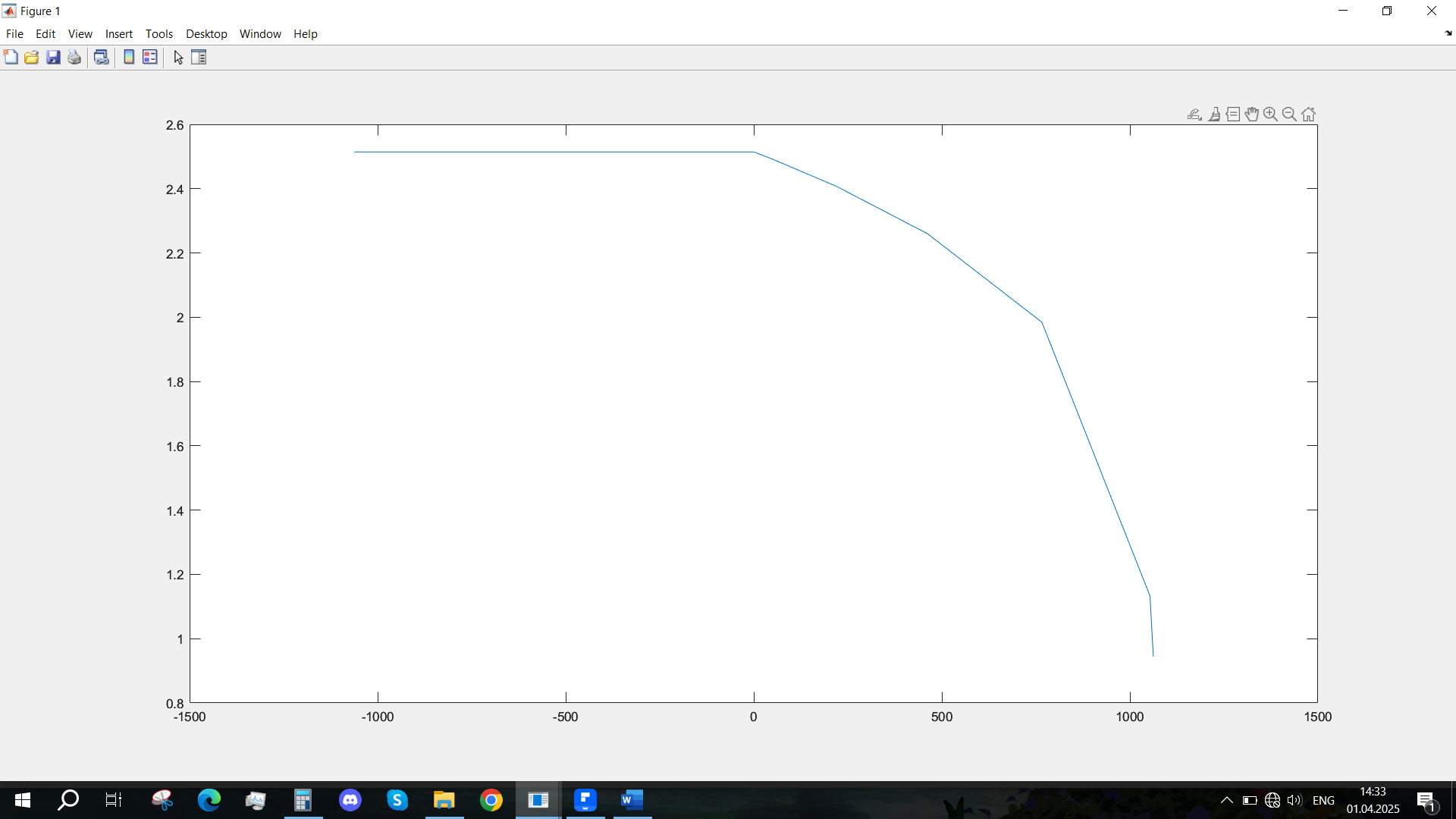
Рис. 11 - Фазовый портрет Uvn

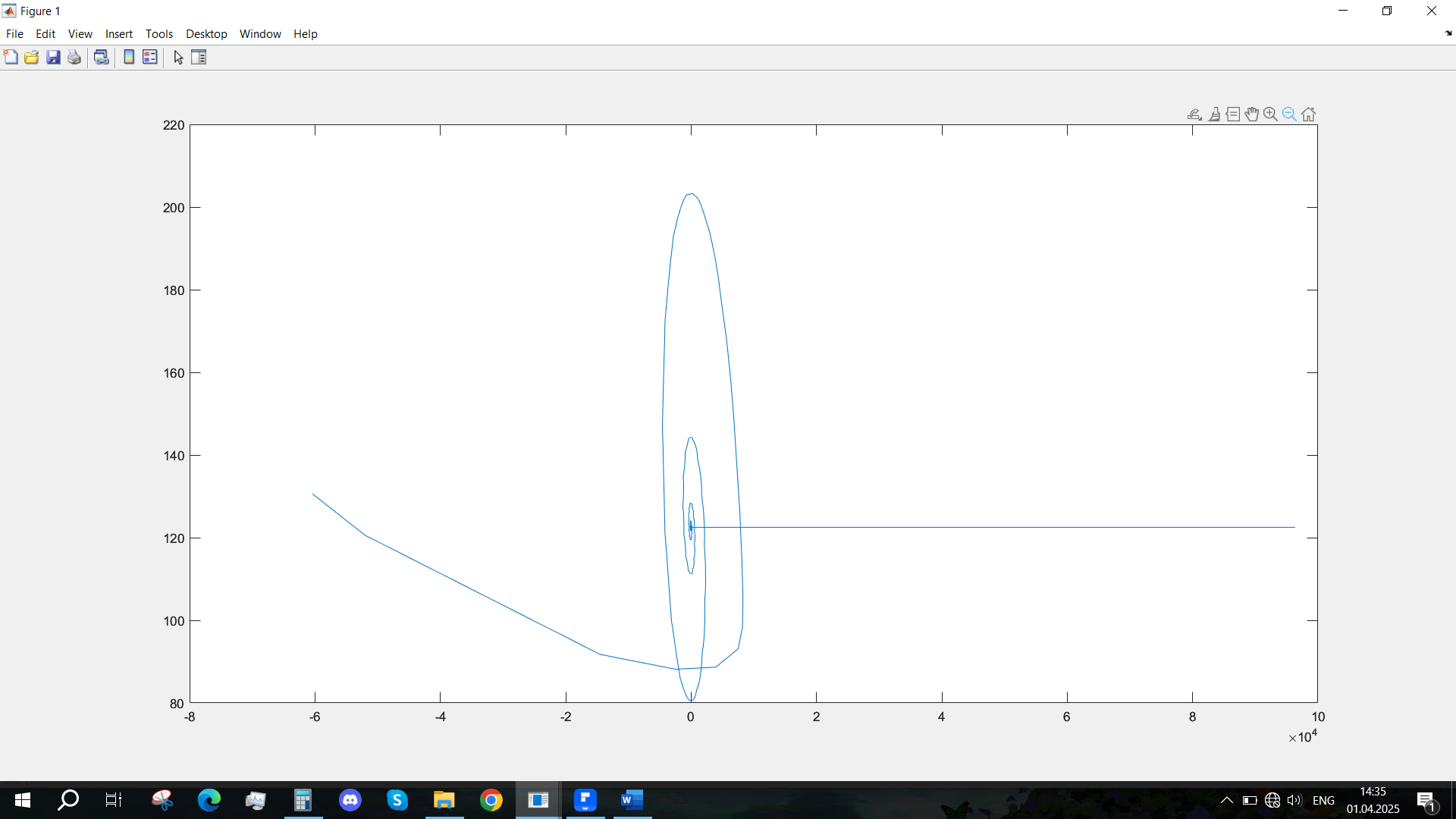
Рис. 12 - Фазовый портрет Ucn

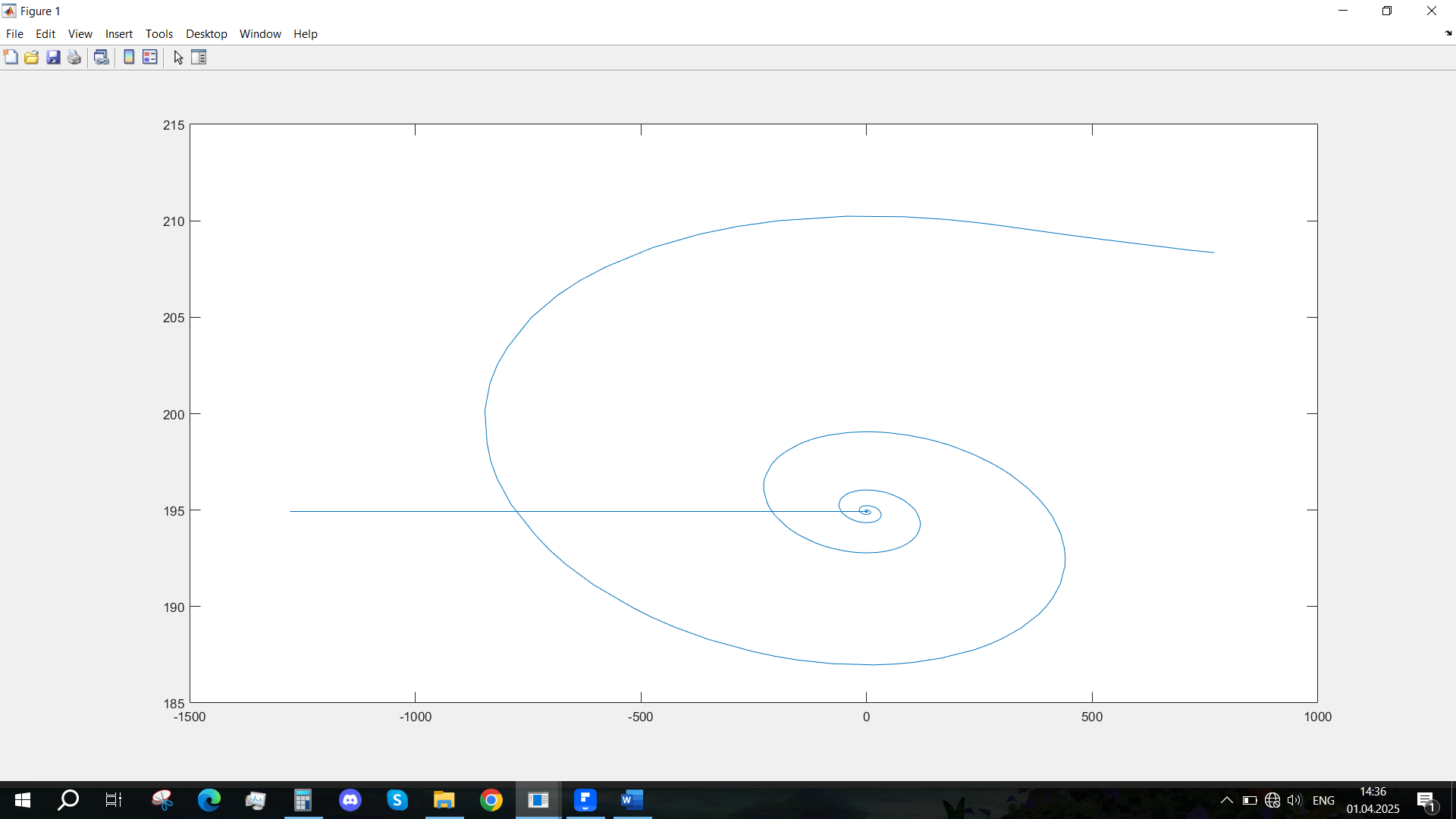
Рис. 13 - Фазовый портрет Mvn

Теперь увеличиваем Uvn на 60%

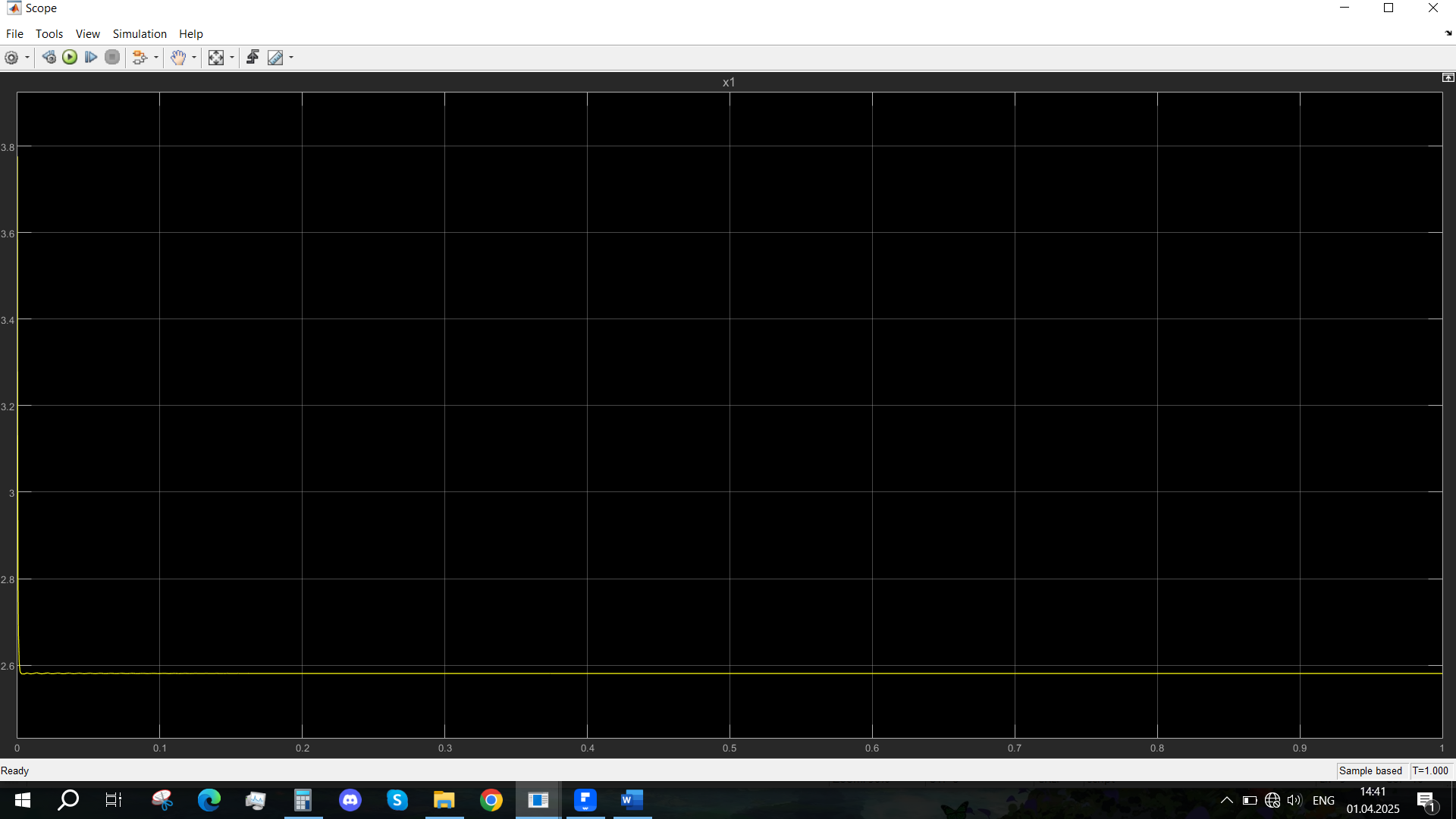
Рис. 14 - Переходная характеристика Uvn

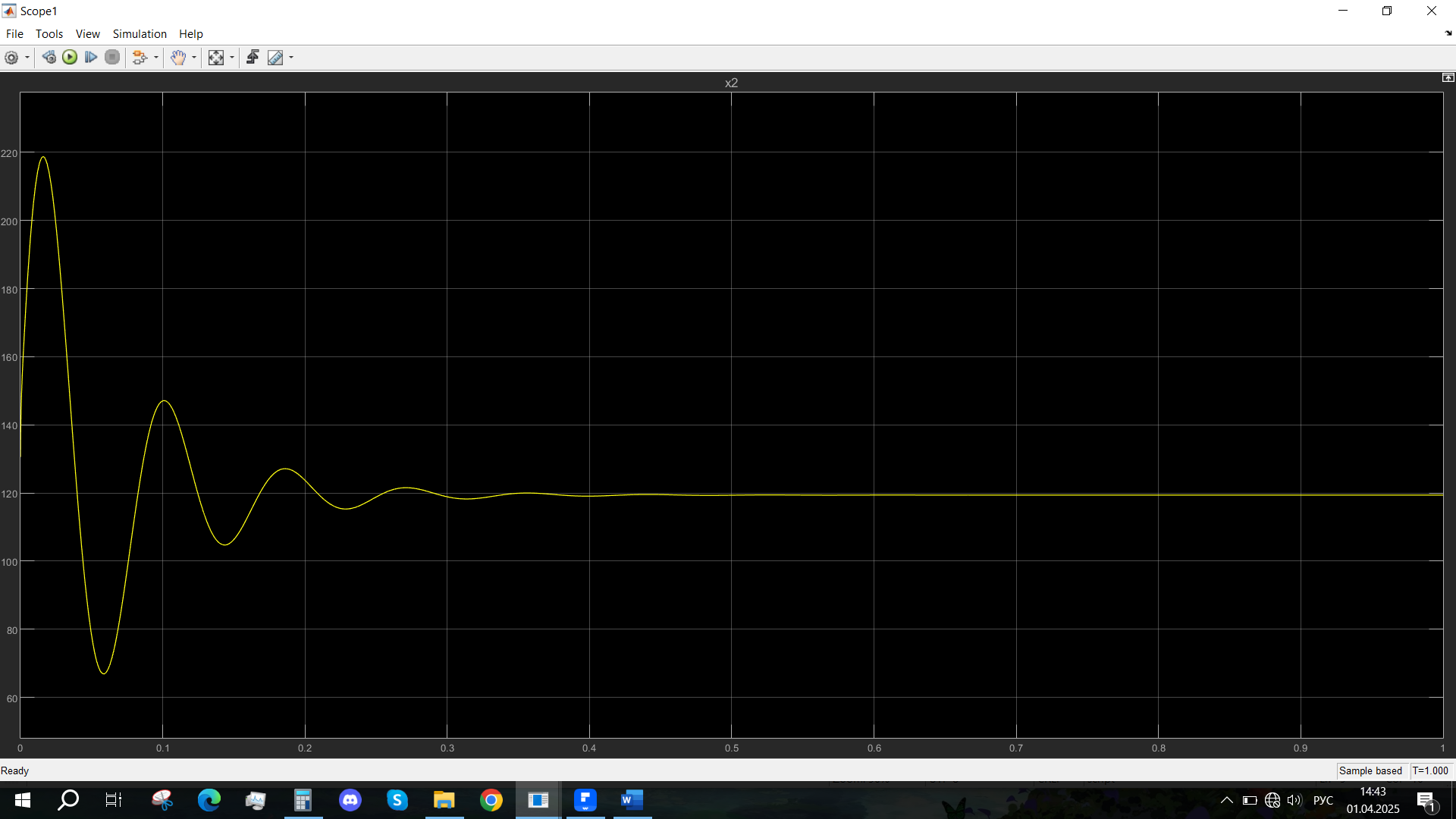
Рис. 15 - Переходная характеристика Uсn

Рис. 16 - Переходная характеристика Mvn

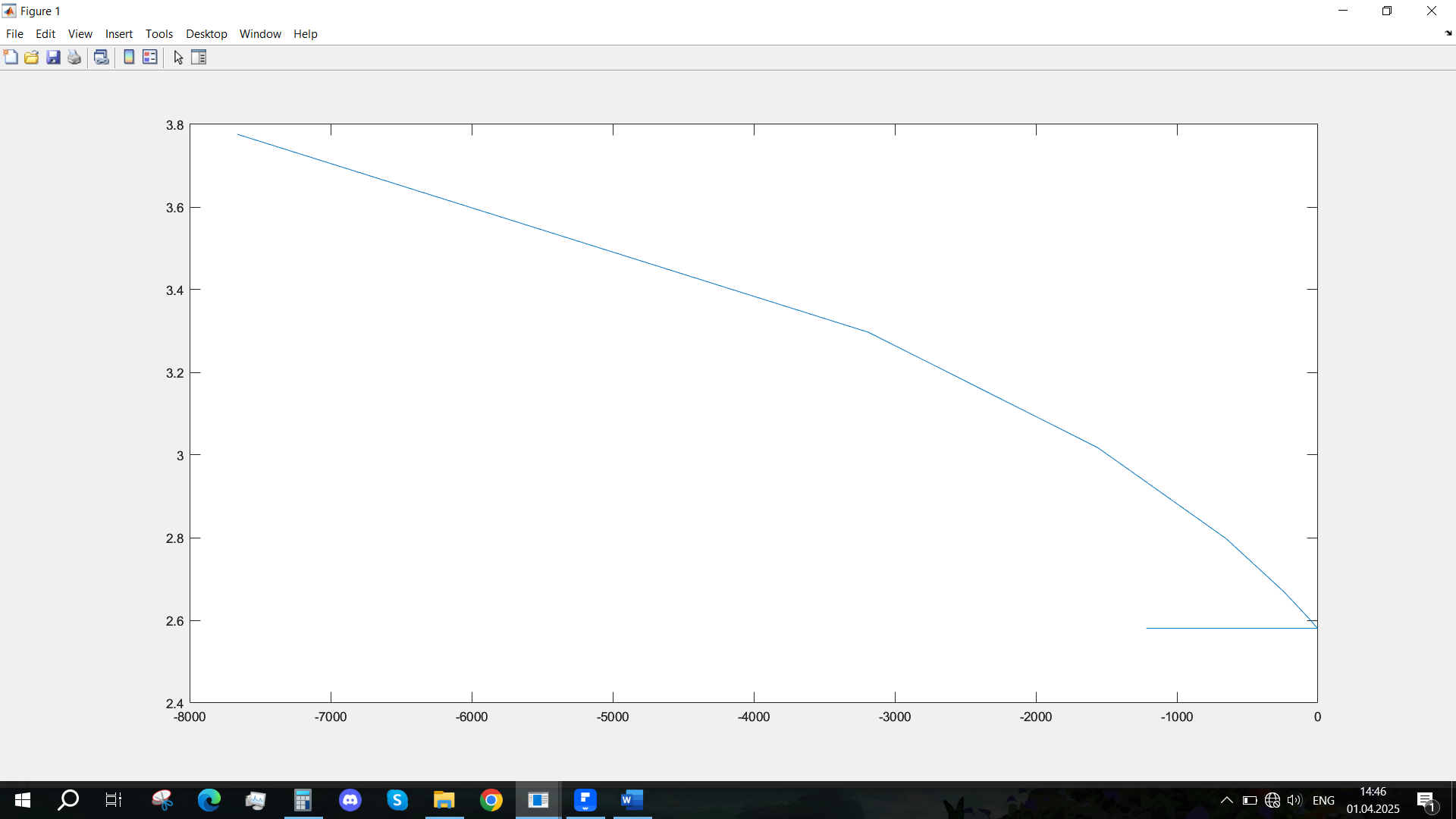
Рис. 17 - Фазовый портрет Uvn

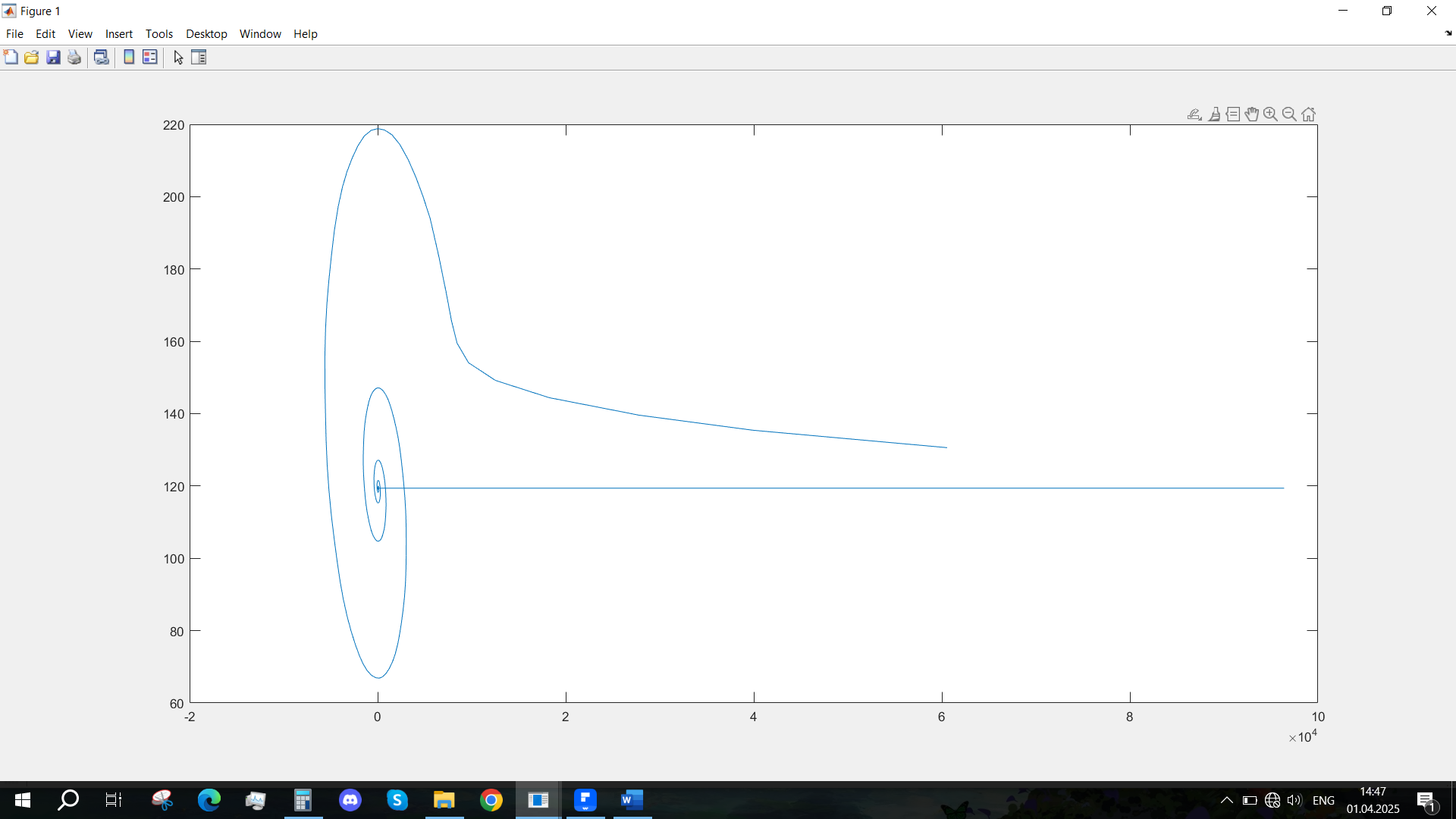
Рис. 18 - Фазовый портрет Ucn

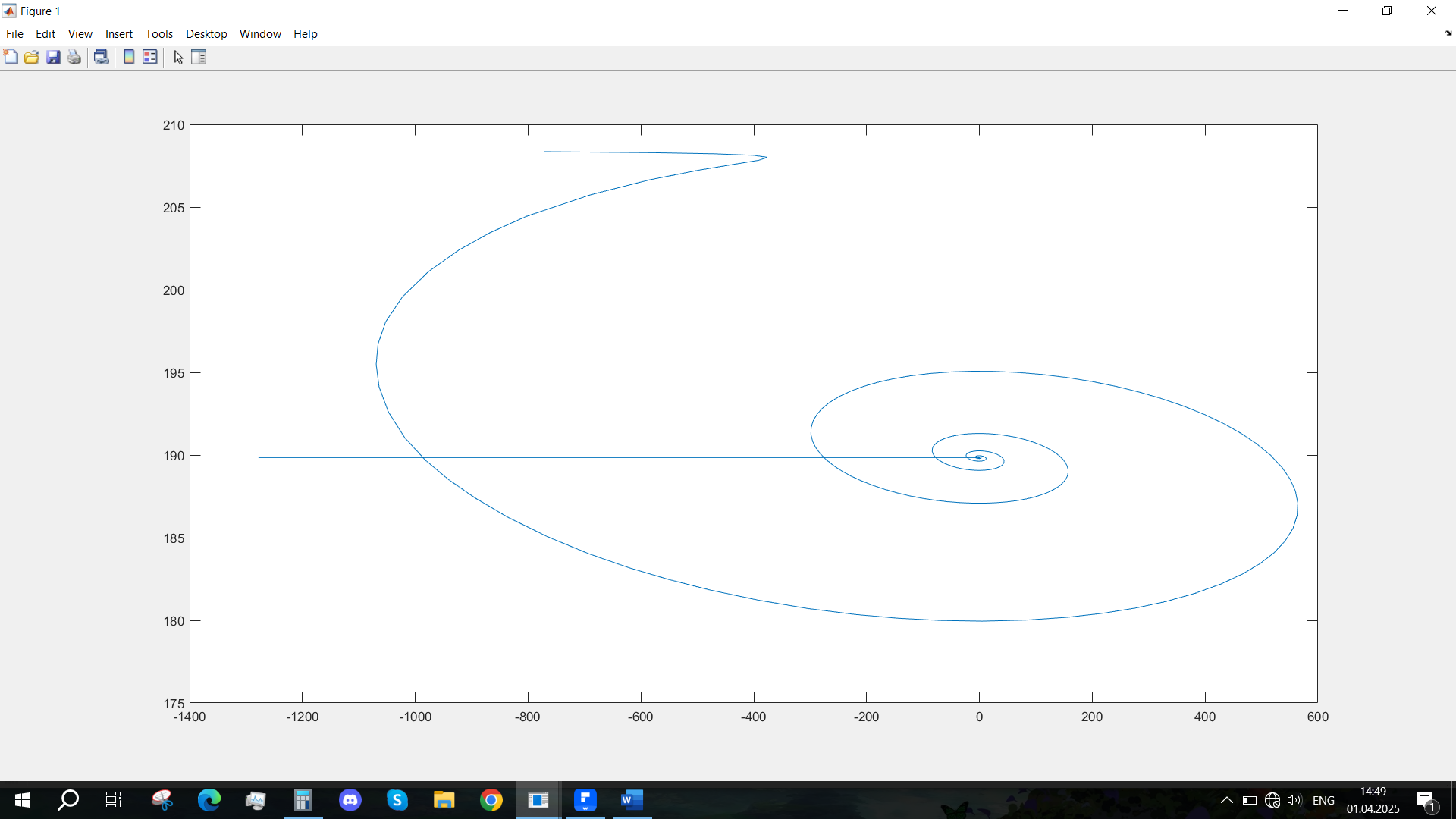
Рис. 19 - Фазовый портрет Mvn

Меняем Ucn на 40%

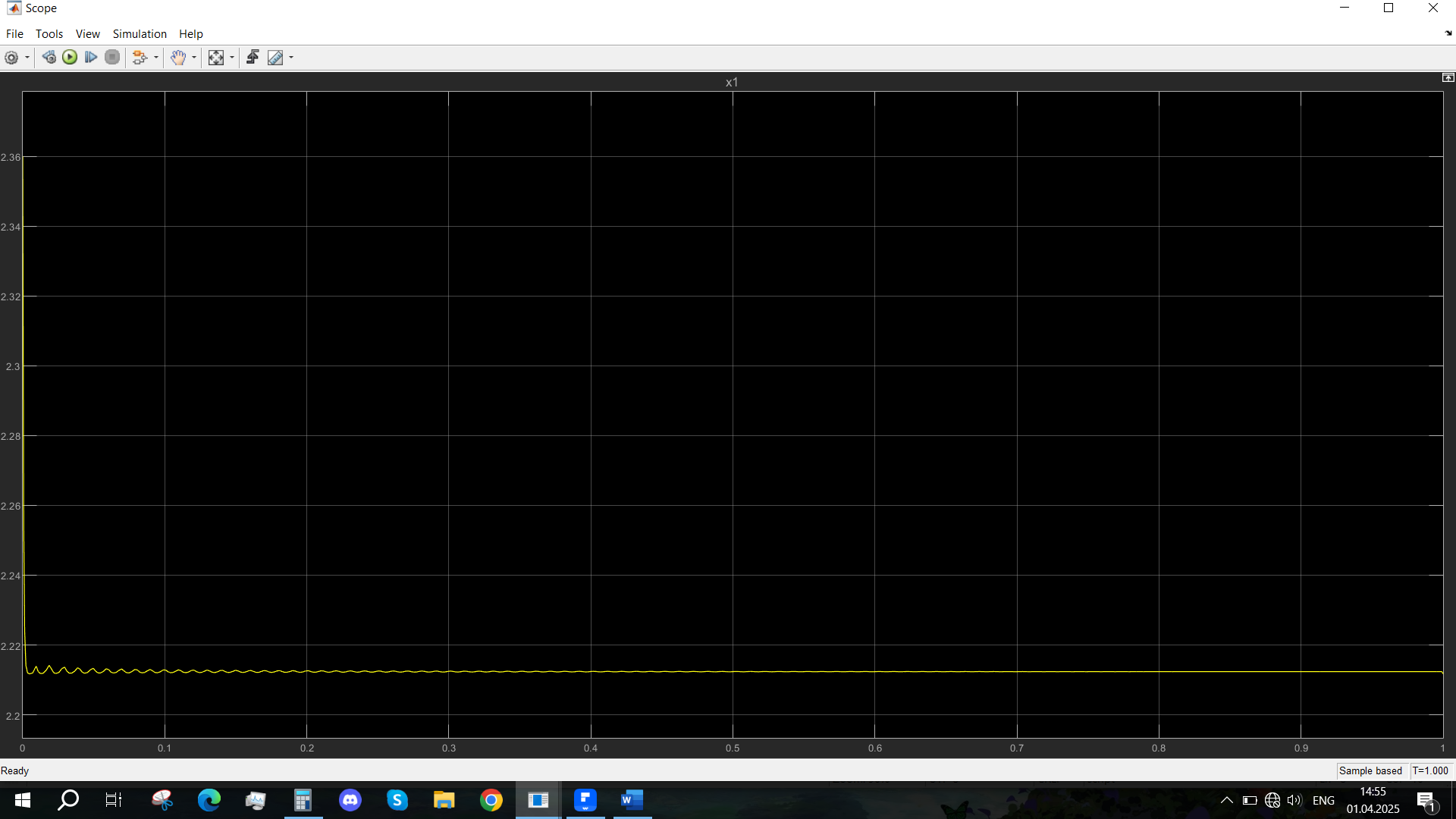
Рис. 20 - Переходная характеристика Uvn

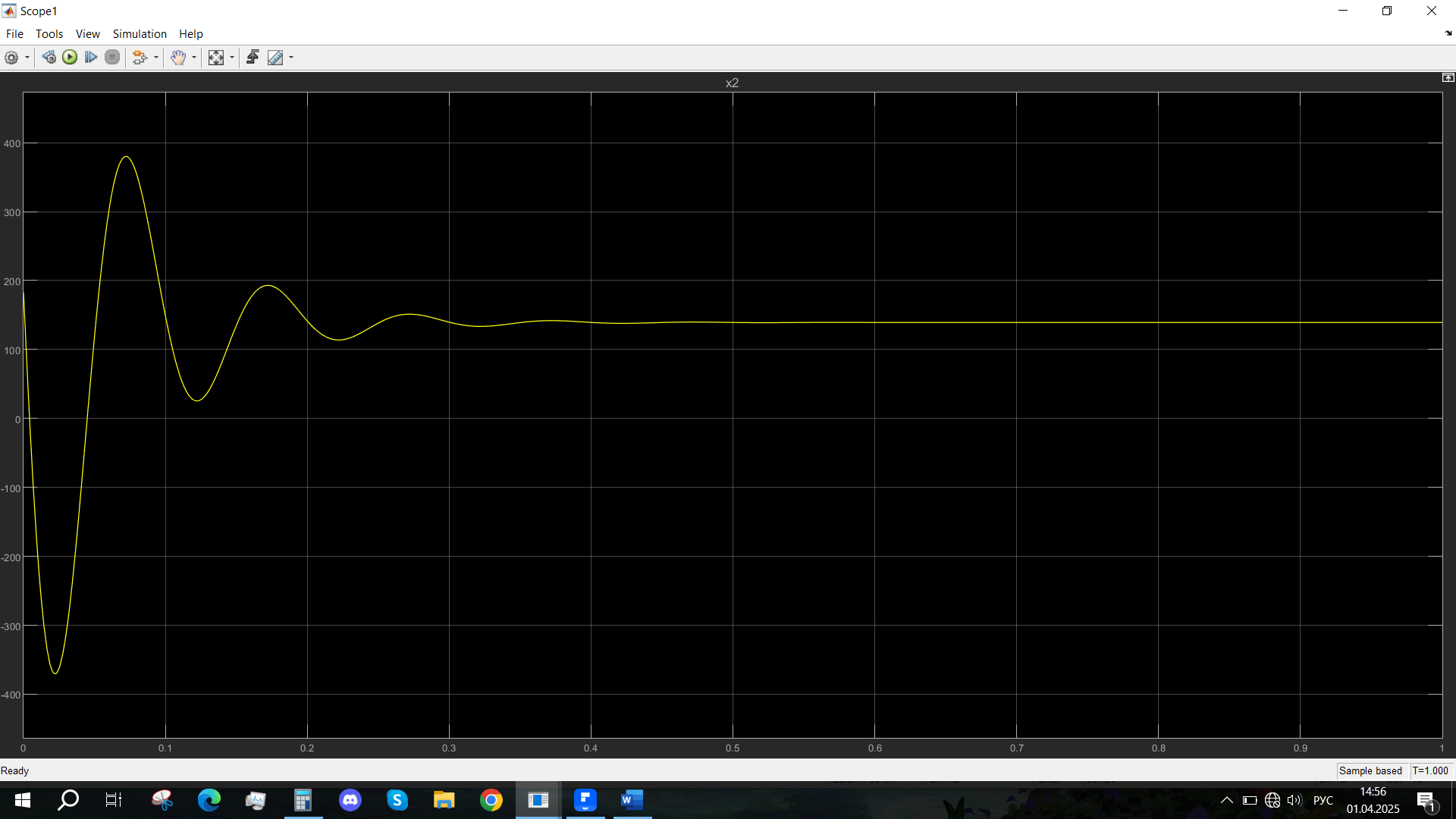
Рис. 21 - Переходная характеристика Ucn

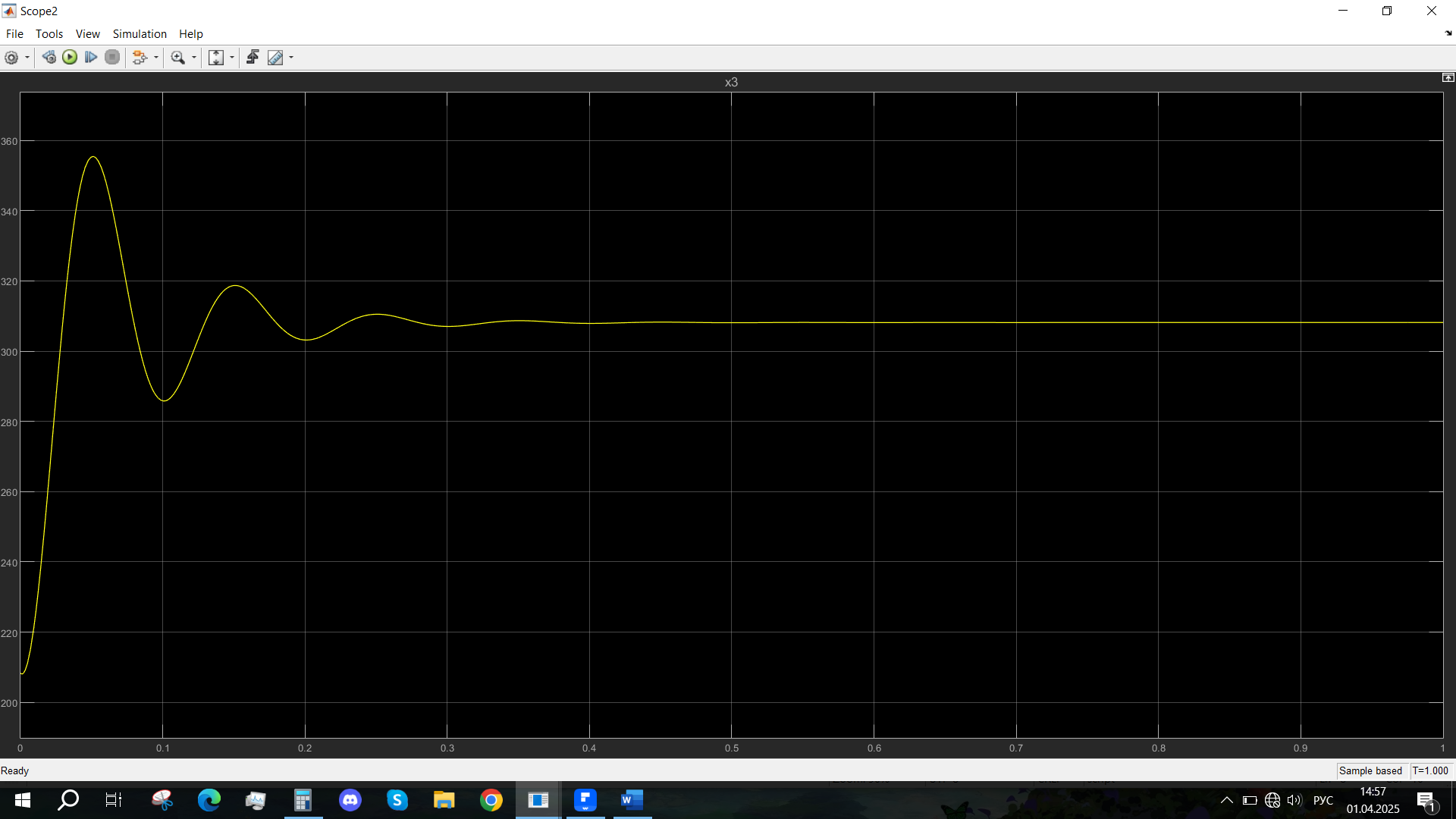
Рис. 22 - Переходная характеристика Mvn

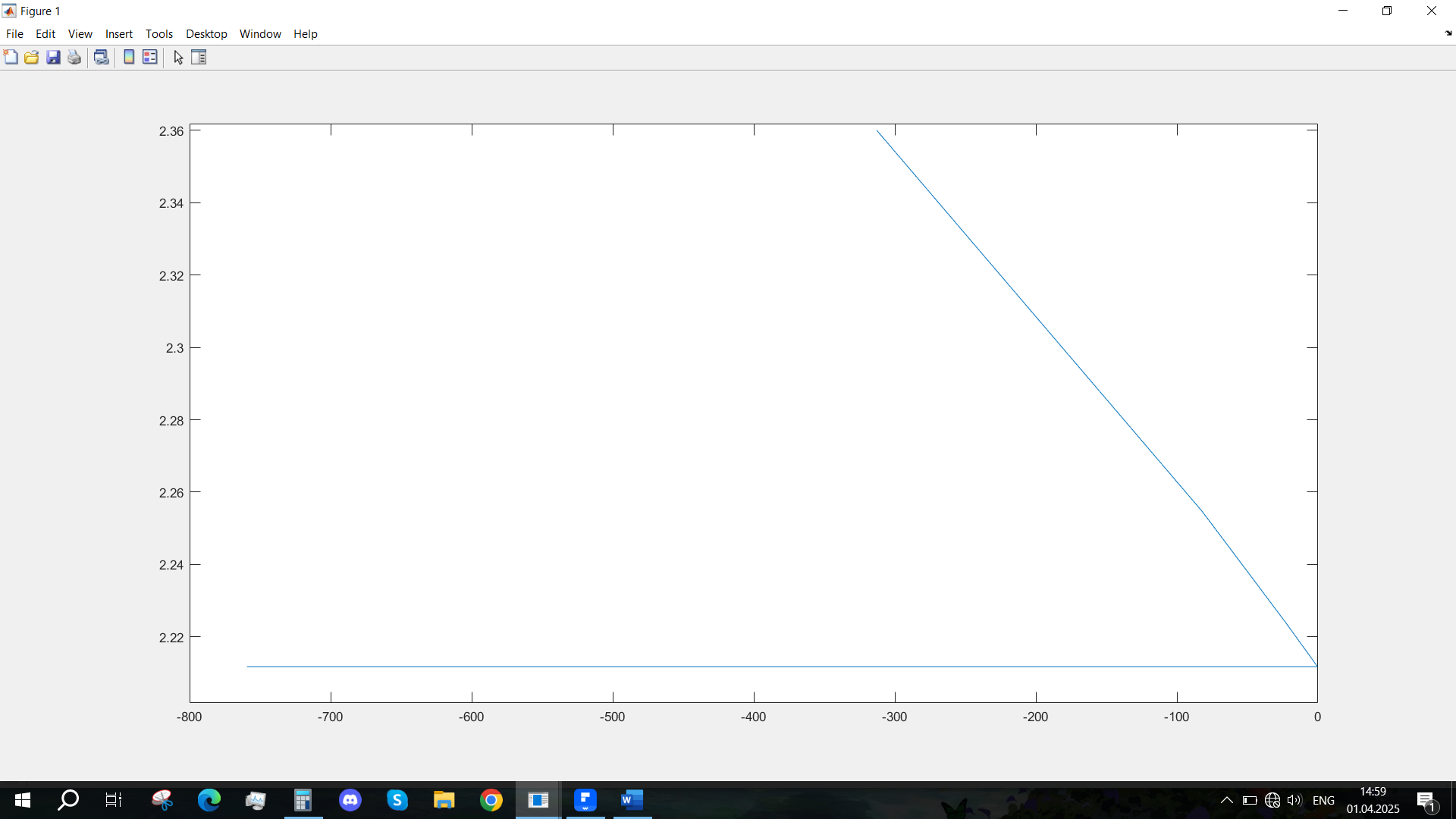
Рис. 23 - Фазовый портрет Uvn

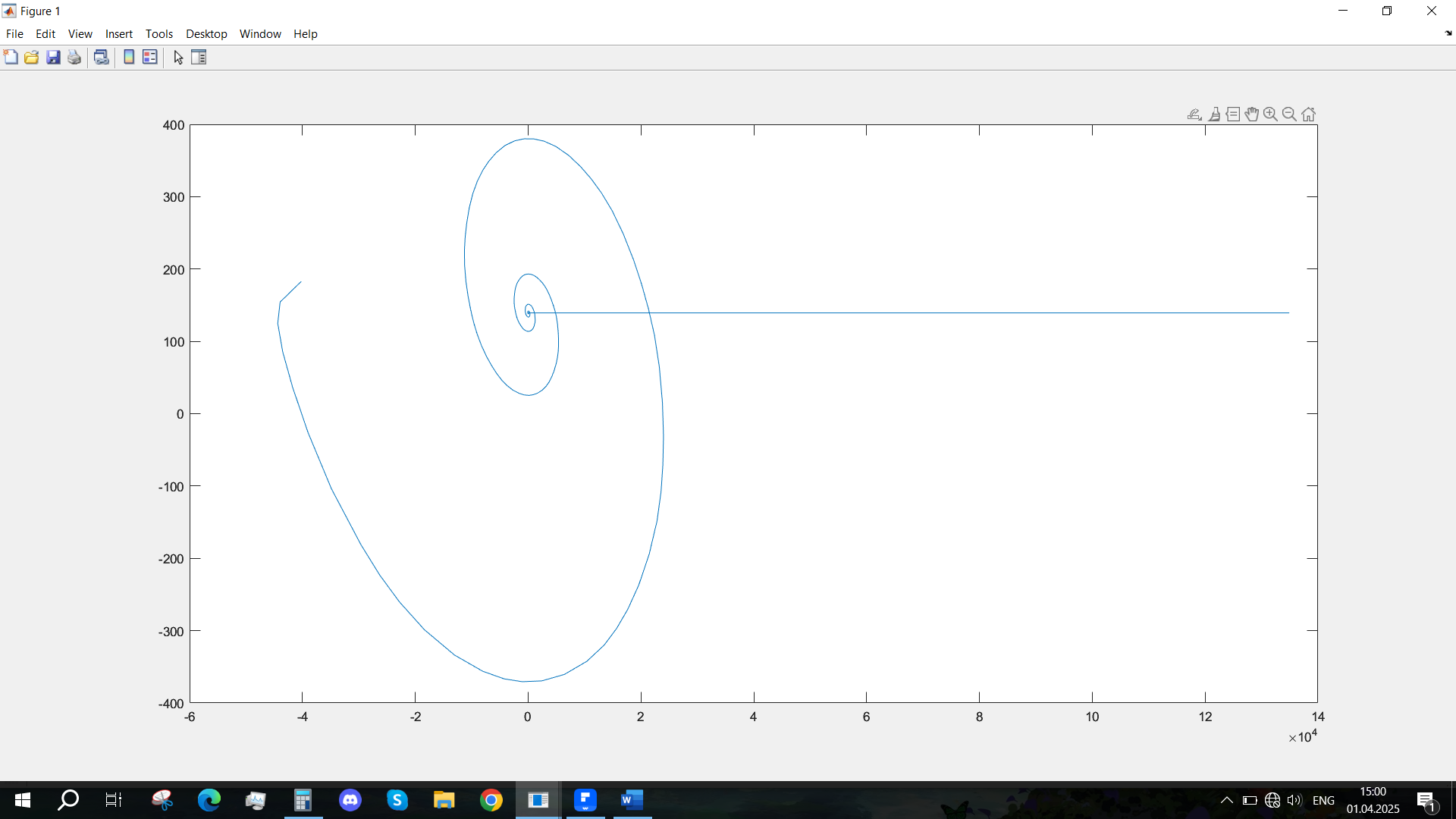
Рис. 24 - Фазовый портрет Ucn

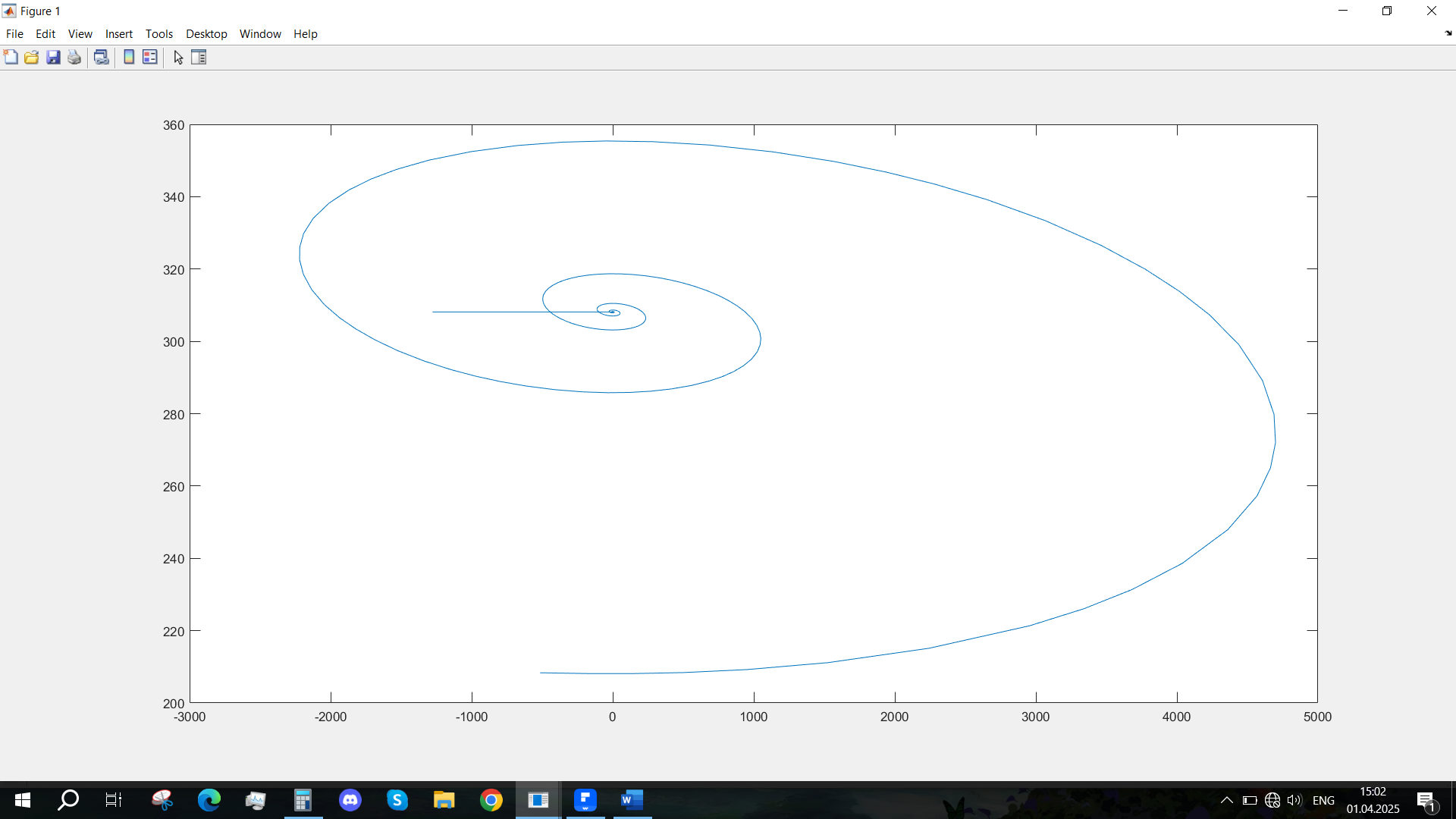
Рис. 25 - Фазовый портрет Mvn

меняем на 60%

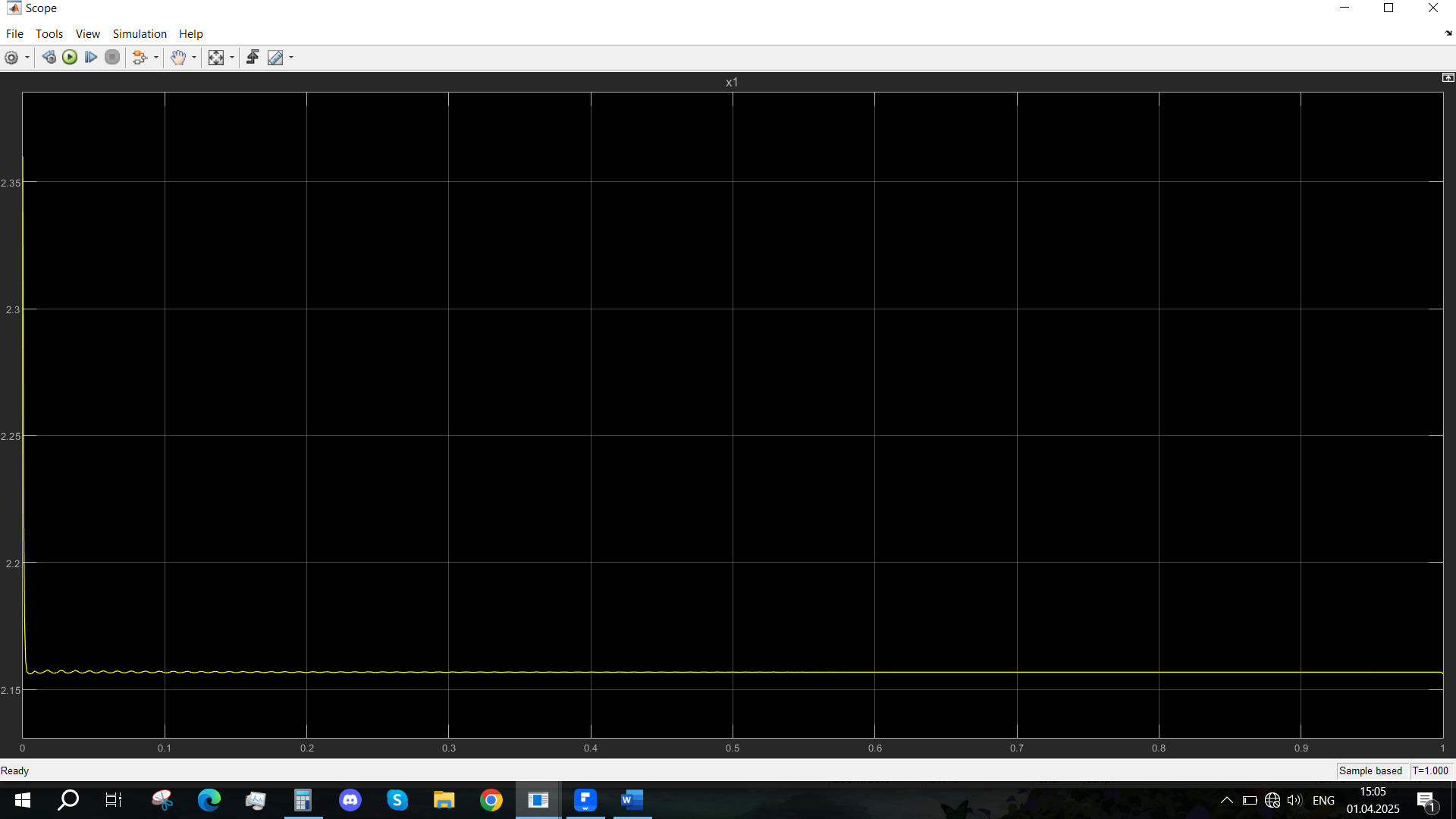
Рис. 26 - Переходная характеристика Uvn

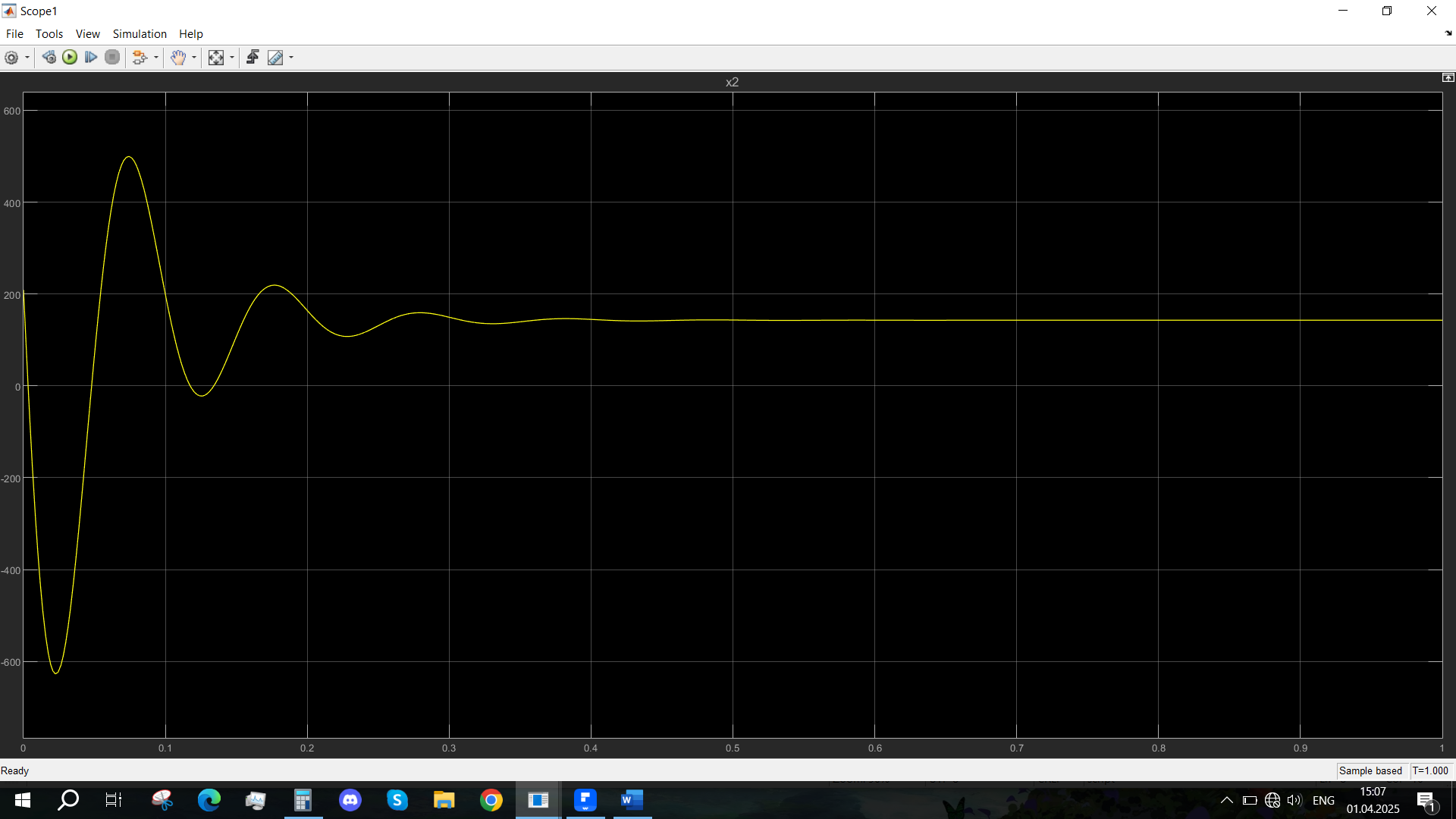
Рис. 27 - Переходная характеристика Ucn

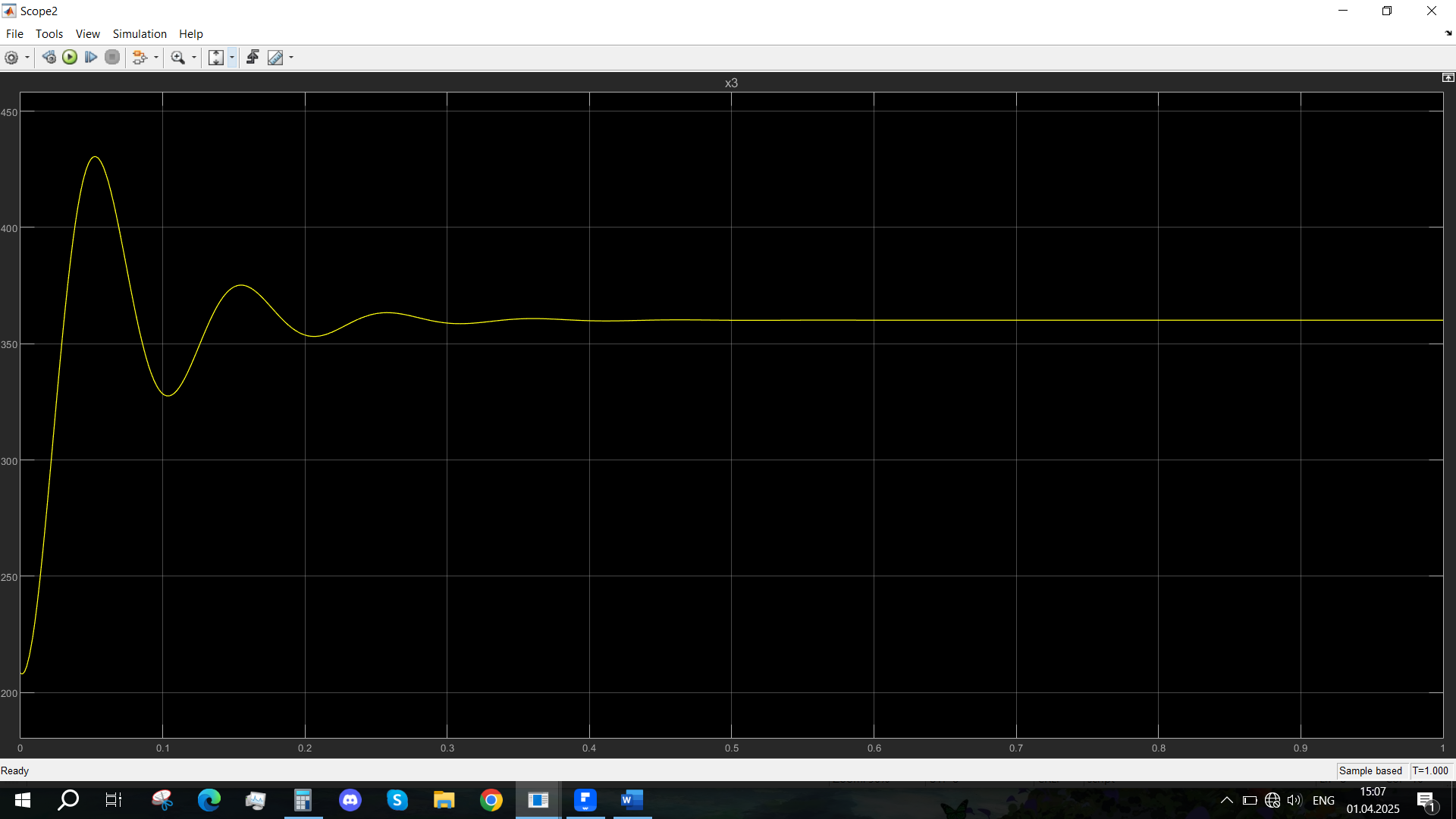
Рис. 28 - Переходная характеристика Mvn

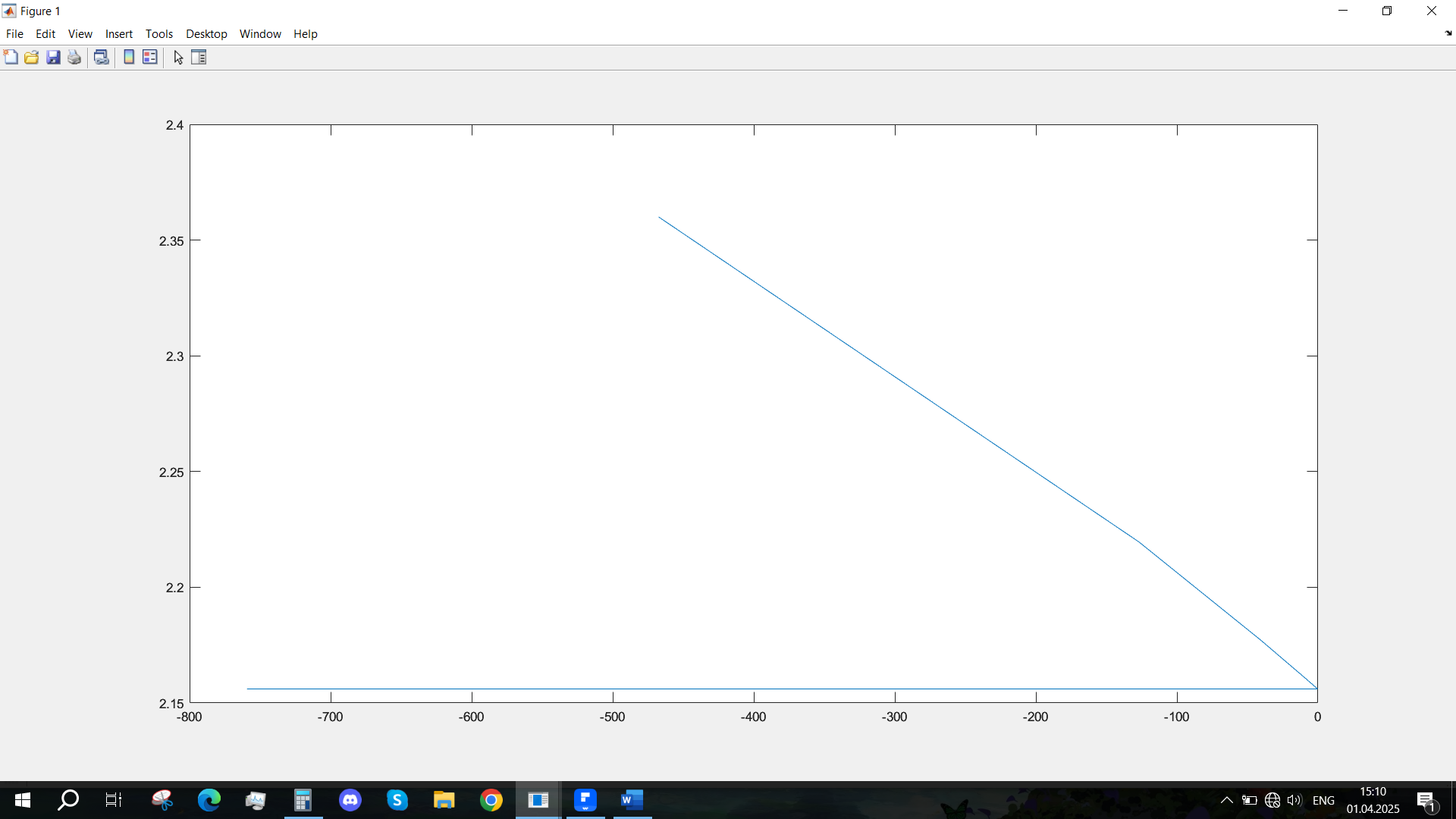
Рис. 29 - Фазовый портрет Uvn

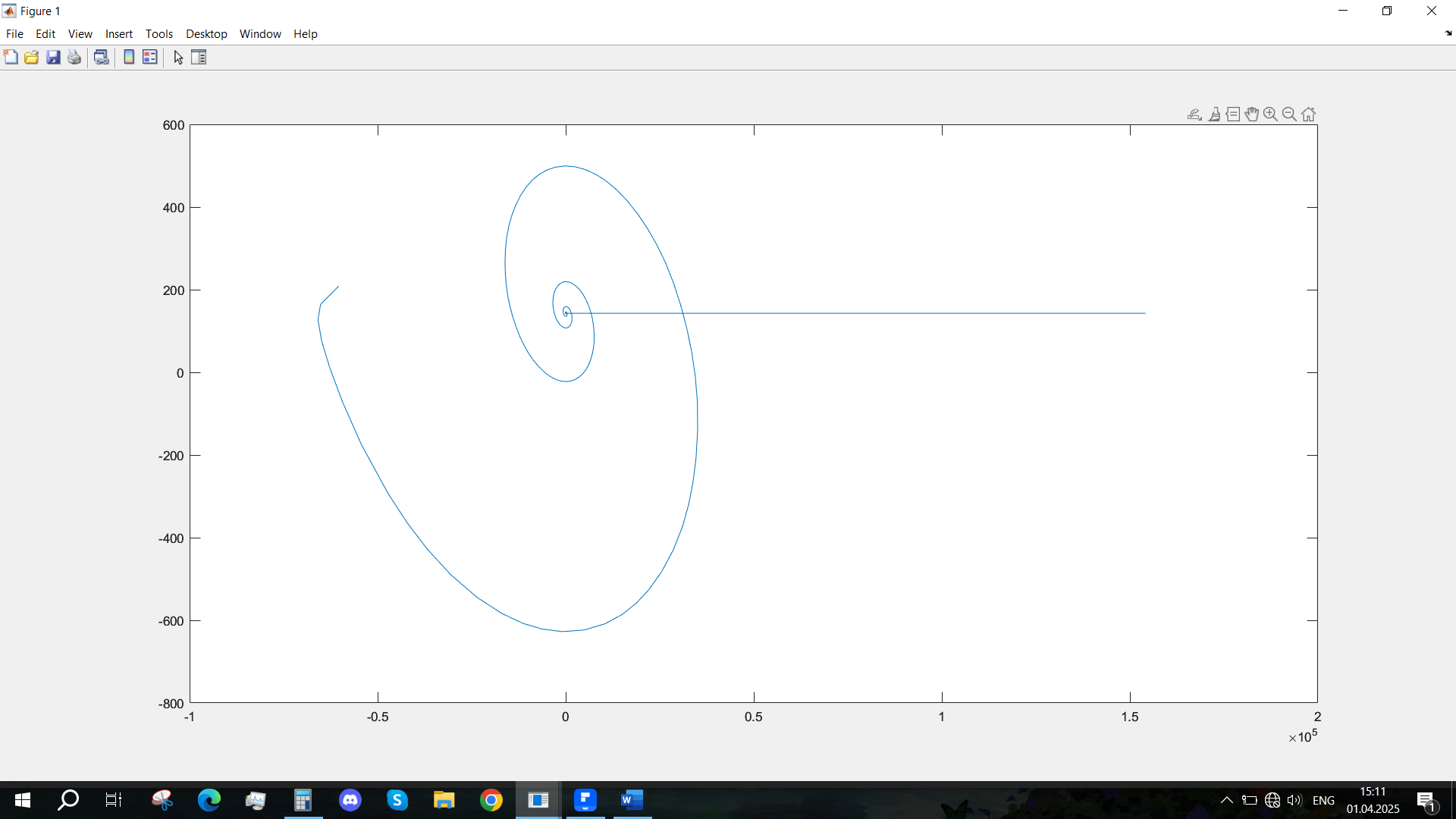
Рис. 30 - Фазовый портрет Ucn

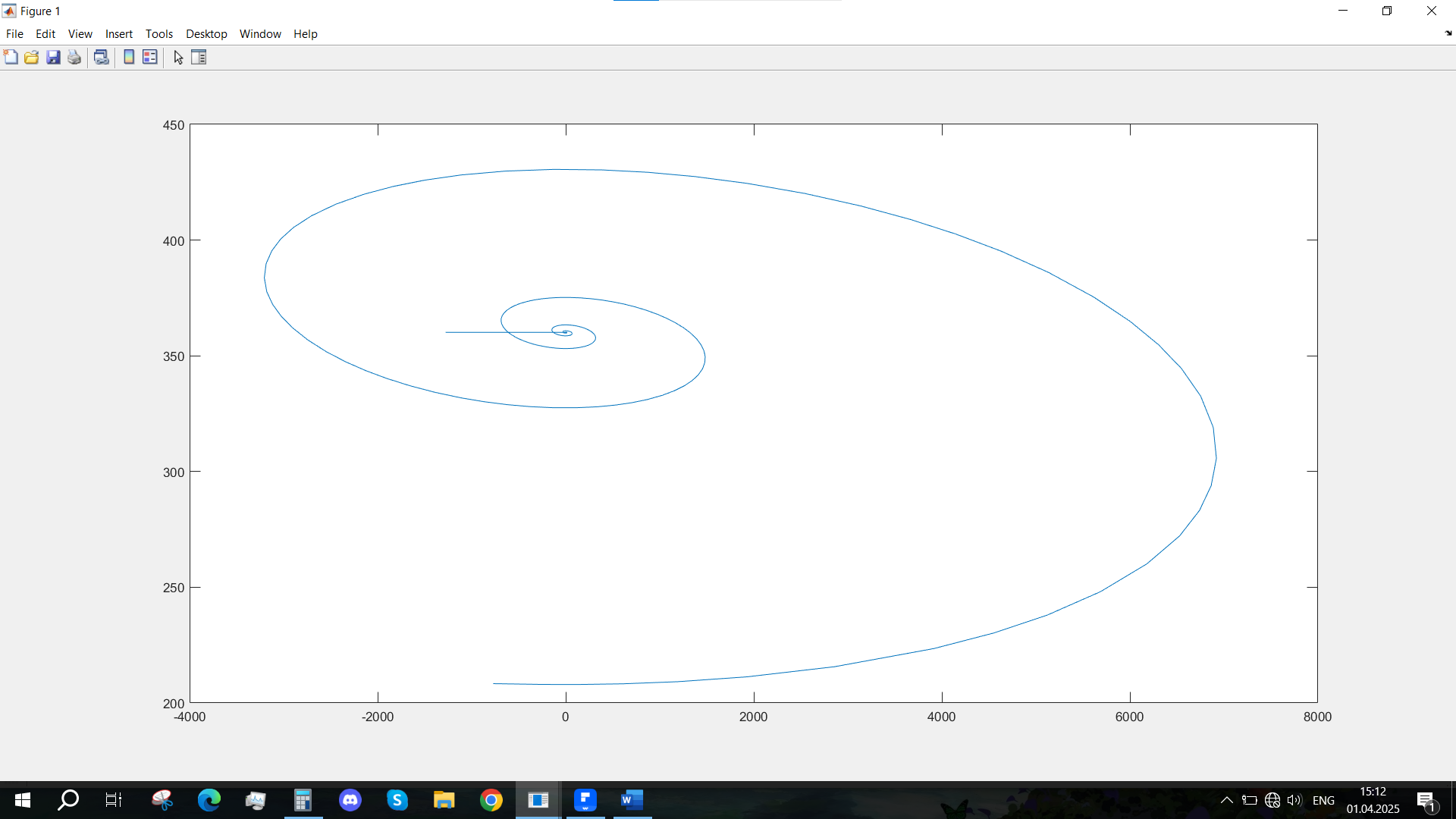
Рис. 31 - Фазовый портрет Mvn

Mvn меняем на 40%

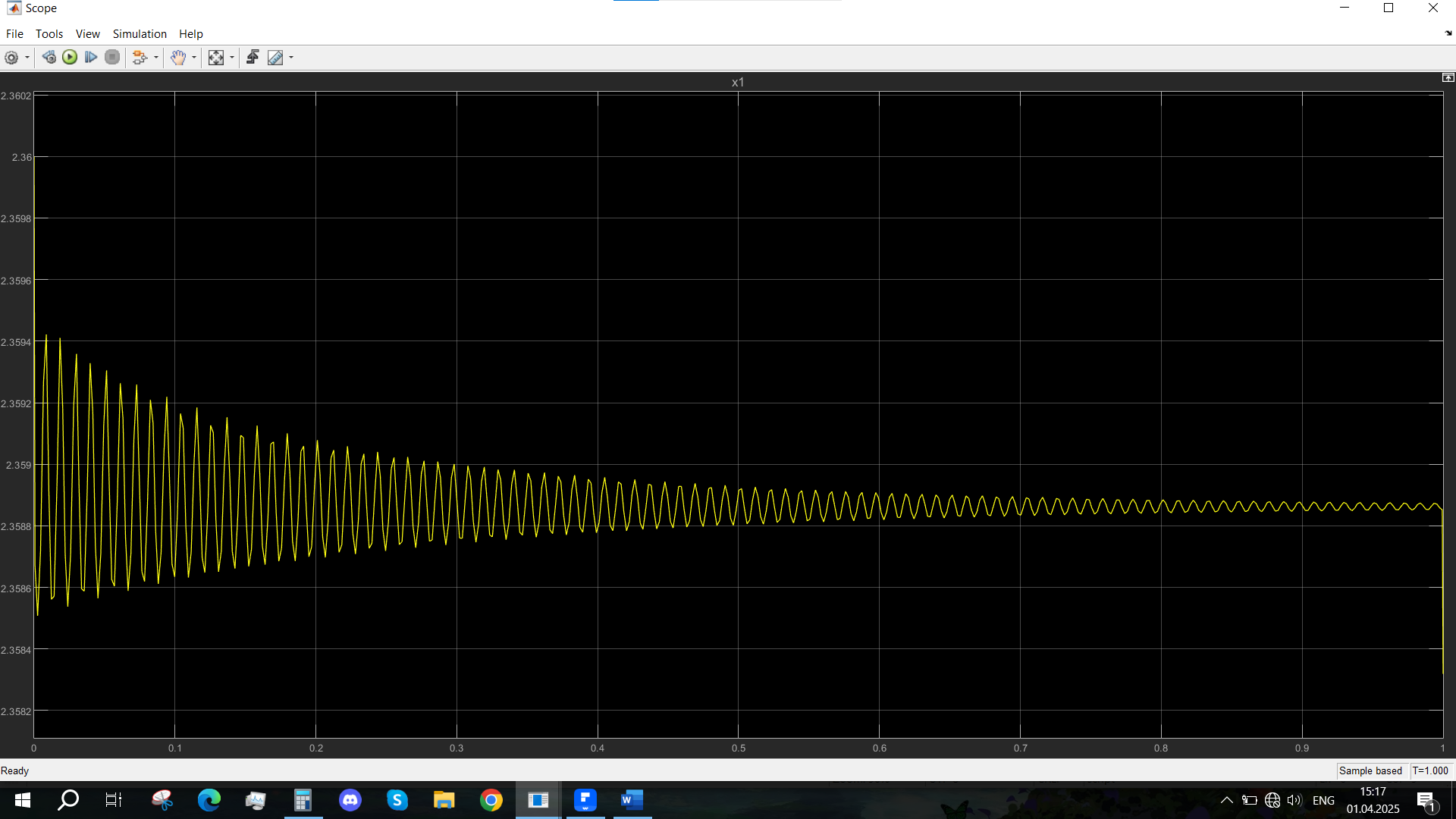
Рис. 32 - Переходная характеристика Uvn

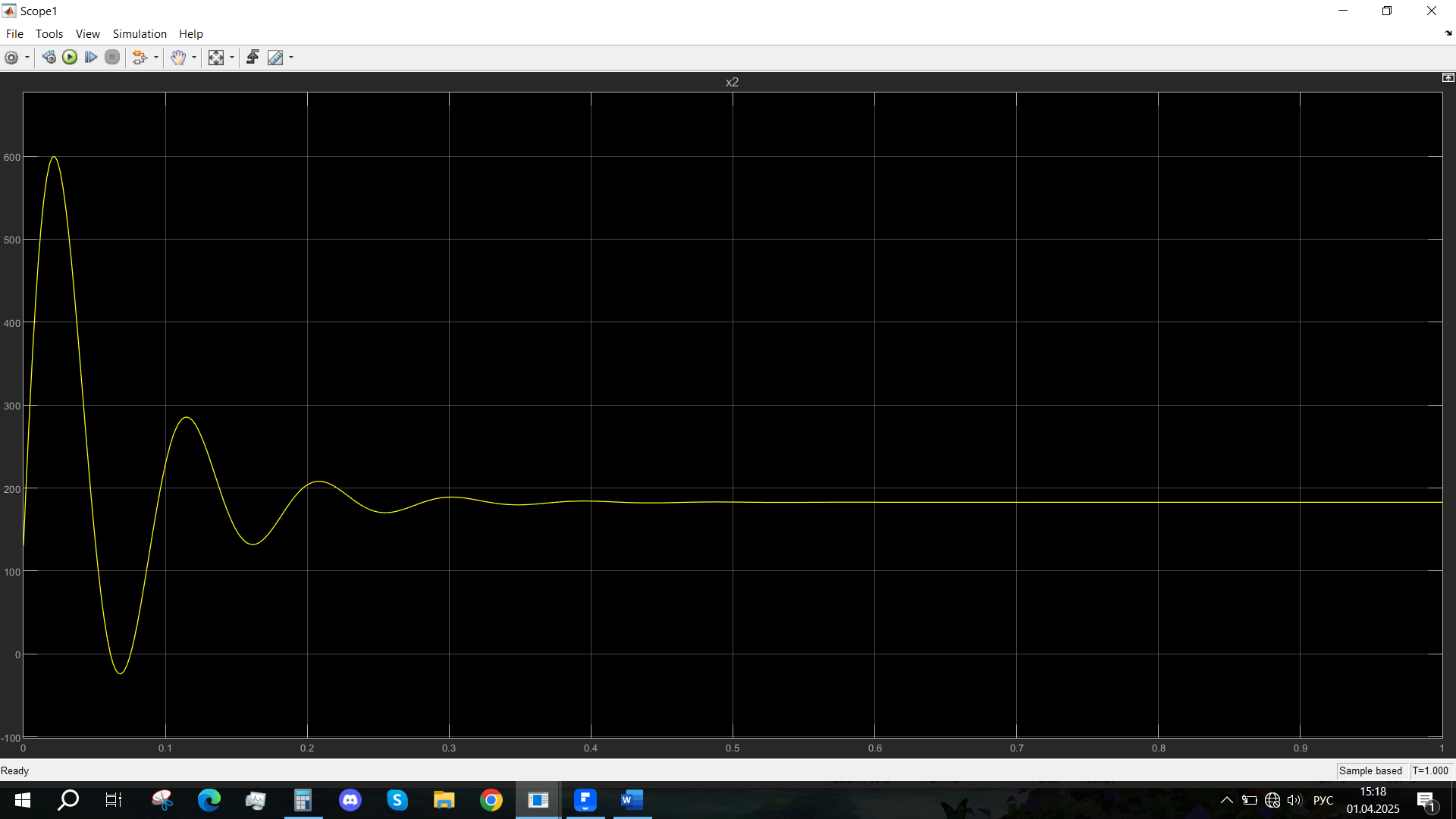
Рис. 33 - Переходная характеристика Ucn

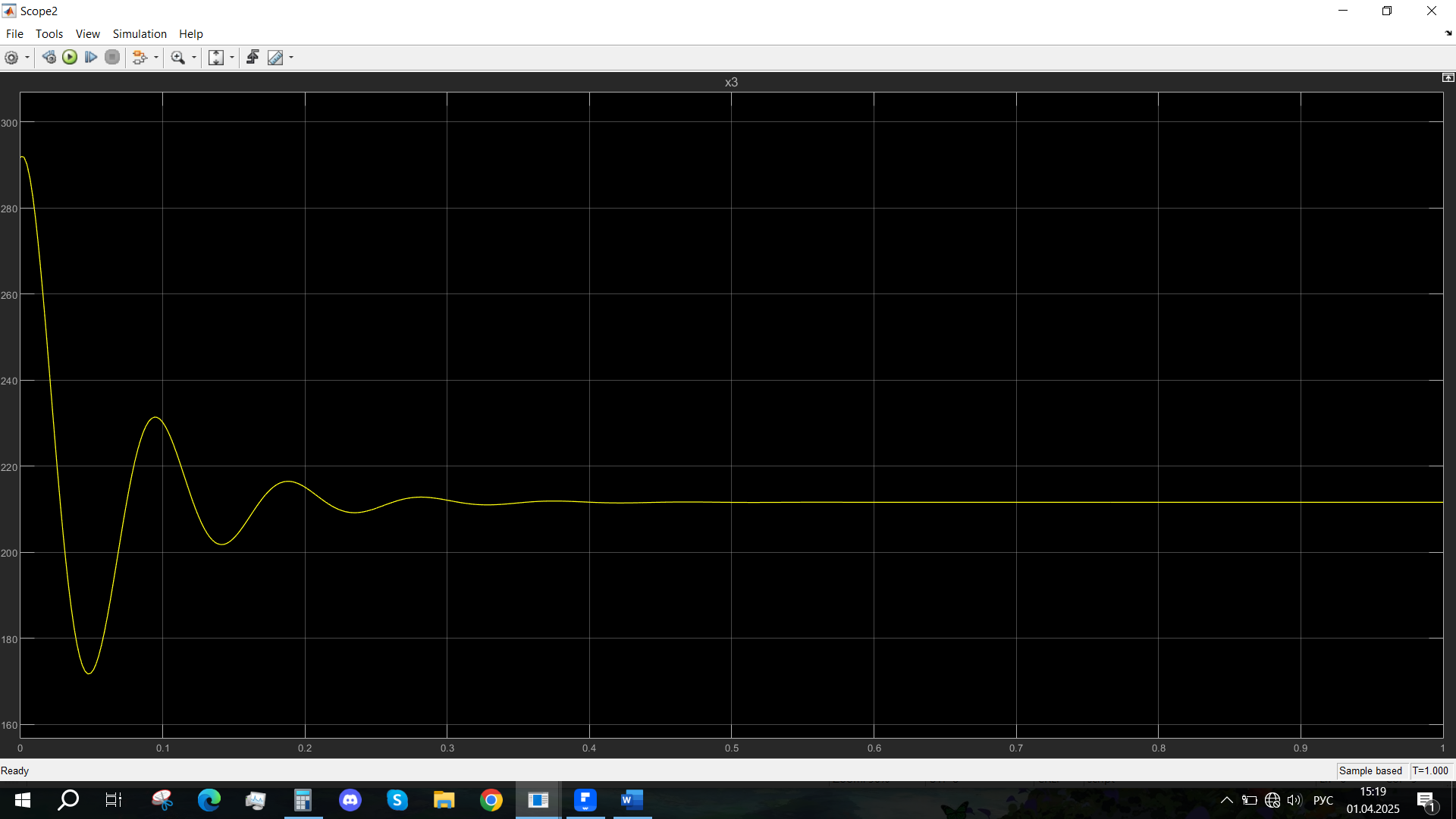
Рис. 34 - Переходная характеристика Mvn

Рис. 35 - Фазовый портрет Uvn

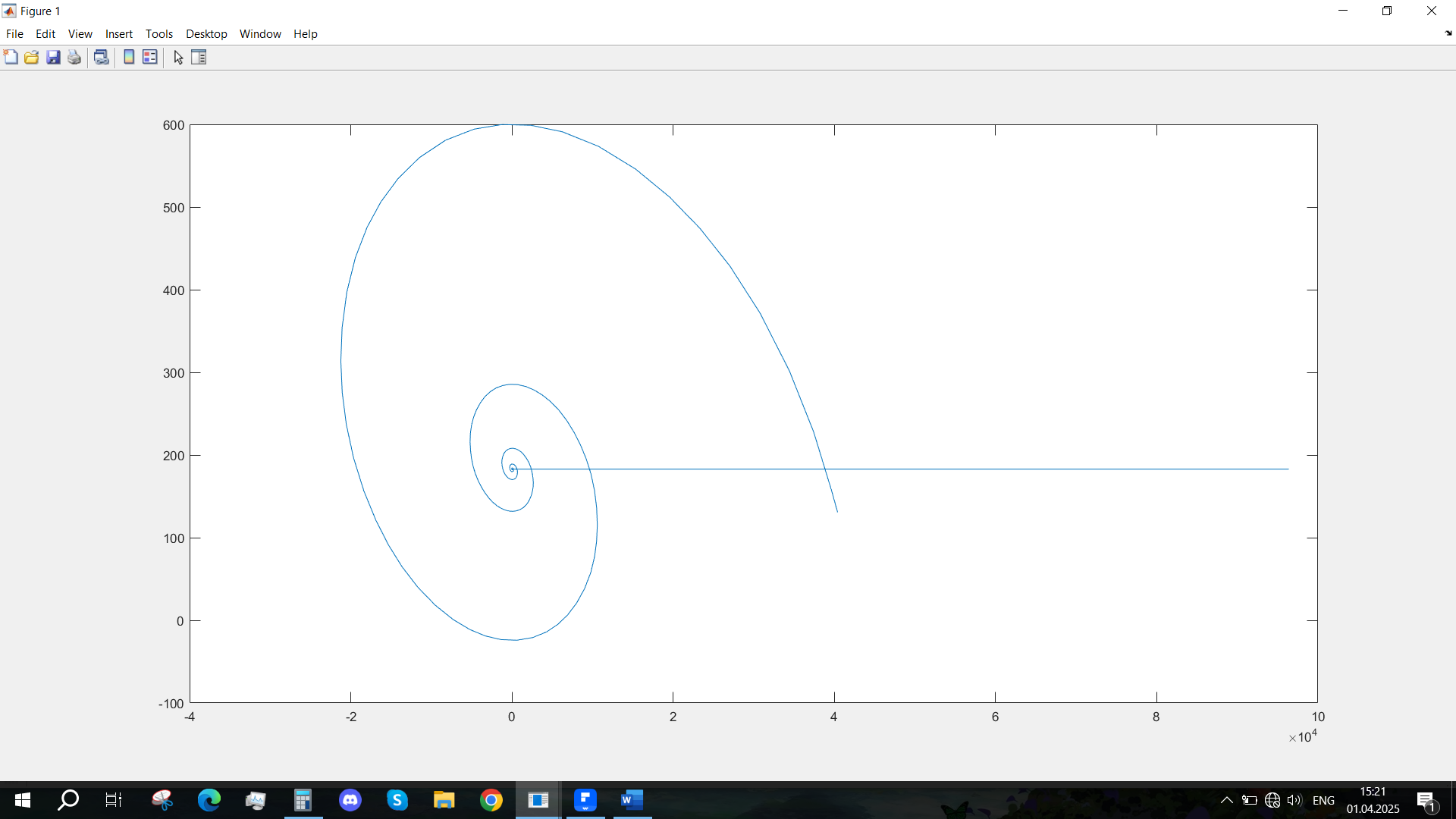
Рис. 36 - Фазовый портрет Ucn

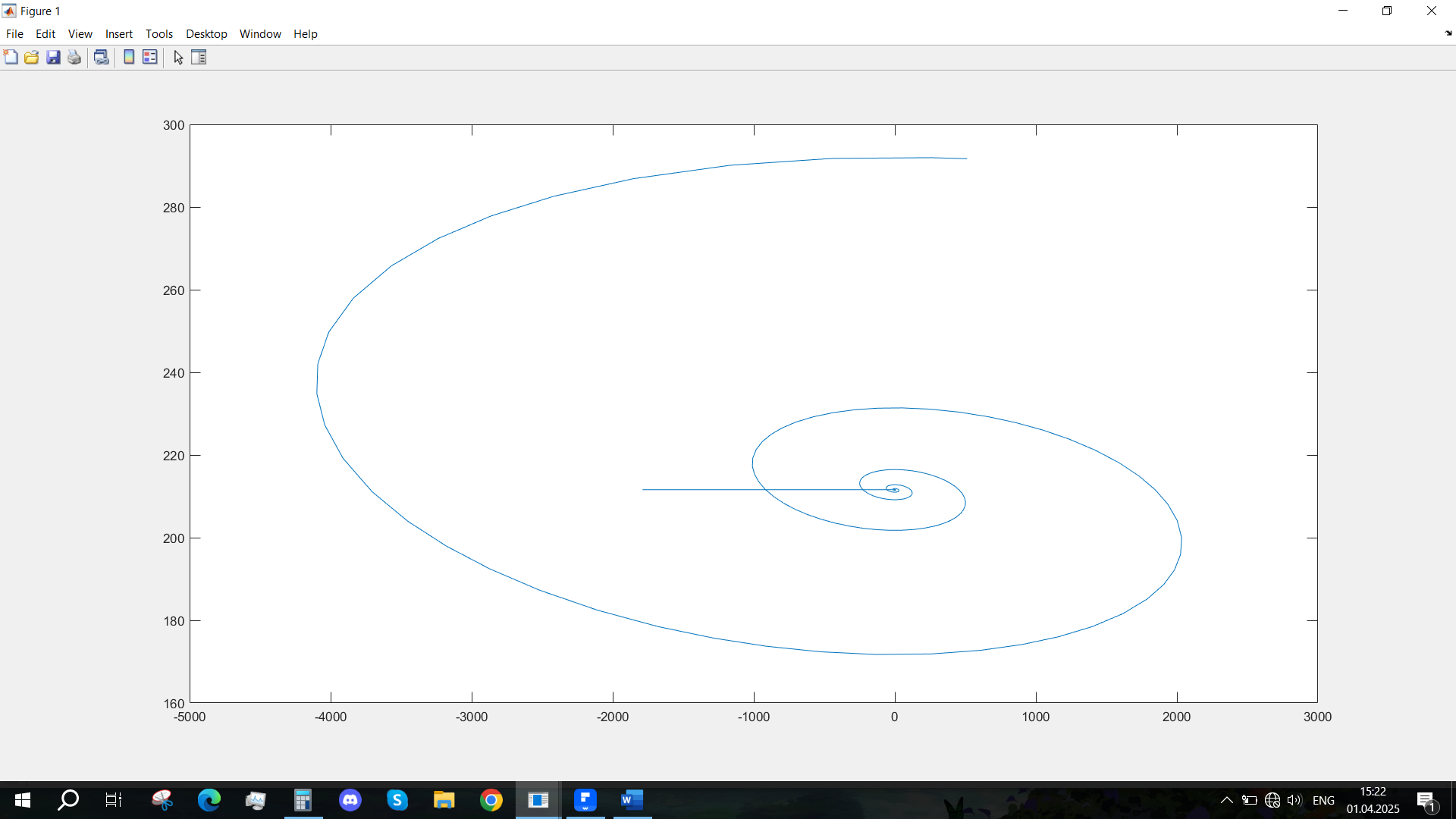
Рис. 37 - Фазовый портрет Mvn

Mvn меняем на 60%

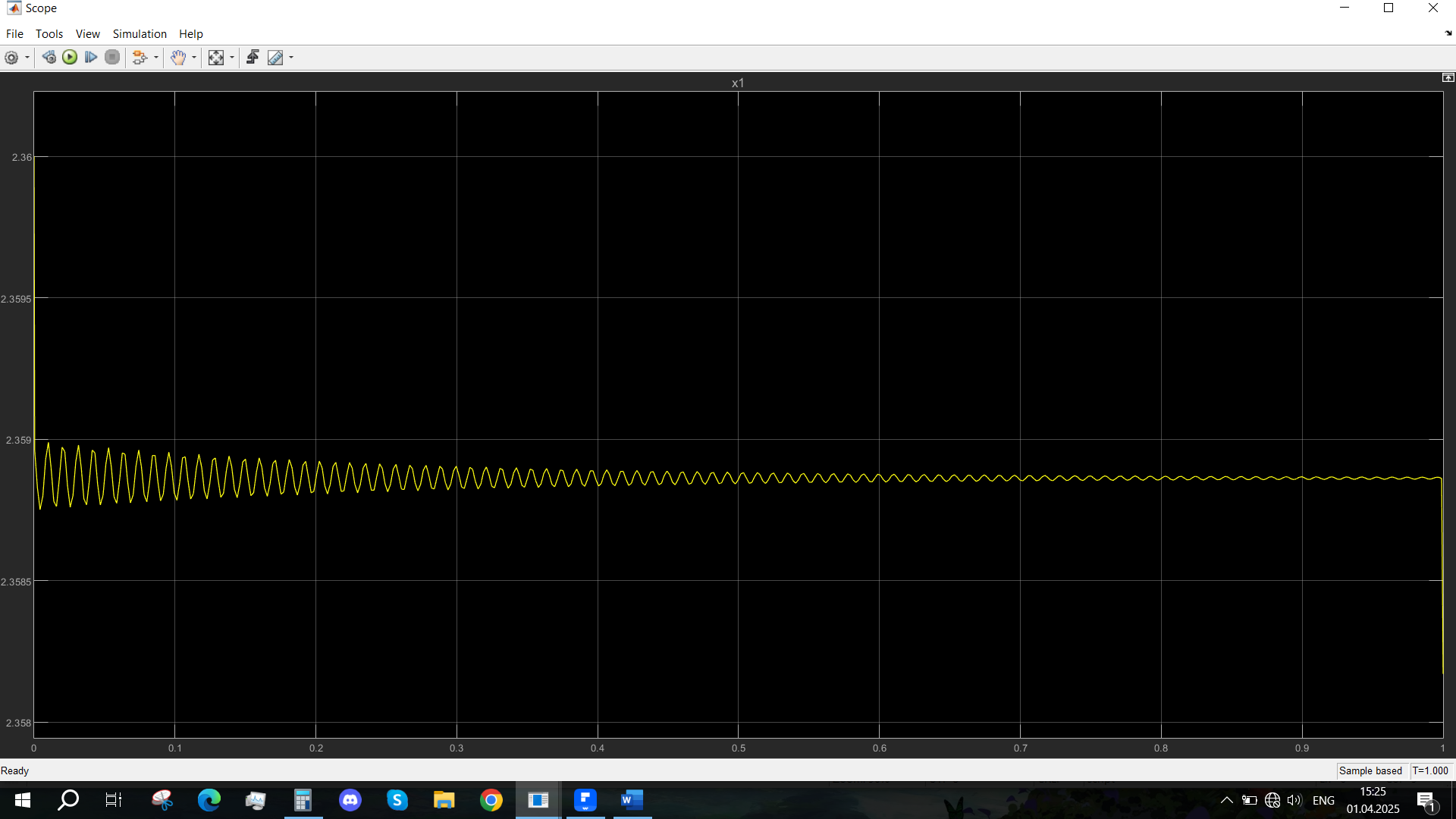
Рис. 38 - Переходная характеристика Uvn

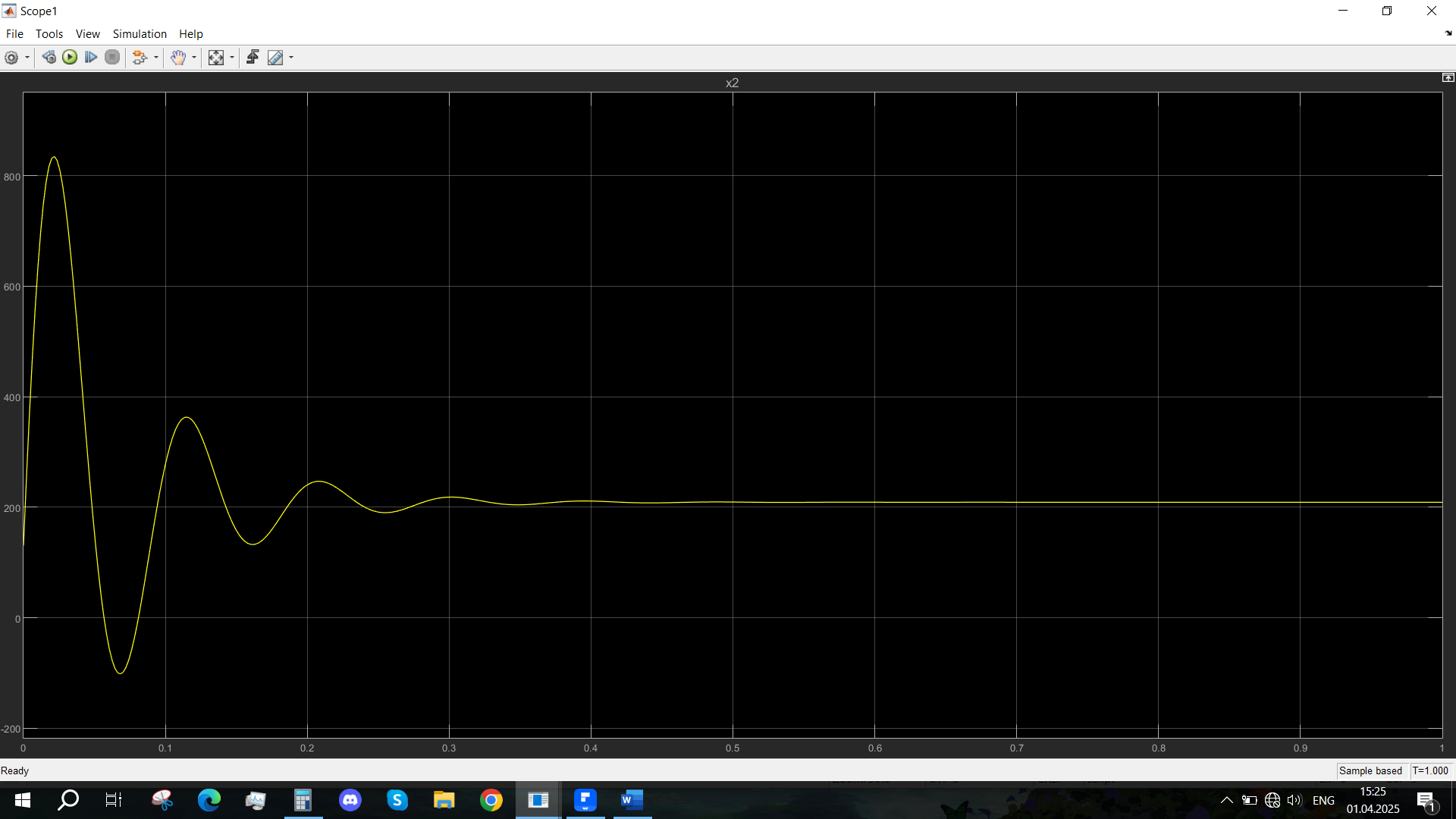
Рис. 39 - Переходная характеристика Ucn

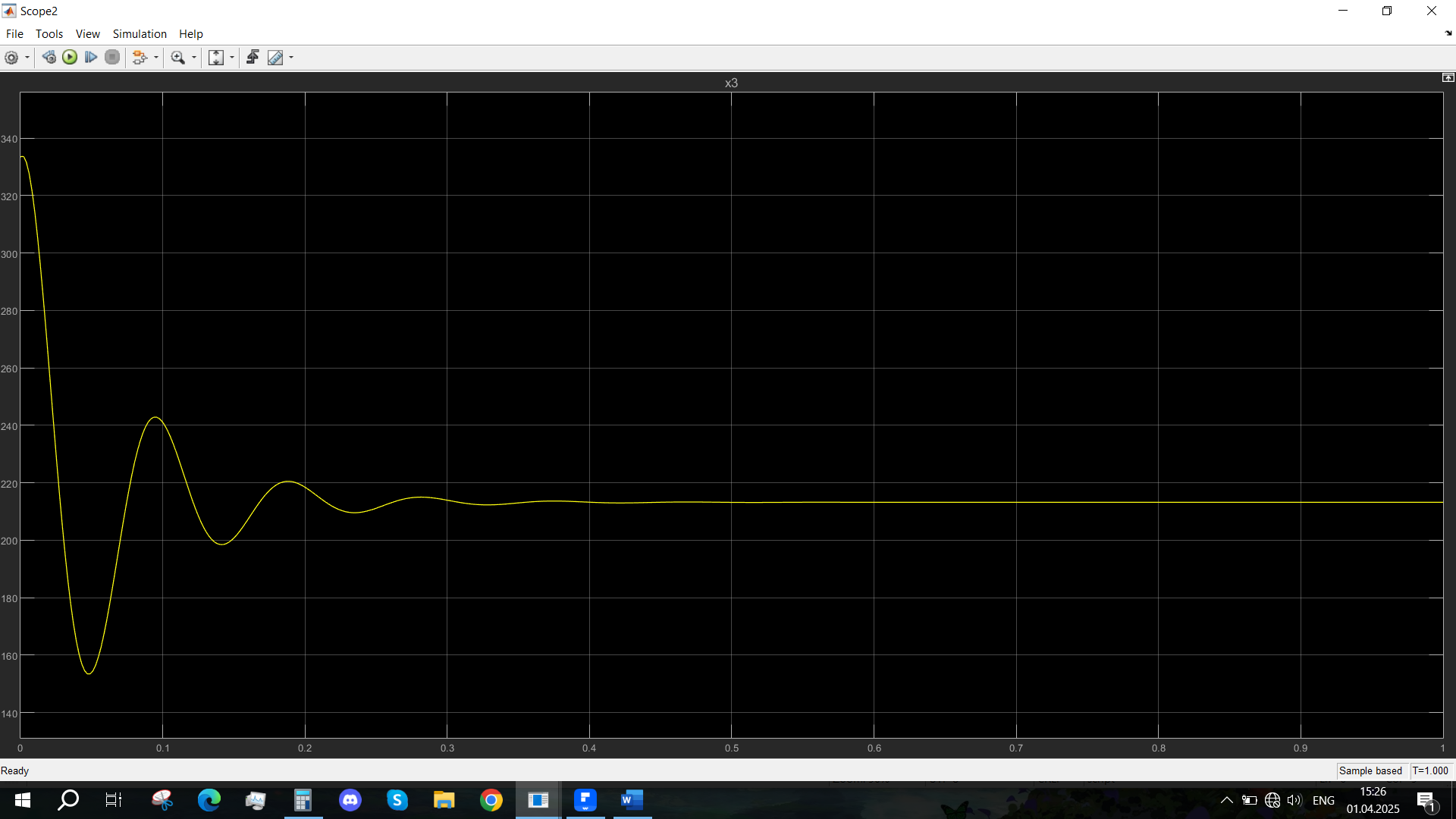
Рис. 40 - Переходная характеристика Mvn

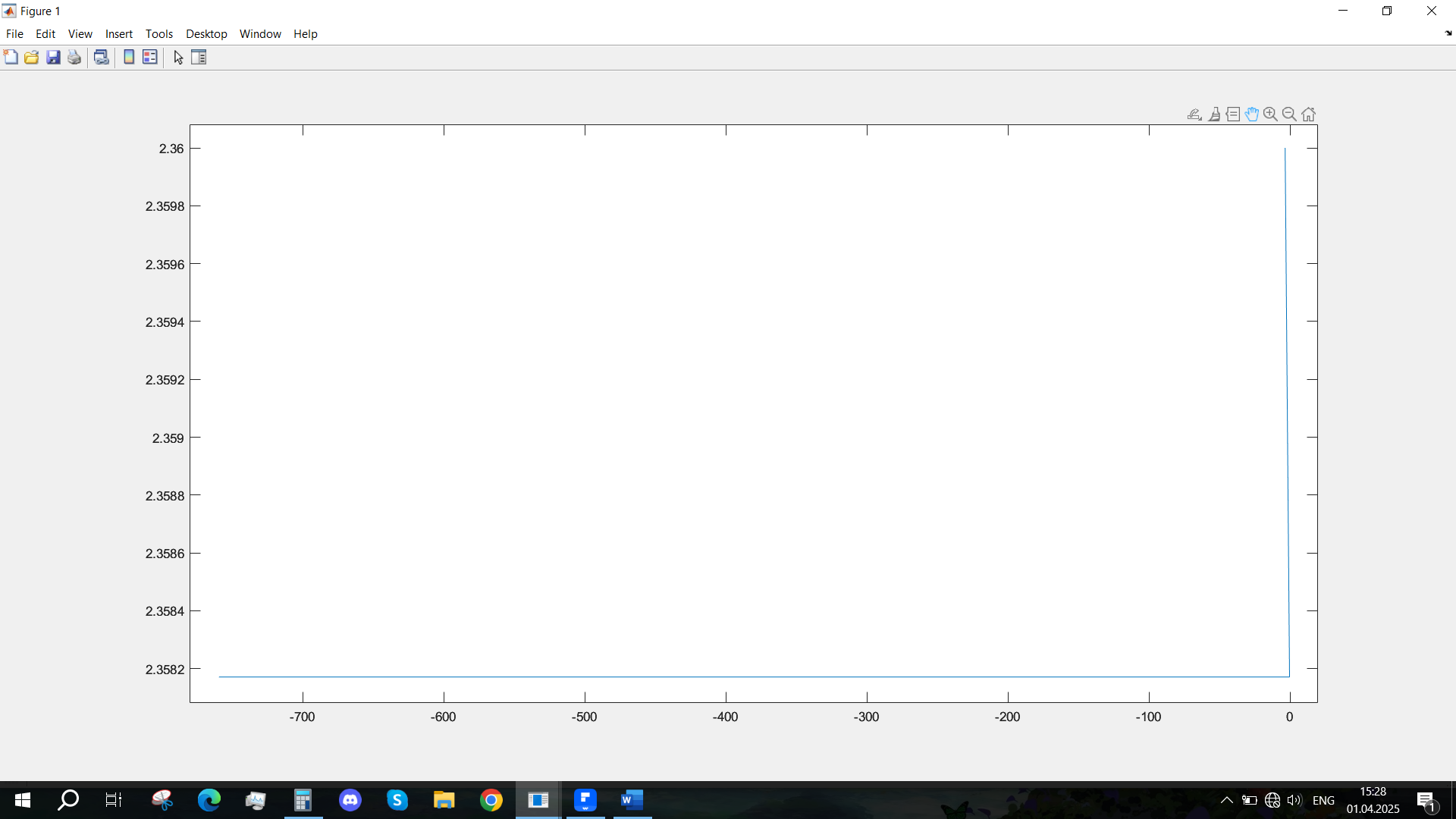
Рис. 41 - Фазовый портрет Uvn

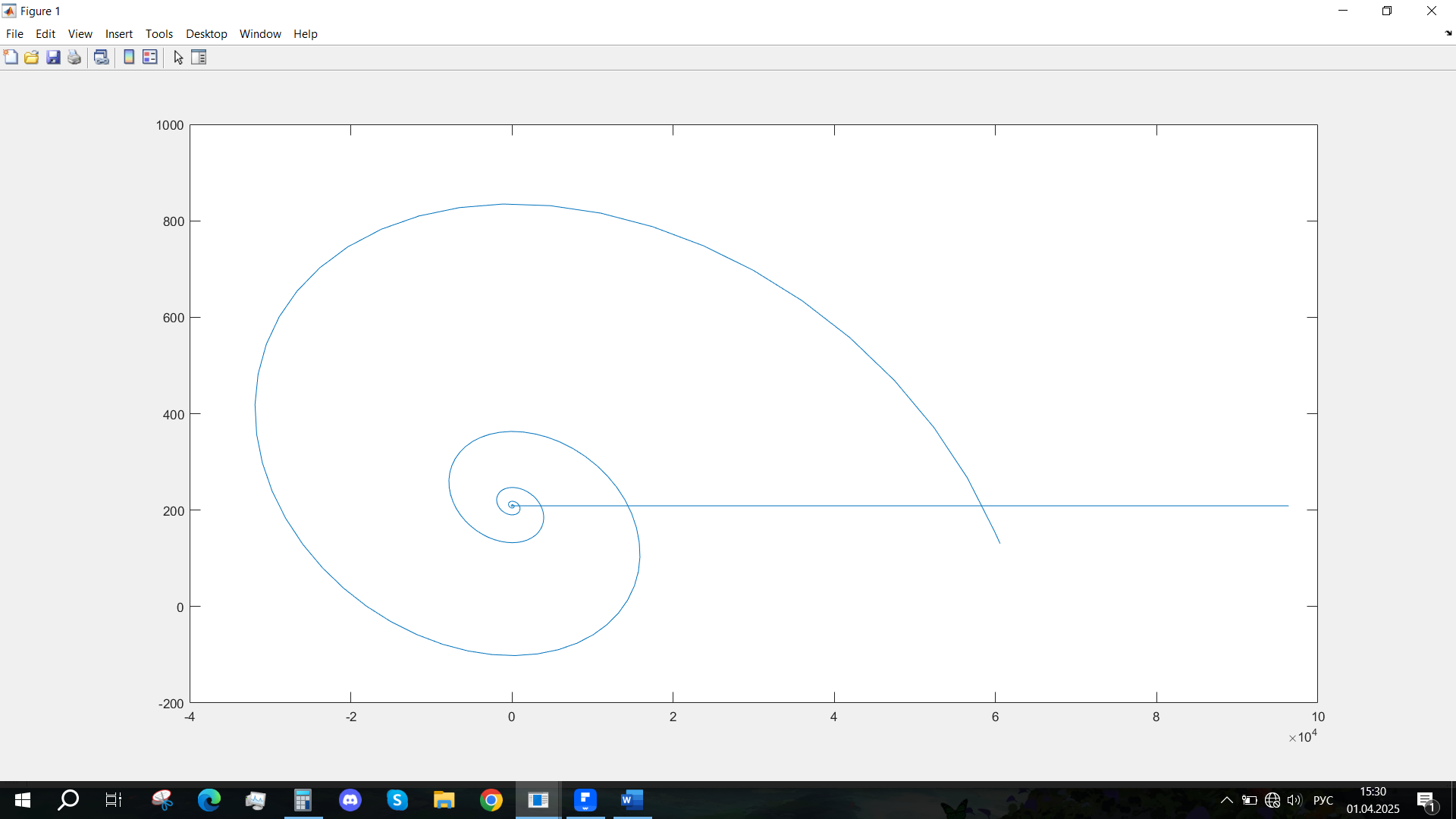
Рис. 42 - Фазовый портрет Ucn

Рис. 43 - Фазовый портрет Mvn

Меняем Uvn и Ucn на 40%

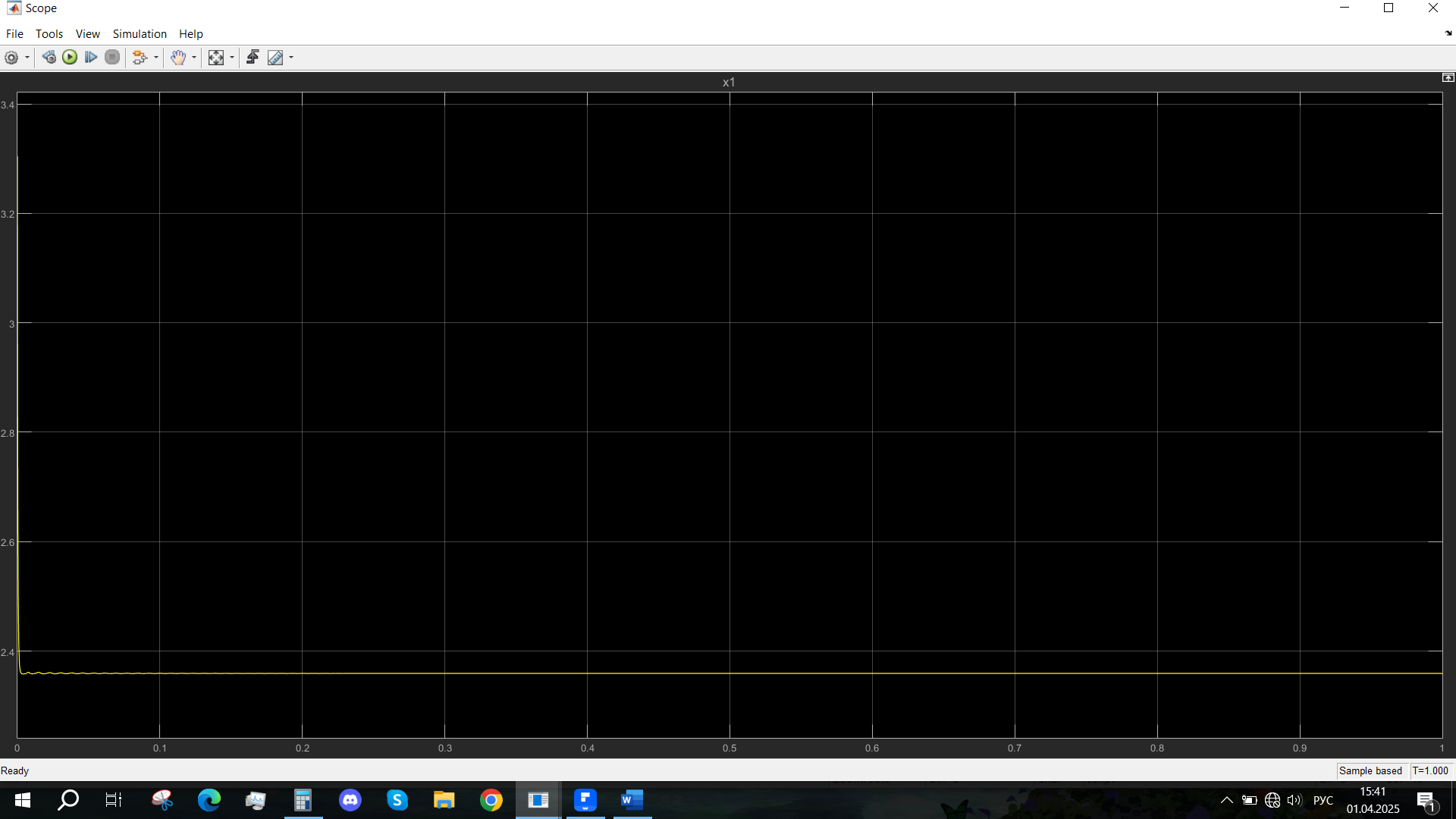
Рис. 44 - Переходная характеристика Uvn

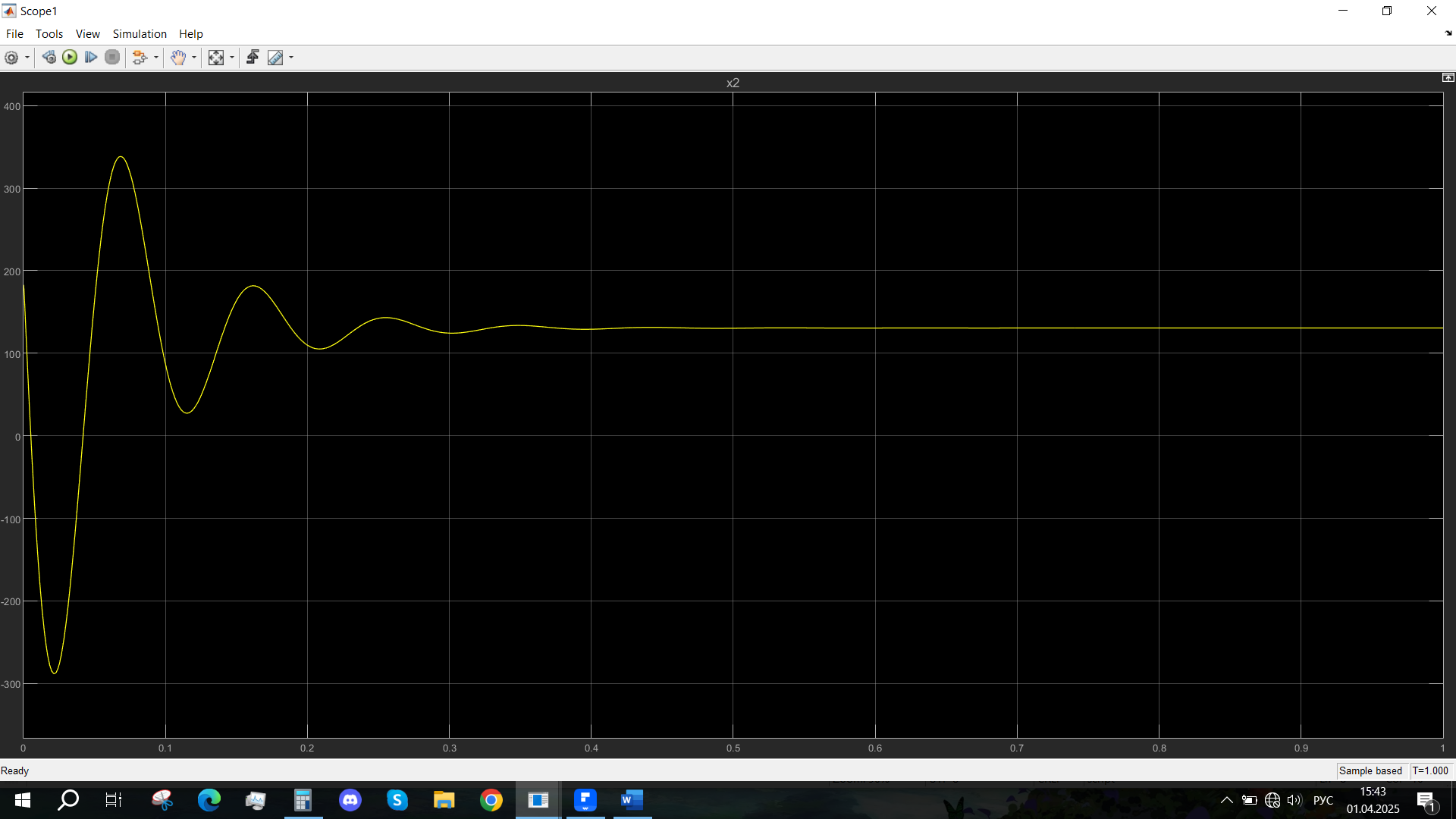
Рис. 45 - Переходная характеристика Ucn

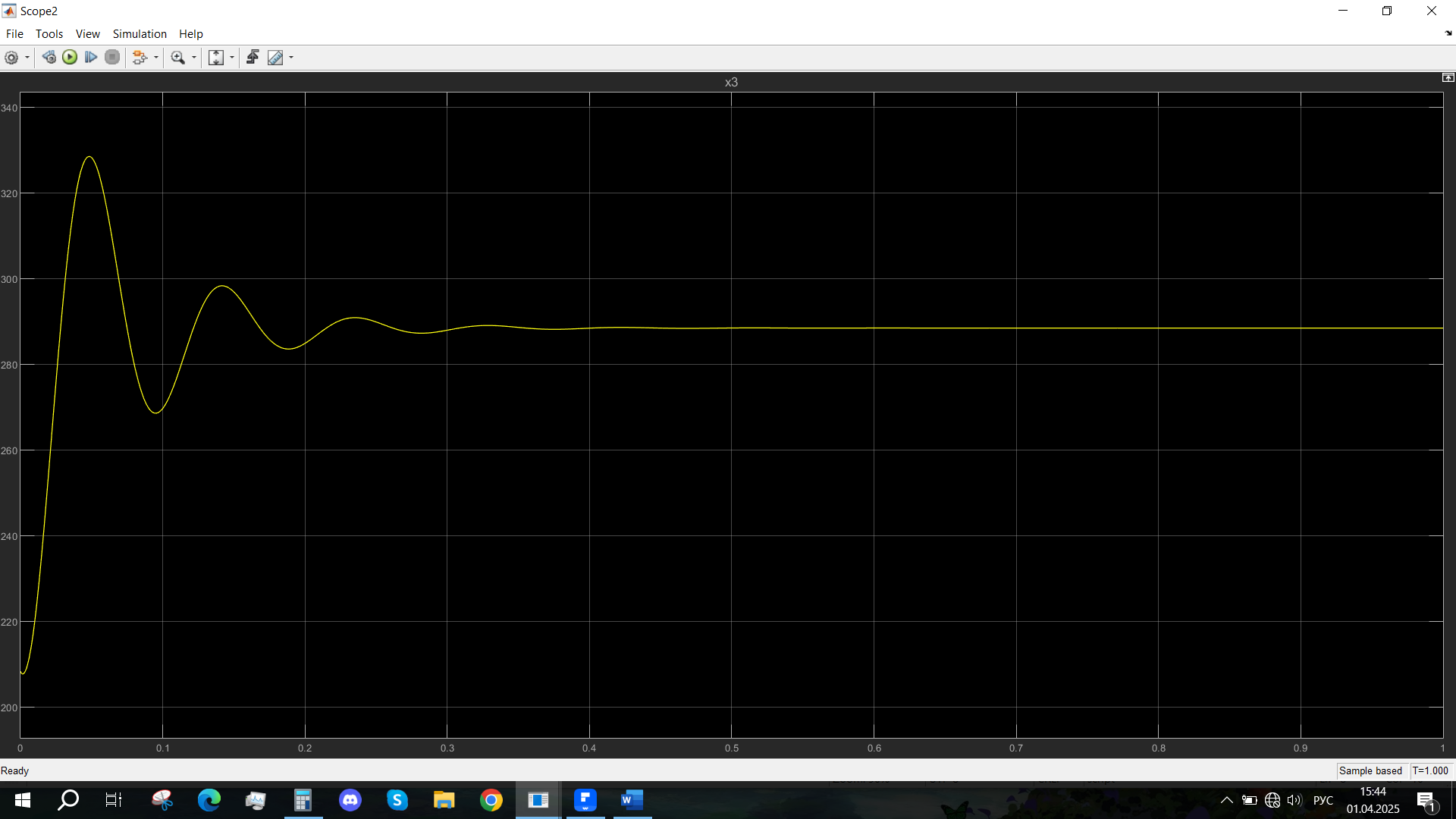
Рис. 46 - Переходная характеристика Mvn

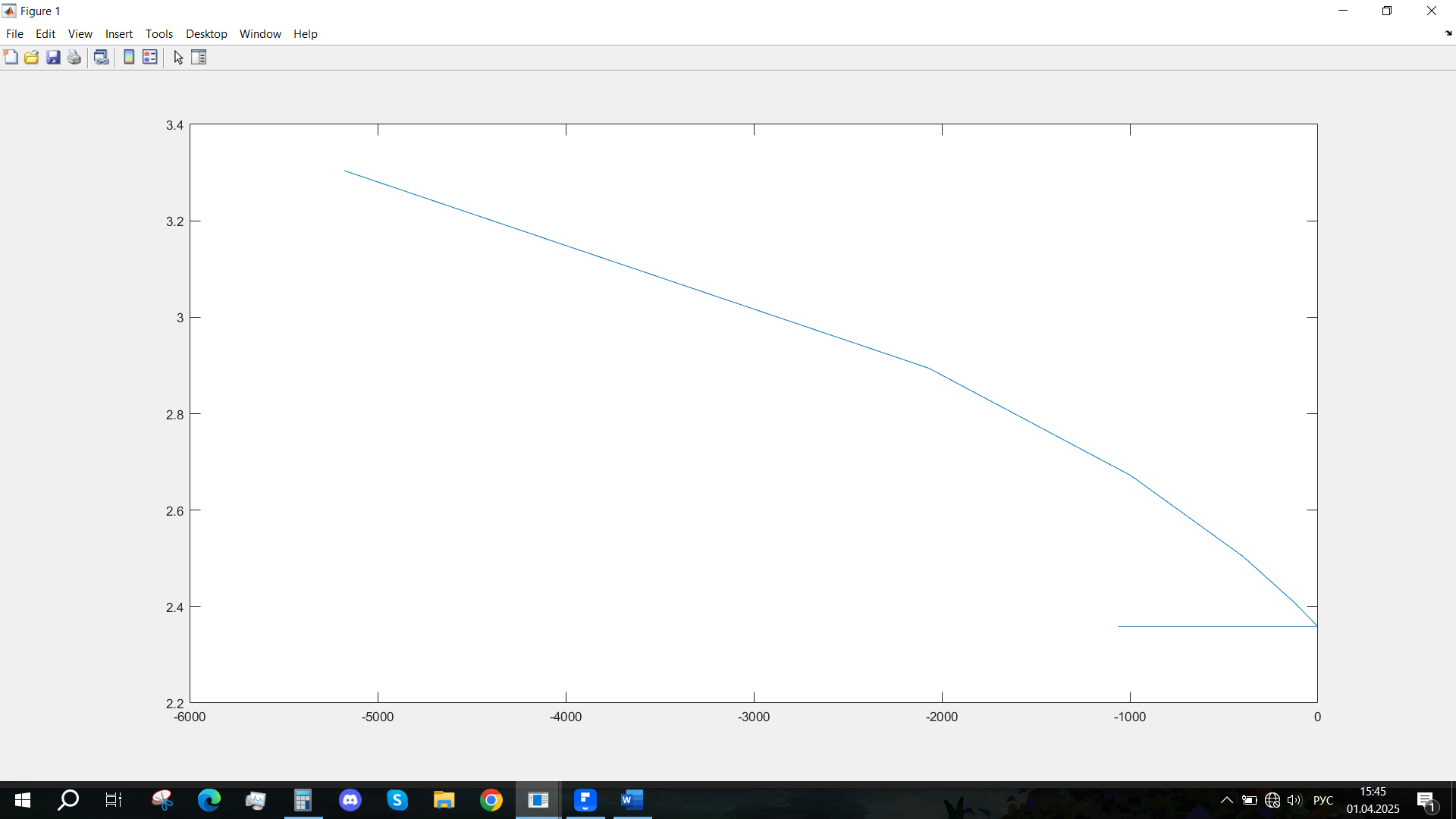
Рис. 47 - Фазовый портрет Uvn

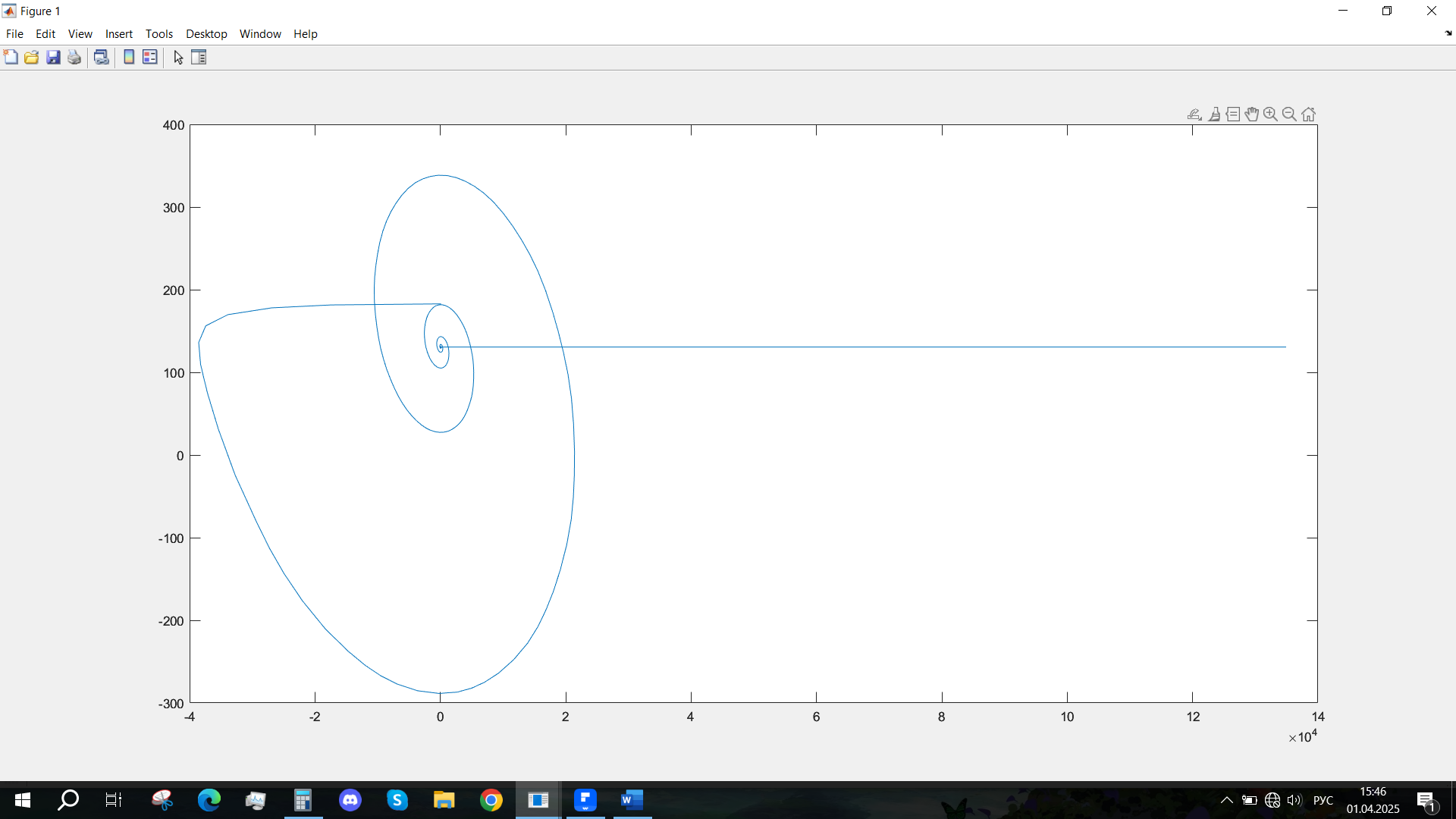
Рис. 48 - Фазовый портрет Ucn

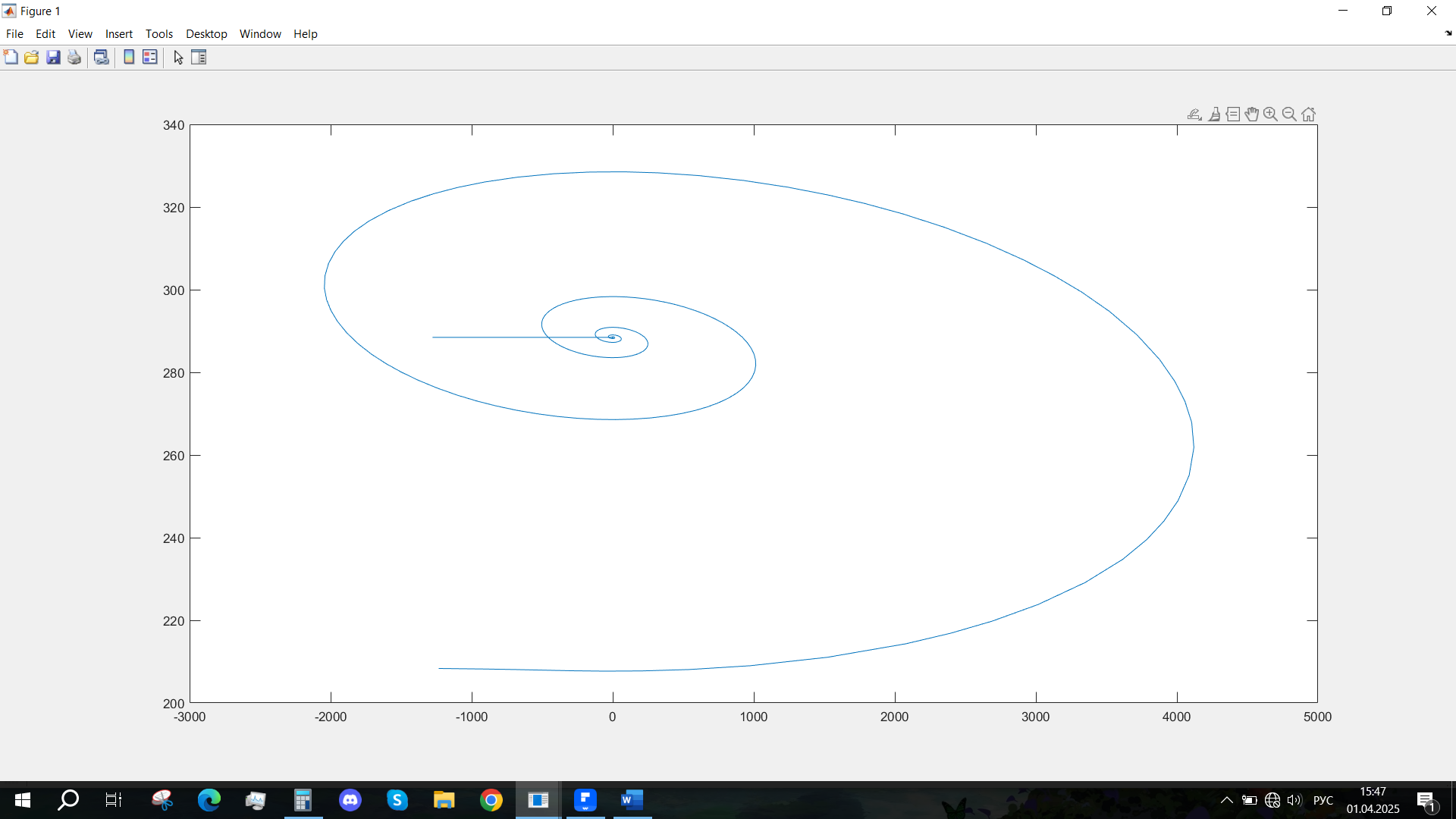
Рис. 49 - Фазовый портрет Mvn

Ucn и Mvn на 40%

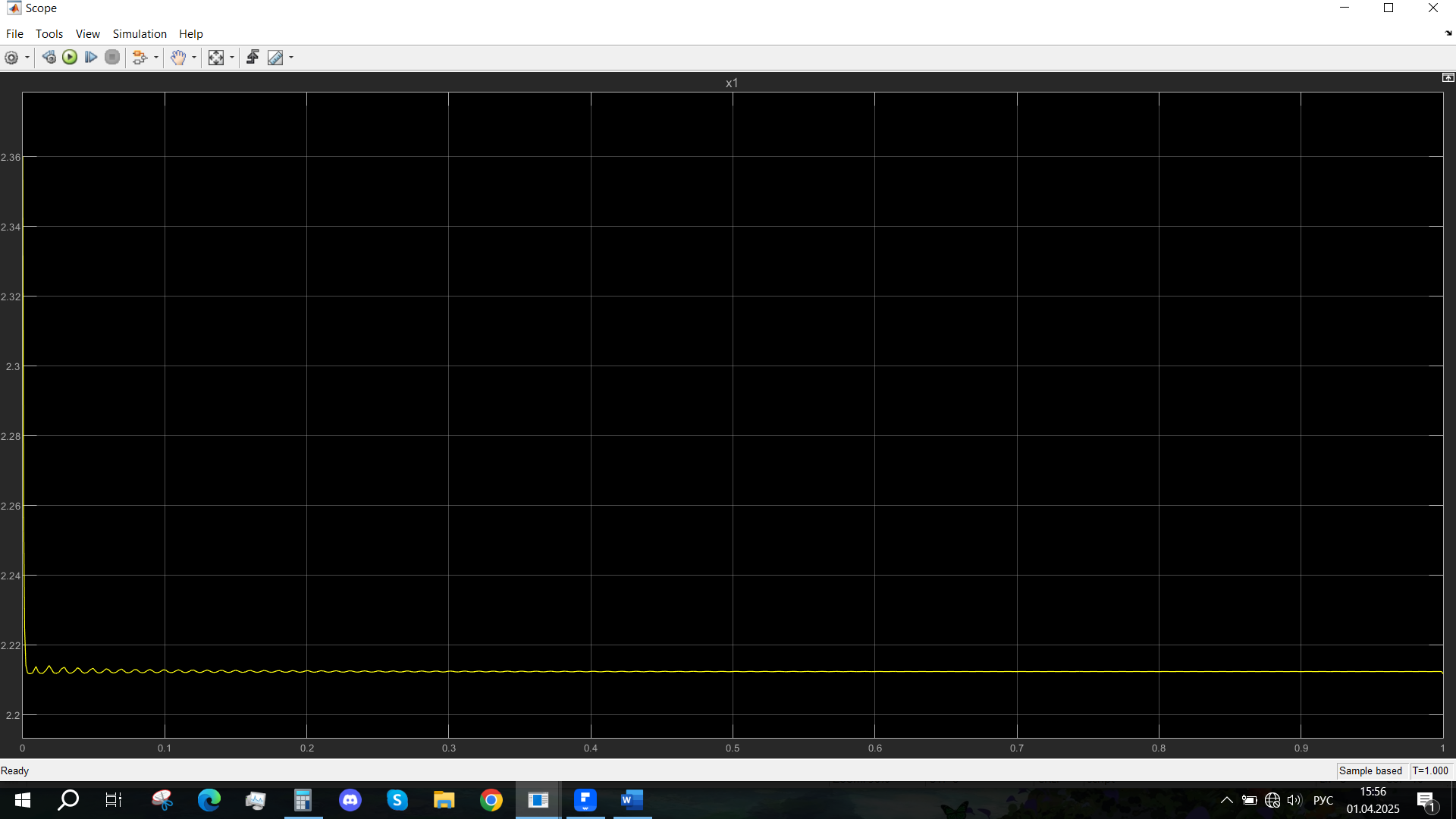
Рис. 50 - Переходная характеристика Uvn

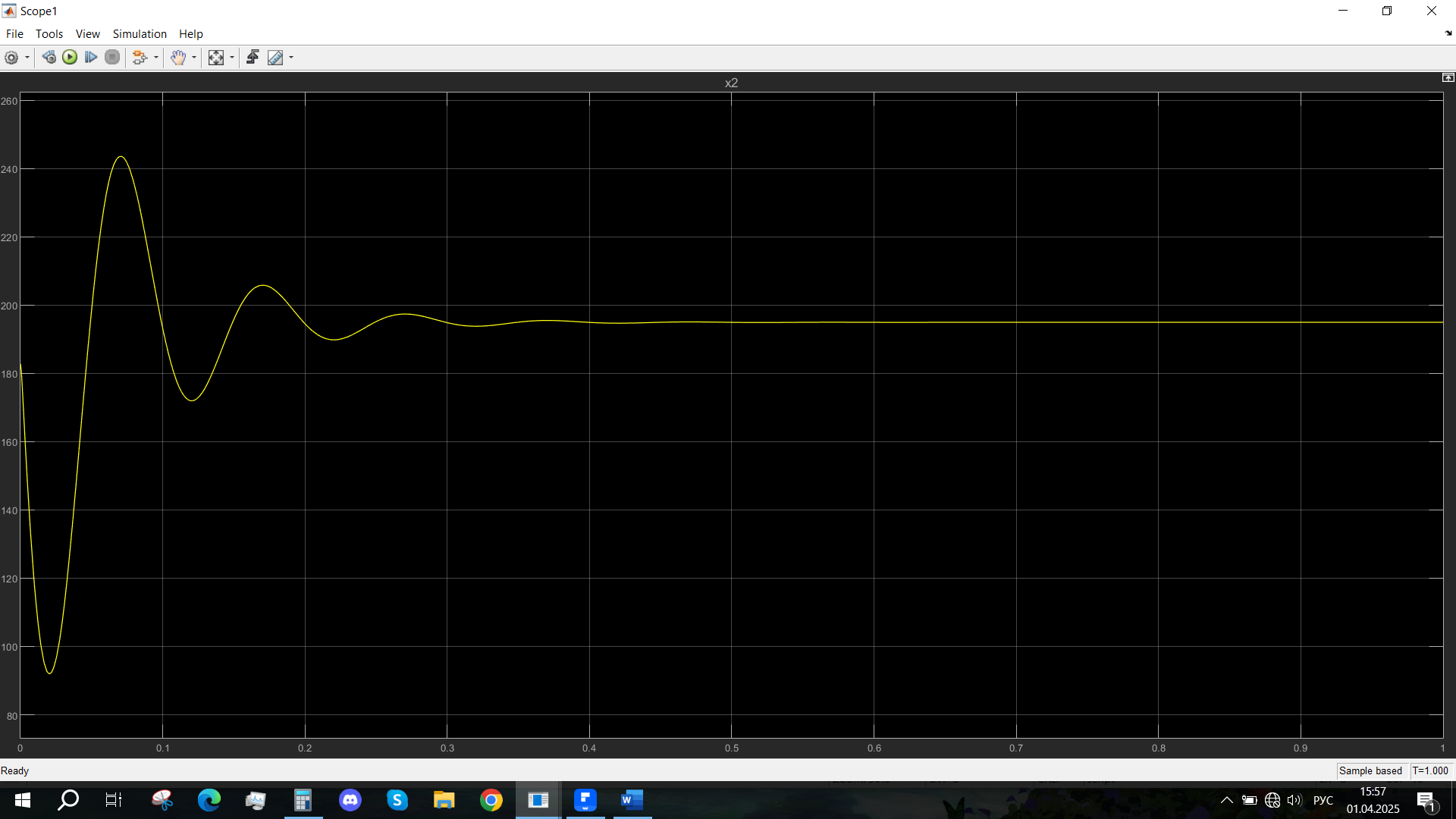
Рис. 51 - Переходная характеристика Ucn

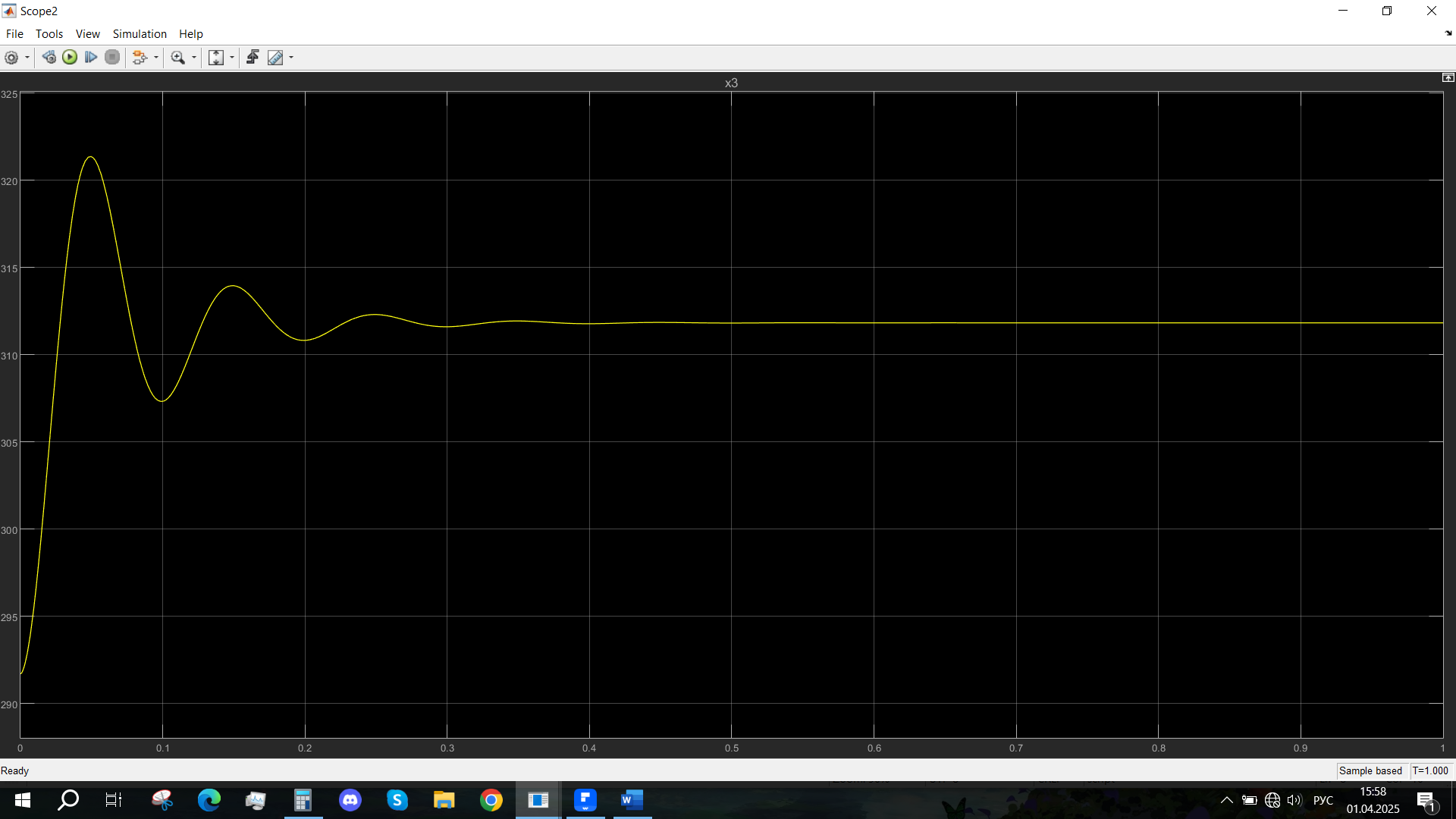
Рис. 52 - Переходная характеристика Mvn

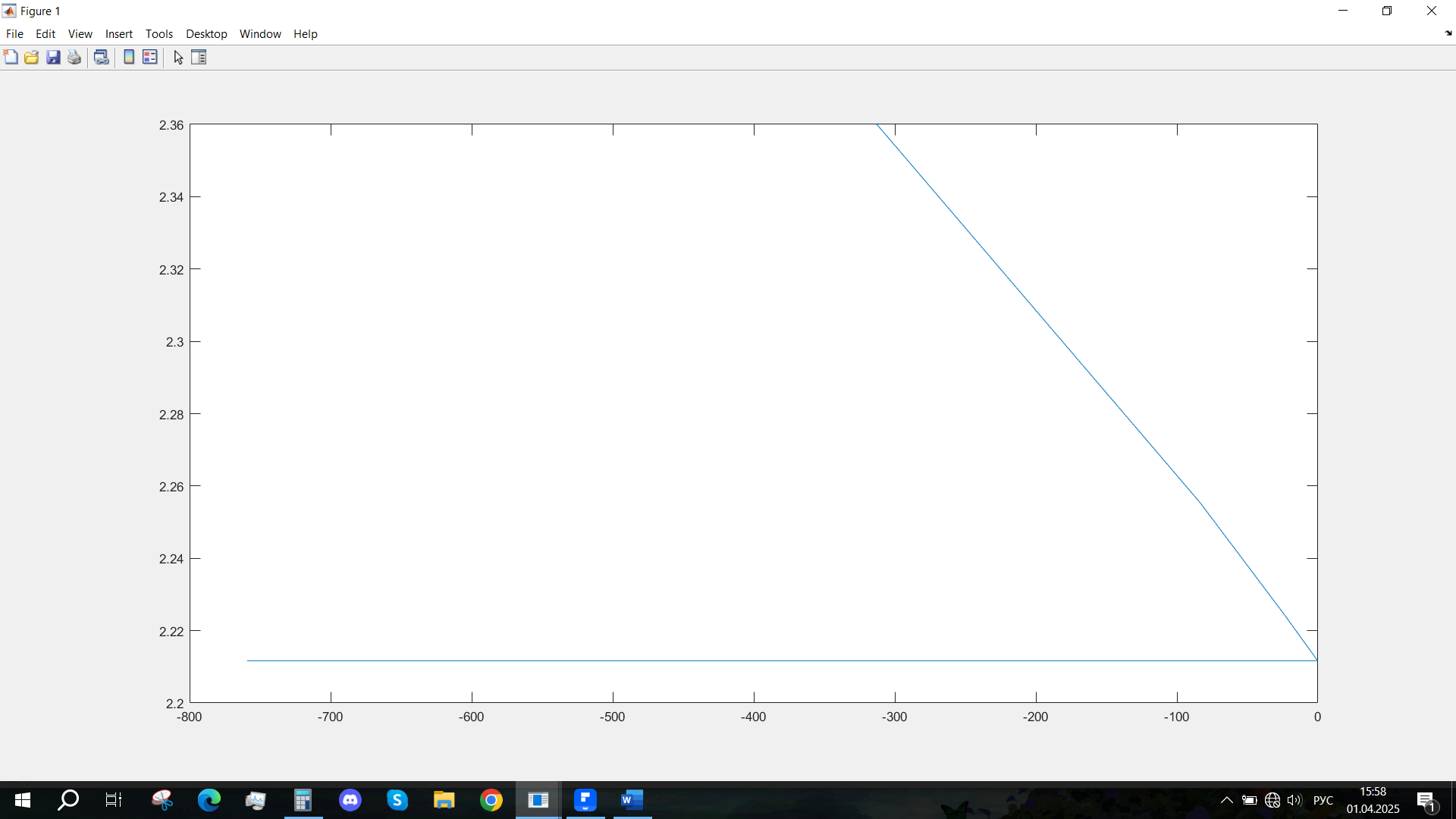
Рис. 53 - Фазовый портрет Uvn

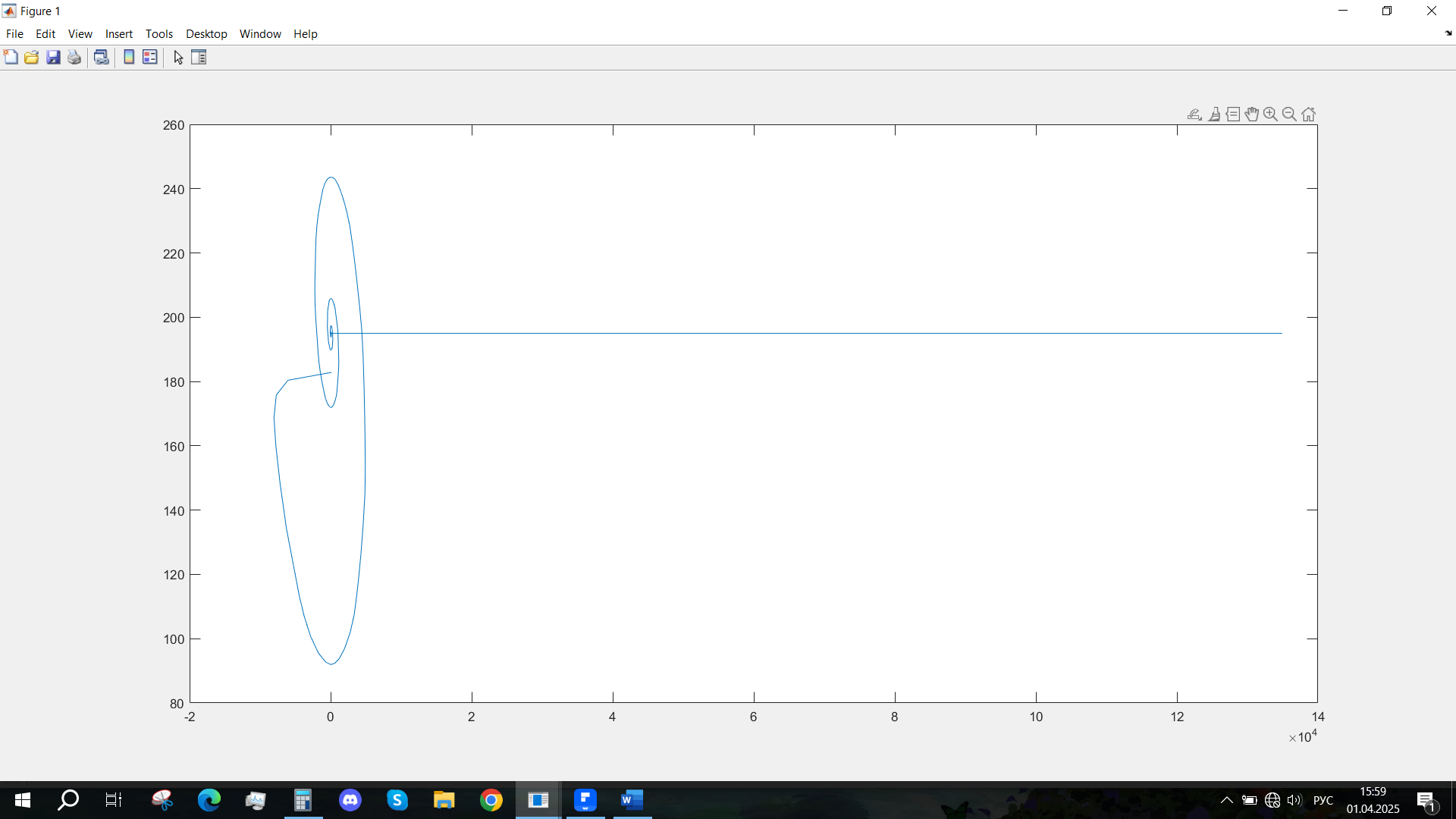
Рис. 54 - Фазовый портрет Ucn

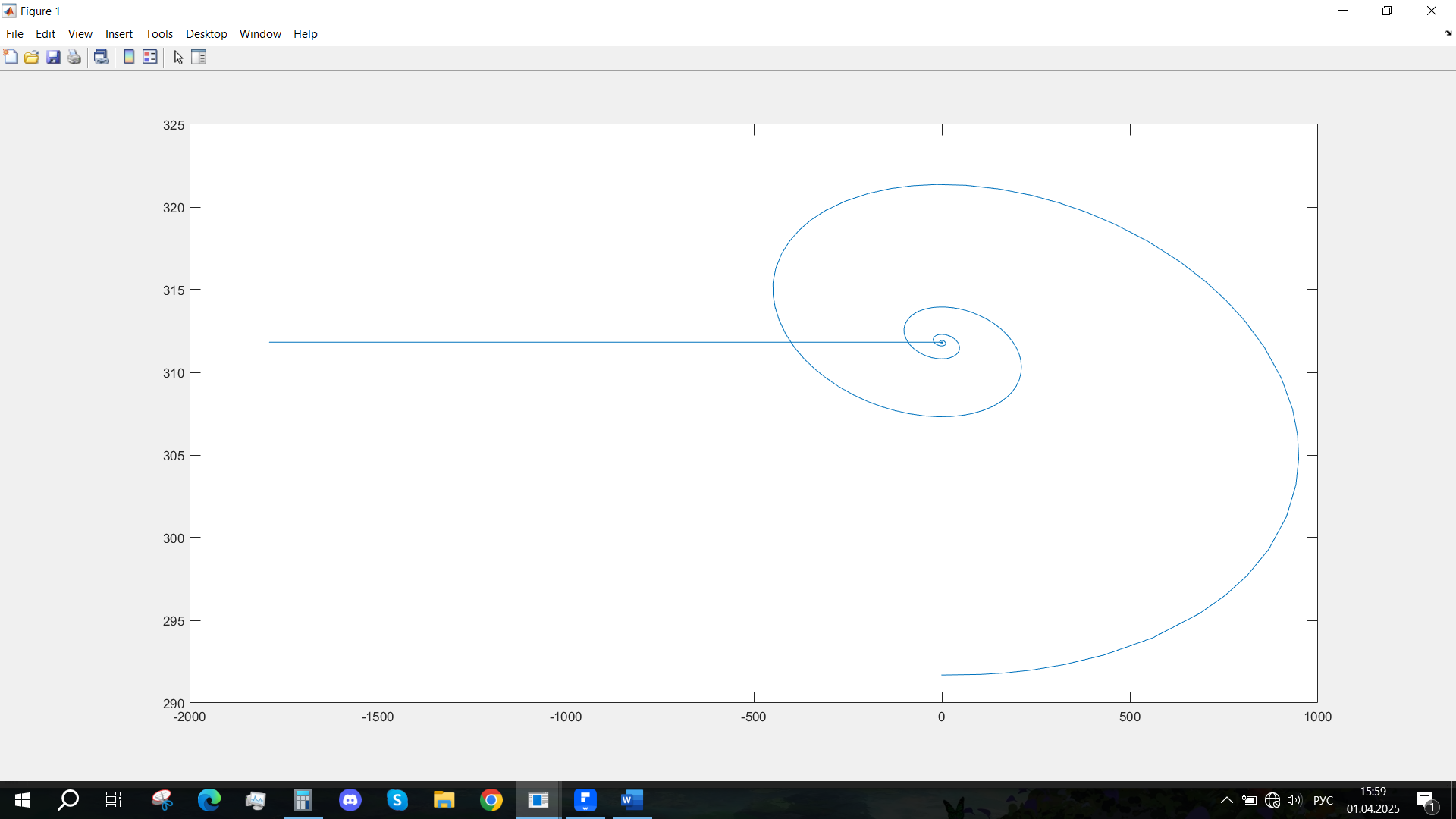
Рис. 55 - Фазовый портрет Mvn

Ucn и Mvn на 60%

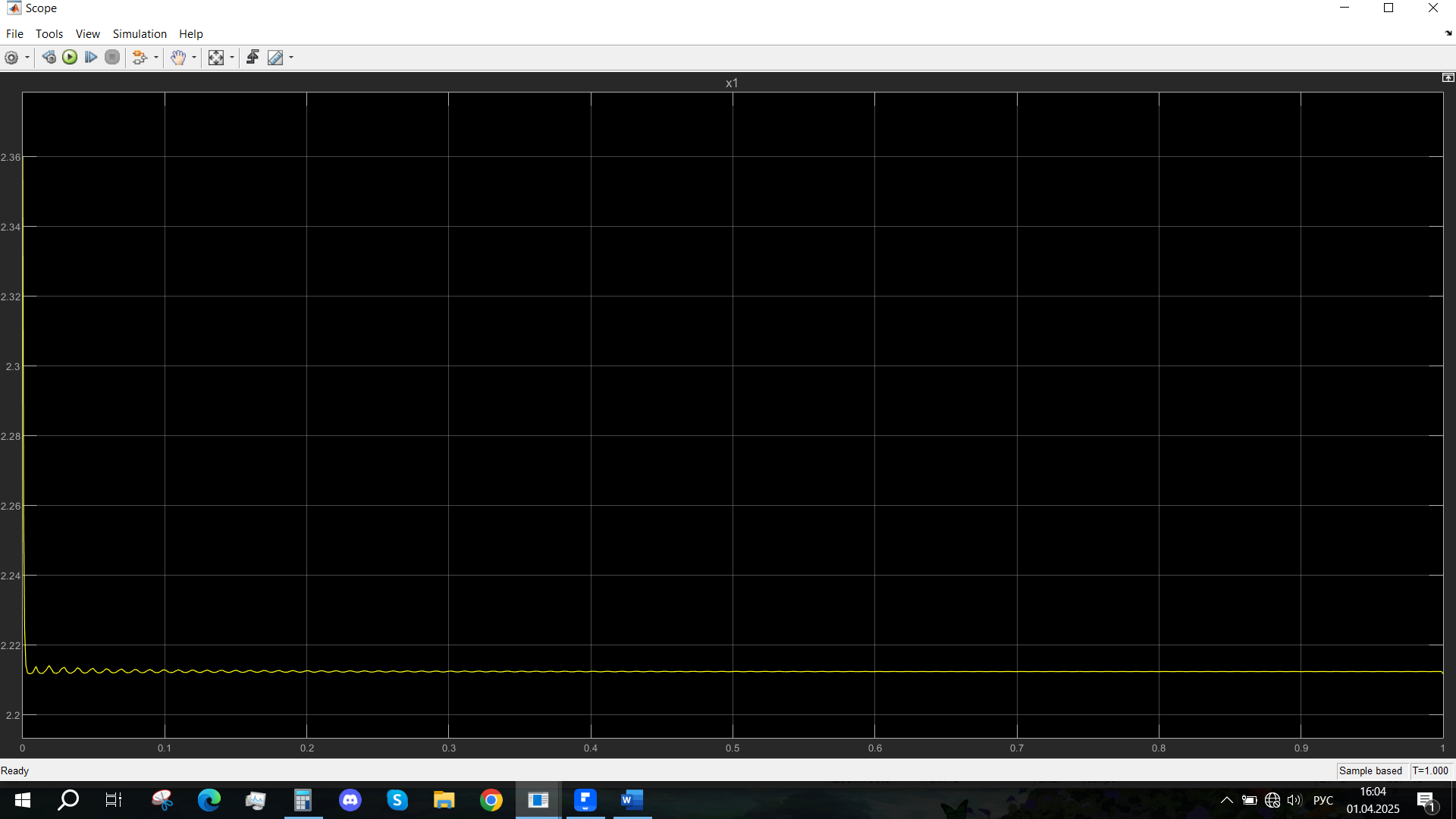
Рис. 56 - Переходная характеристика Uvn

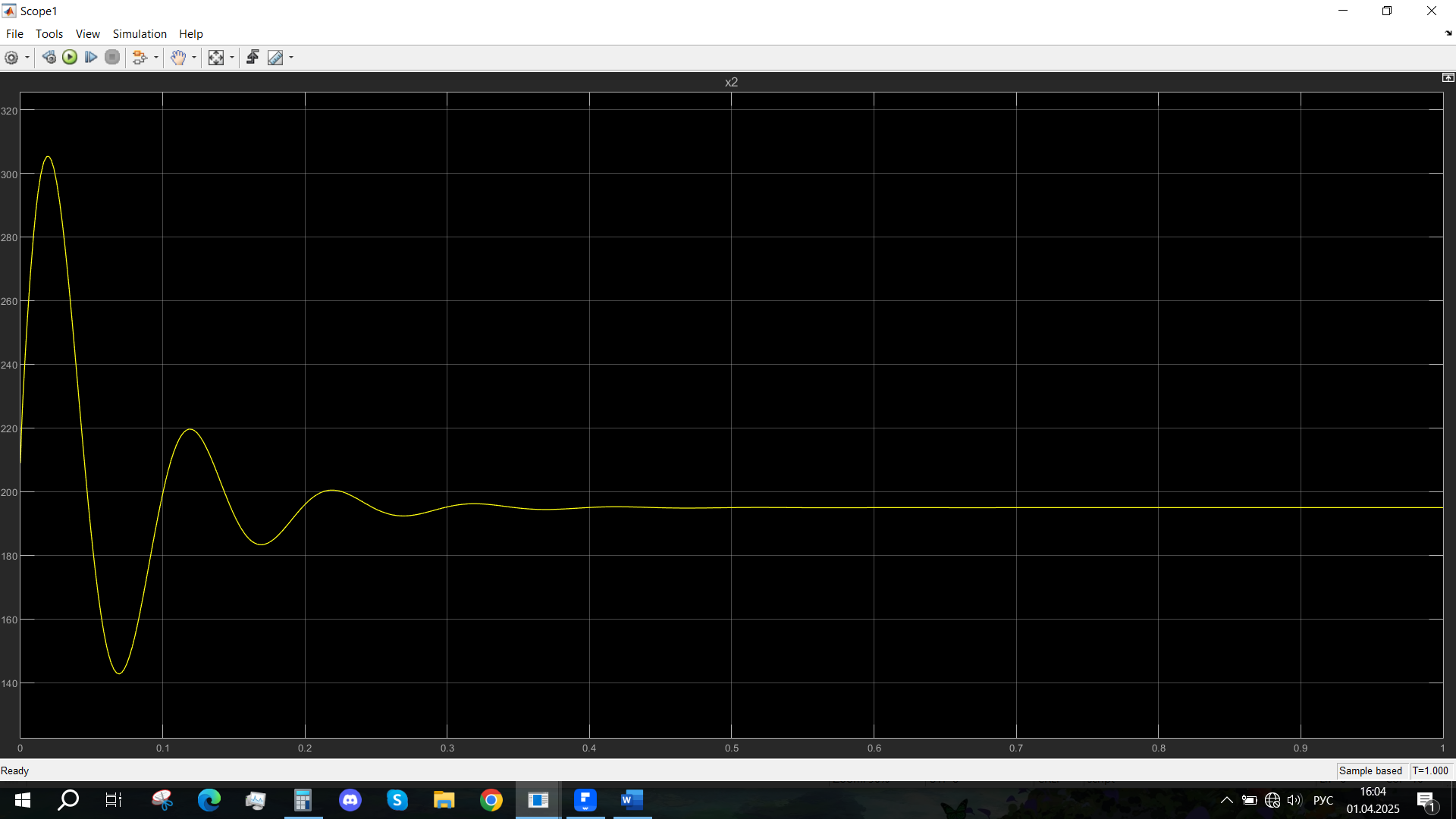
Рис. 57 - Переходная характеристика Ucn

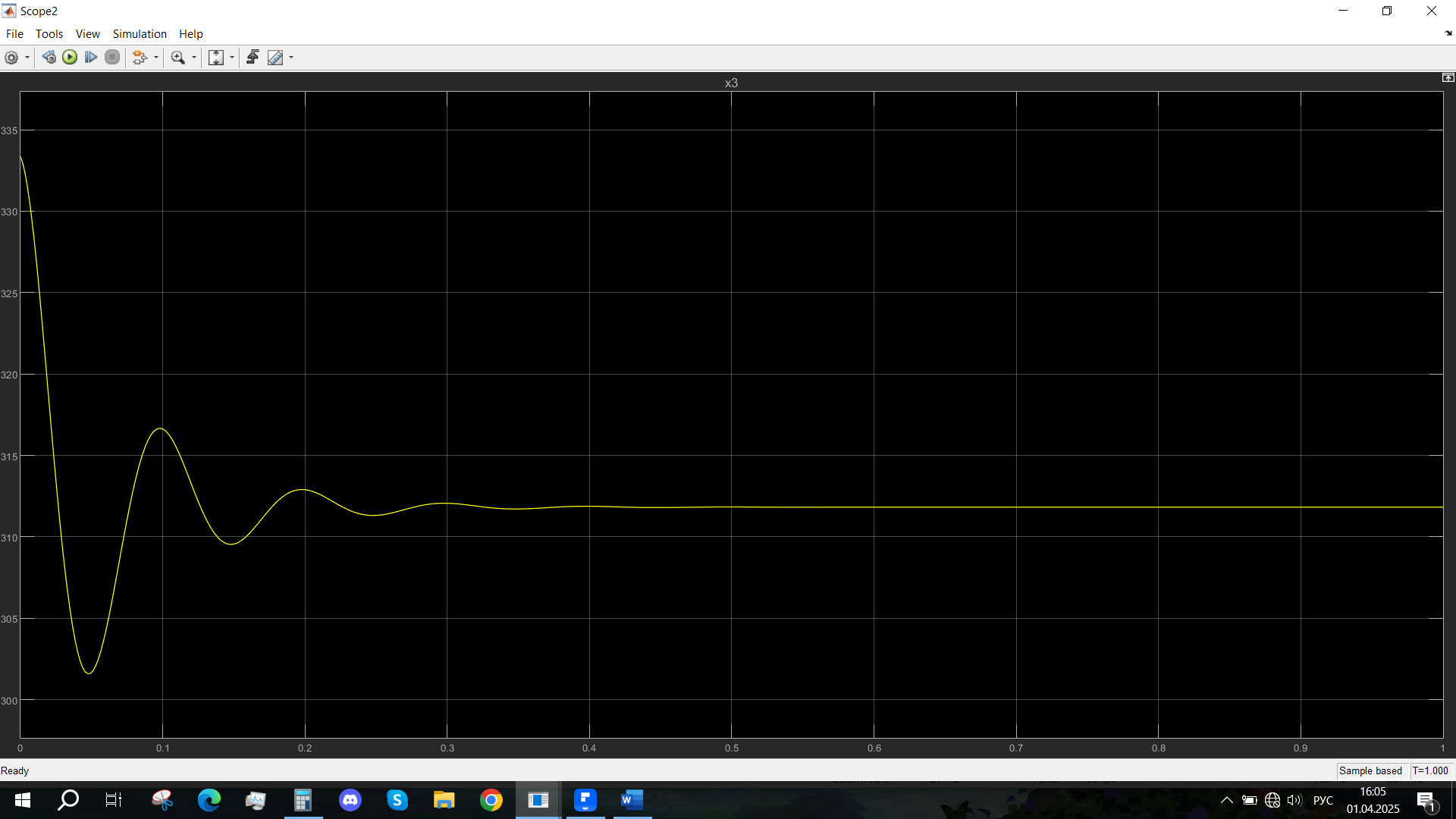
Рис. 58 - Переходная характеристика Mvn

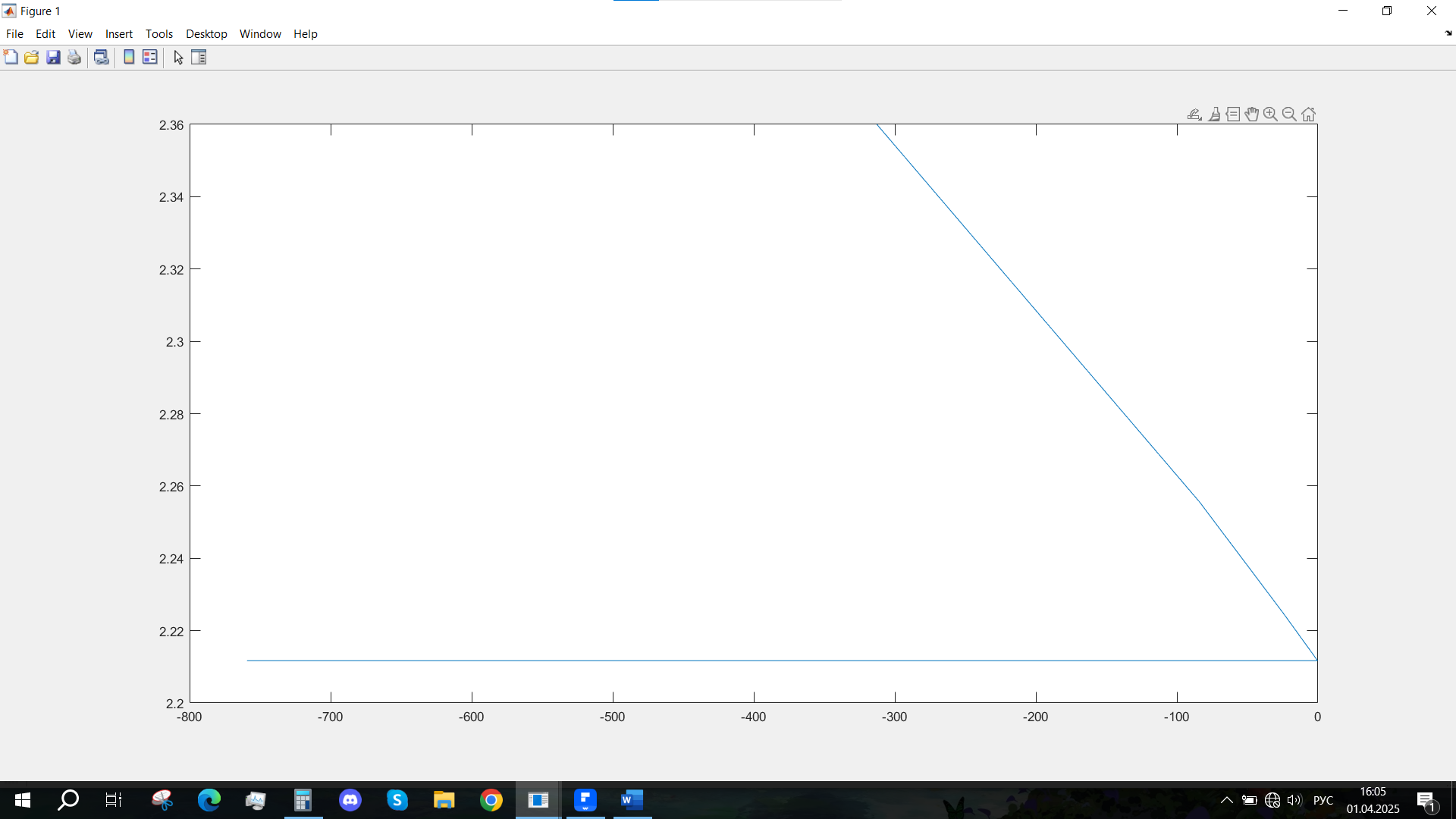
Рис. 59 - Фазовый портрет Uvn

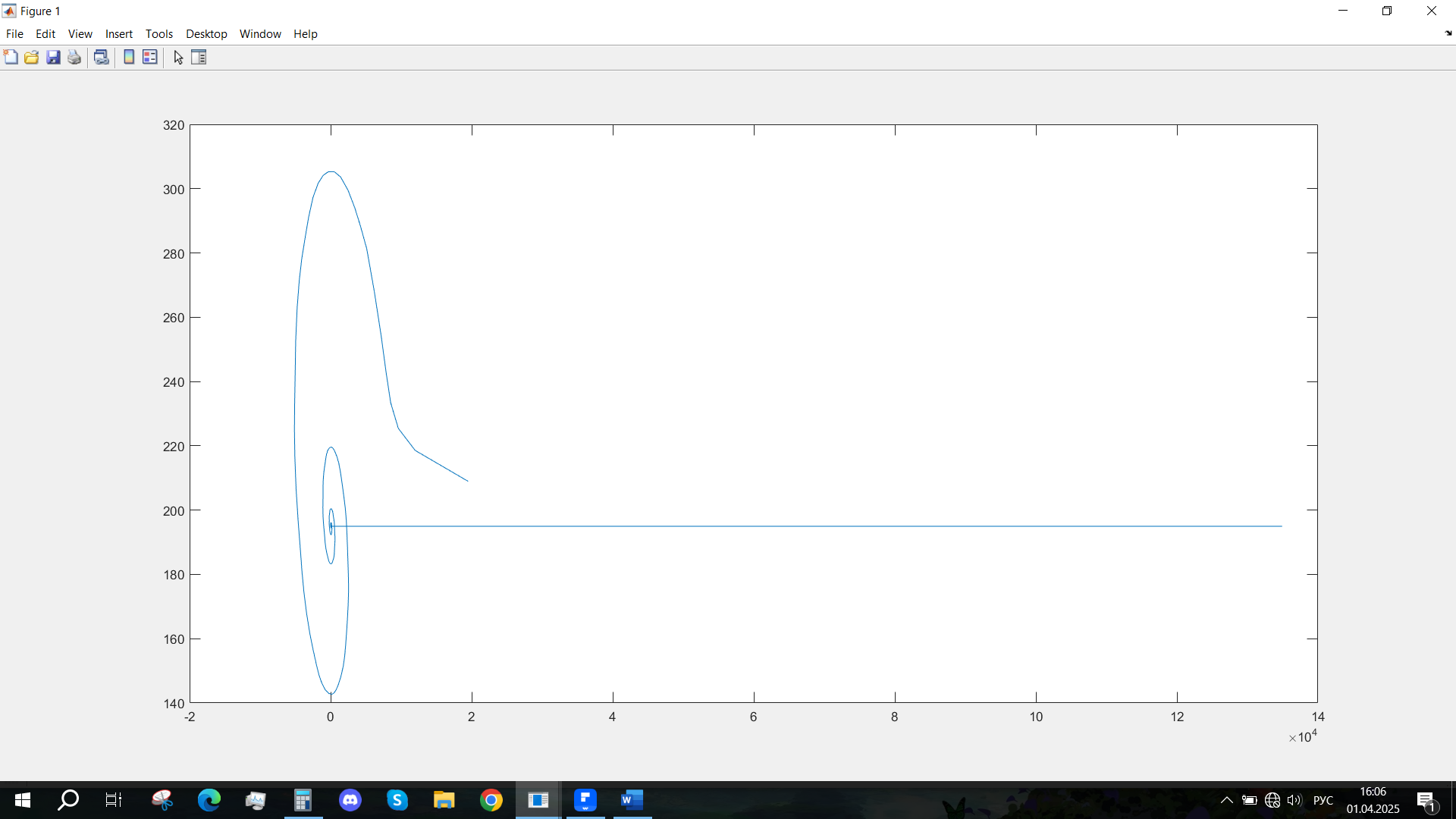
Рис. 60 - Фазовый портрет Ucn

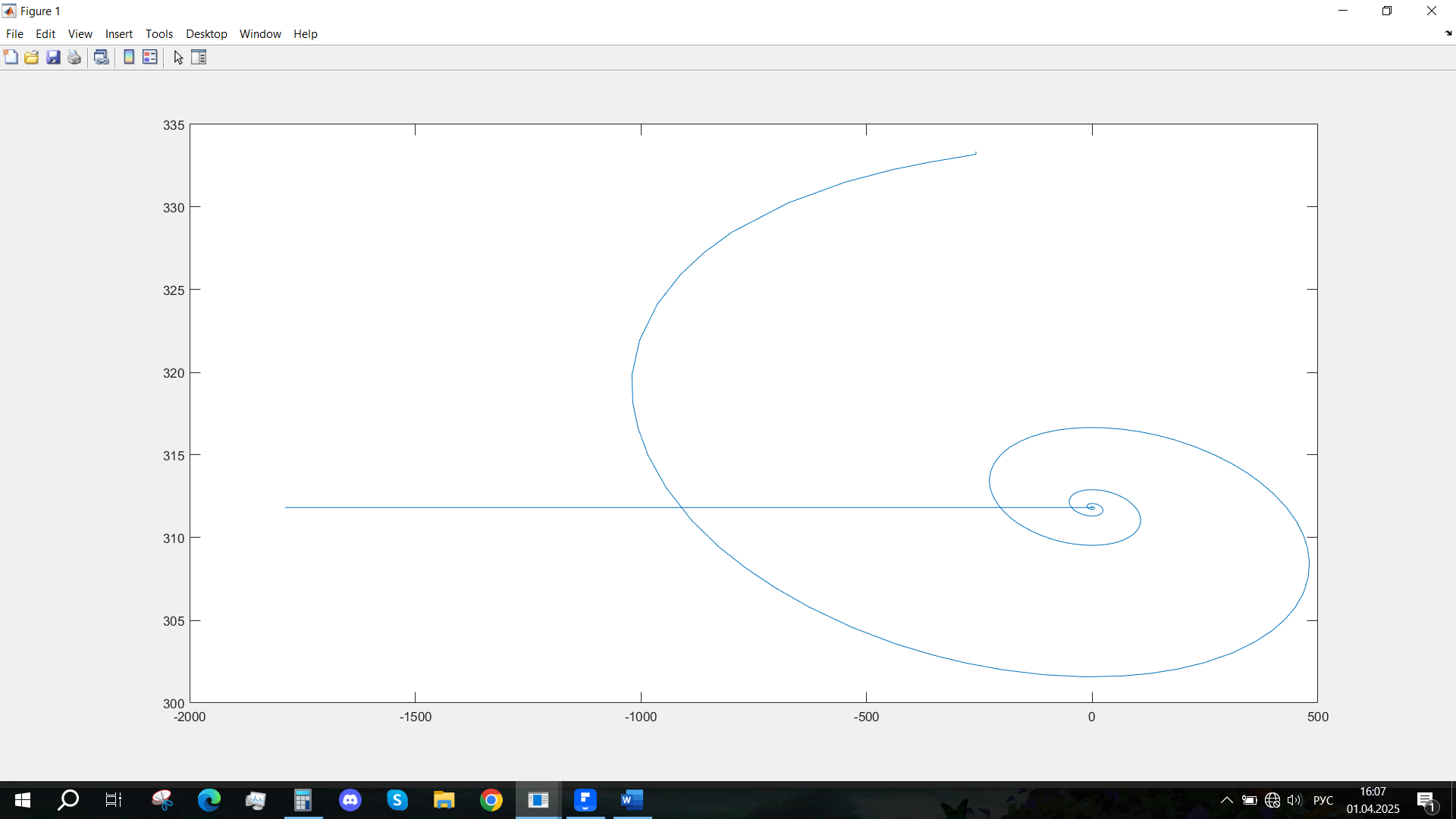
Рис. 61 - Фазовый портрет Mvn

Вывод: в ходе выполнения лабораторной работы были исследованы характеры переходных процессов при помощи численного интегрирования СНДУ объекта, была построена модель динамической системы в среде SIMULINK, были построены переходные процессы и фазовые портреты для всех переменных состояния при номинальных входных переменных, а также при отклонениях воздействий u1, u2, u3.