Лабки-лапки / Lab_4_2

МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

Кафедра КСУ

ОТЧЕТ

по лабораторной работе № 4

по дисциплине «Моделирование систем управления»

Тема: . ИССЛЕДОВАНИЕ ЛИНЕАРИЗОВАННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

Вариант 2

Студенты гр. 1487		Томозов Г. Н. Сластин Н. Ю.
Преподаватель		Лукомская О. Ю.

Санкт-Петербург

2025

Цель: Провести линеаризацию СНДУ в окрестности статического режима, получить линеаризованную математическую модель, описывающую динамику системы при малых отклонениях входных переменных от рассматриваемого статического режима; исследовать линеаризованную модель на ее соответствие нелинейной модели; исследовать устойчивость системы и характер переходных процессов.

Исходные данные:

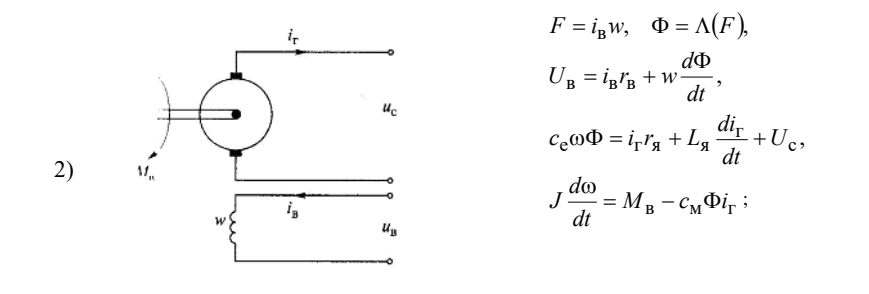
Таблица 1. Параметры объектов моделирования

Таблица 2. Входные, выходные и нормировочные параметры

Таблица 3. Кривые намагничивания.

Матрица состояния определяется следующим образом:

Аналогичным образом определяются:

B=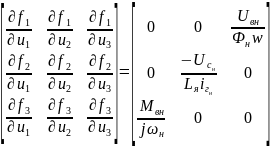

Матрица выхода:

Рис.1 – Схема Simulink

Рис.2 – Подсистема Simulink линеаризованной системы

z

Рис.3 – Подсистема Simulink нелинейной системы

Код программы:

J = 0.12;

wn = 100;

Cm = 200;

potokn = 0.005;

In = 50;

Mvn = 70;

Lya=0.01;

Ucn = 220;

Uvn = 220;

Ce = 205;

ra = 0.3;

w = 4000;

rb = 145;

rv = 145;

Fn = (Ucn*w)/rv;

rw = 145;

rja = 0.3;

w = 4000;

Lja = 0.01*1000;

R0 = 4;

ce = 205;

cm = 200;

J = 0.35;

Fn = 0.007;

Wn = 100;

in = 50;

Mvn = 70;

Uvn = 220;

F = Uvn/rw*w;

a11 = 1/(w*Fn)*(-rw*F/w);

a12 = 1/(w*Fn)*Uvn;

a21 = 1/(Lja*in)*ce*Fn*Wn;

a22 = 1/(Lja*in)*(-in*rja);

a23 = 1/(Lja*in)*(-in*R0);

a31 = 1/(J*Wn)*Mvn;

a32 = 1/(J*Wn)*(-cm*Fn*in);

c5 = 0.7479; c3 = -0.1896; c1 = 0.5022;

u1 = 1; u2 = 1; u3 = 1;

x10 = 0.983; x20 = 1.018; x30 =1.55;

A11=a11*(5*c5*x10^4+3*c3*x10^2+c1);

A12=0;

A13=0;

A21=a21*x30;

A22=a22+a23*u3;

A23=a21*x10;

A31=a32*x20;

A32=a32*x10;

A33=0;

B11=a12;

B23=a23*x20;

B32=a31;

x100=0.983;

x200=1.018;

x300=1.55;

u1=1;

u2=1;

u3=1;

du1=u1-u1;

du2=u2-u2;

du3=u3-u3;

Дальше всё из примера там не по нашему варику

Переходные процессы для различных режимов в сравнении с нелинейной системой из ЛР №2

Рис.1 Переходные процессы при отклонении от номинального режима по Uc на -20% для величины Ф.

Рис.2 Переходные процессы при отклонении от номинального режима по Uc на -20% для величины ir.

Рис.3 Переходные процессы при отклонении от номинального режима по Uc на -20% для величины w.

График расположения корней полинома на комплексной плоскости представлен на рис. 4:

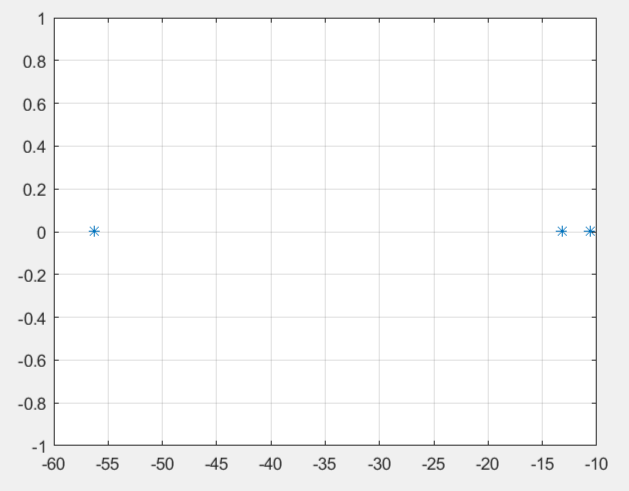
Рис.4 Корни ХП

Как видно из рис. 4, у всех корней вещественная часть находиться в левой полуплоскости, что говорит об асимптотической устойчивости системы.

Численные показатели матриц частных производных:

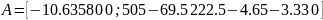
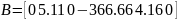
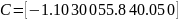
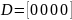
Выводы:

В ходе лабораторной работы была проведена линеаризация СНДУ в окрестности статического режима, в результате которой была получена матрица математической модели. По полученным переходным процесса можно сказать о соответствии линеаризованной модели нелинейной в окрестности статического режима. По найденным корням характеристического полинома матрицы A можно сказать, что система устойчива.