Исследование статических режимов динамической системы
Цель: преобразовать исходную систему уравнений в СНЛАУ, описывающую статические режимы, рассчитать статические характеристики динамической системы с помощью языка Matlab.
Статический режим динамической системы – это ее равновесное состояние, соответствующее окончанию переходных процессов. Например, изменение напряжения возбуждения на новое постоянное значение вызывает изменение МДС, магнитного потока, тока и напряжения генератора и т.д. Переходный процесс заканчивается новыми установившимися значениями этих величин, т.е. новым статическим режимом. Статический режим будет описывать система алгебраических уравнений, т.е. уравнений, куда не входят производные, так как последние в статическом режиме равны нулю.
Все статические режимы могут быть описаны СНЛАУ, записанной в обобщенной форме относительно компонент векторов и и х:
Математическая модель ГПТ НВ, работающего на сеть большой мощности.
Запишем исходную систему уравнений, описывающую наш ГПТ НВ.
Запишем данную систему в установившемся режиме (все производные равны нулю).
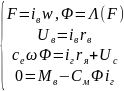
Выразим нашу систему через переменные состояния.
Переменные
состояния в нашей модели:
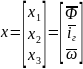Входные
переменные в нашей модели:
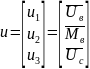
Выразим
ток нагрузки через ток якоря:
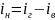
Выражаем
ток возбуждения через полином, найденный
в лабораторной работе №1:
,
.
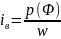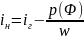В исходной системе уравнений выразим производные по переменным состояния и подставим выражения для тока нагрузки и тока возбуждения:
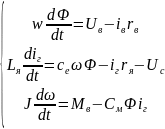
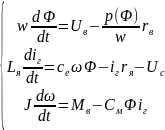
Приравниваем производные к нулю:
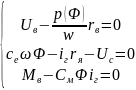
Преобразуем систему уравнений:
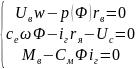
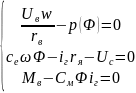
Перепишем данную систему через отнормированные параметры:
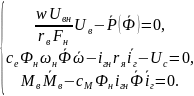
Запишем
систему через переменные состояния,
полученные выше:
.
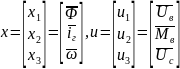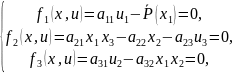
Вводим коэффициенты:
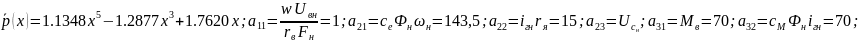
Переписываем нашу систему уравнений:
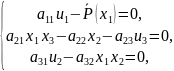
В данном случае наша система решается методом Ньютона. Для этого нам нужна следующая матрица:
G(x,u)=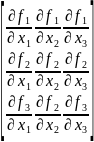
Это матрица частных производных.
Заполняем матрицу:
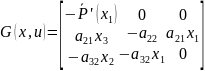
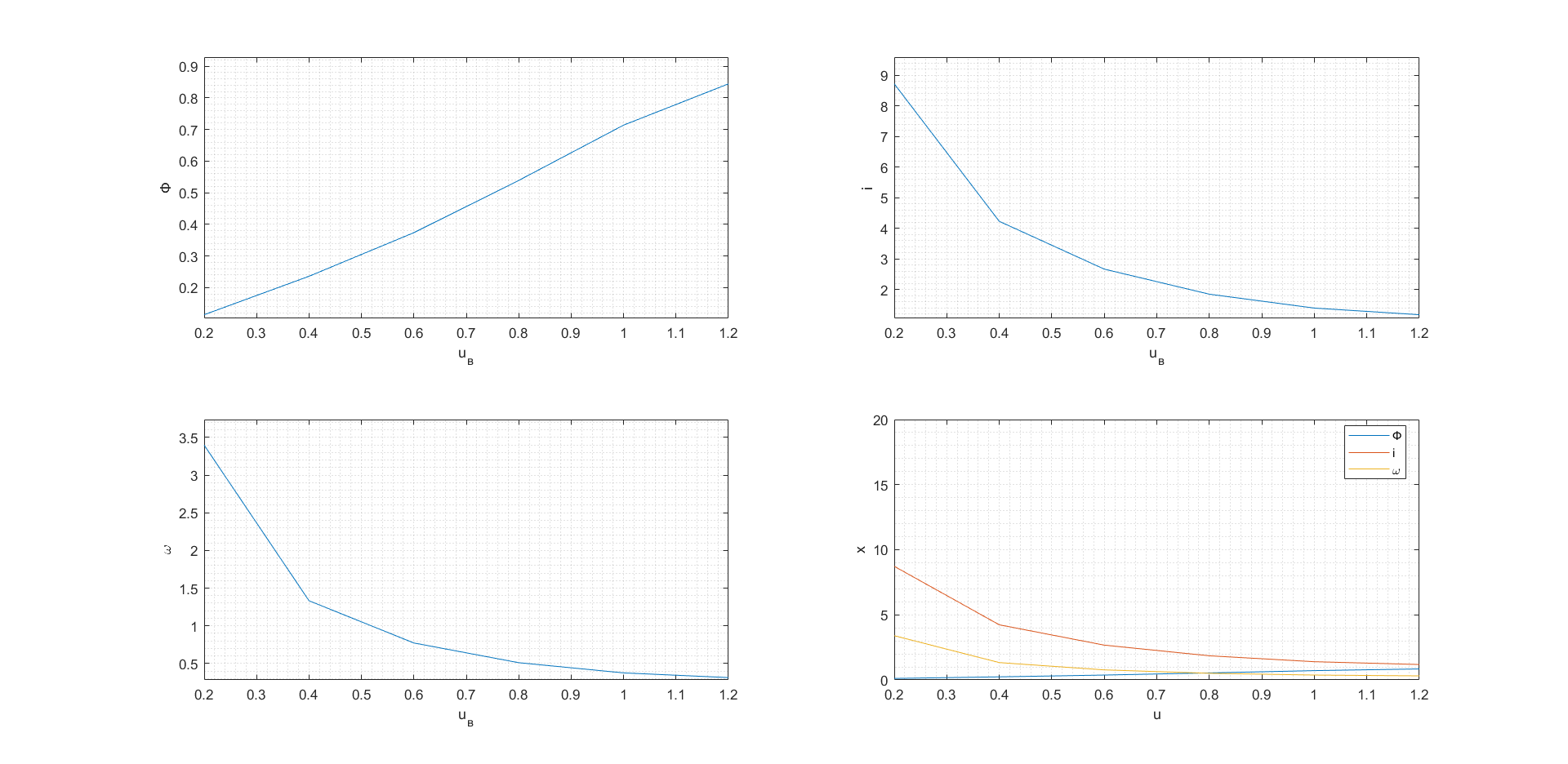
Рис. 64. Статические характеристики при изменении параметра u1 (0.05, 1.2)
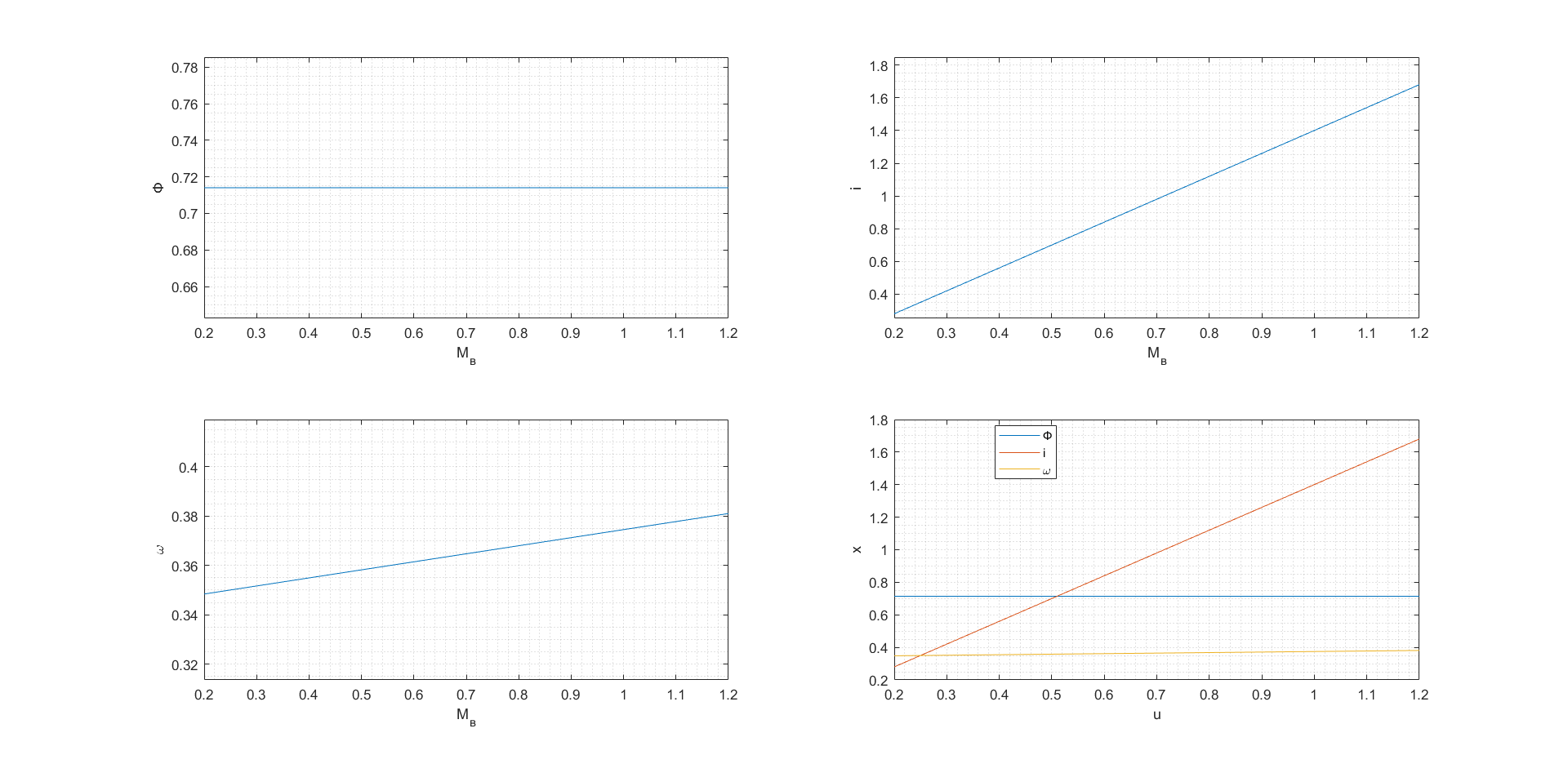
Рис. 65. Статические характеристики при изменении параметра u2 (0.05, 1.2)
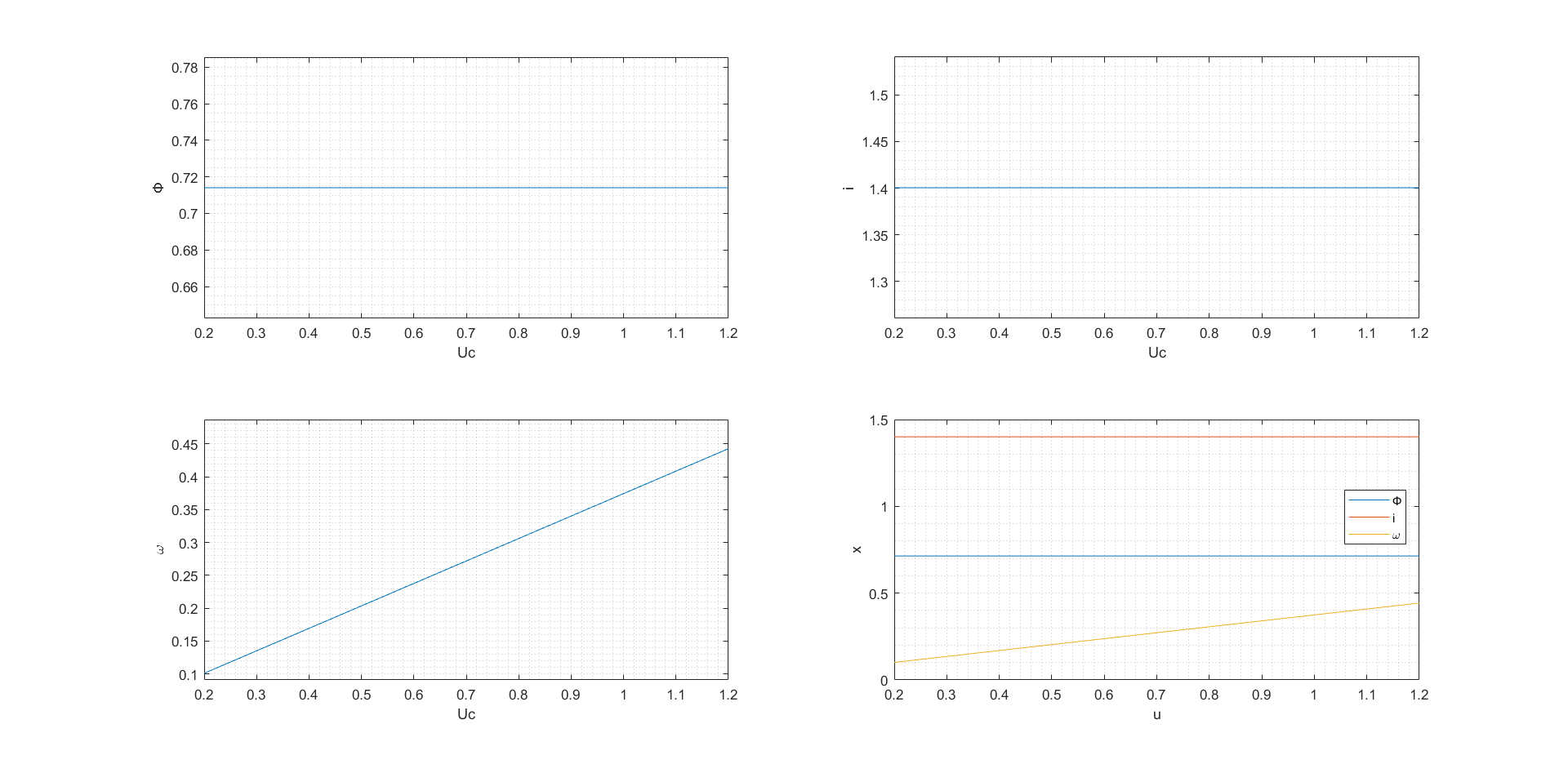
Рис. 66. Статические характеристики при изменении параметра u3 (0.05, 1.2)
Выводы.
В ходе выполнения данной лабораторной работы использовалась система уравнений СНЛАУ, описывающая статические режимы:
В качестве функции обратной кривой намагничивания использовался нормированный полином 5-й степени, найденный в предыдущей работе:
Также
с помощью Matlab
были рассчитаны и построены статические
характеристики нашей системы, кроме
того, были найдены значения переменных
состояния в установившемся режиме:
.
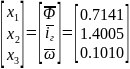Исследование линеаризованной математической модели
Цель: провести линеаризацию СНДУ в окрестности статического режима, получить линеаризованную математическую модель, описывающей динамику системы при малых отклонениях входных переменных от рассматриваемого статического режима; исследовать линеаризованную модель на её соответствие нелинейной модели; исследовать устойчивость системы и характер переходных процессов.
Аналитическое выражение матриц A, B, C, D.
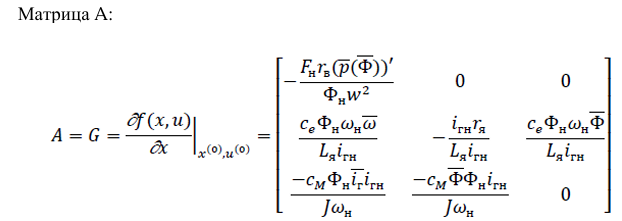
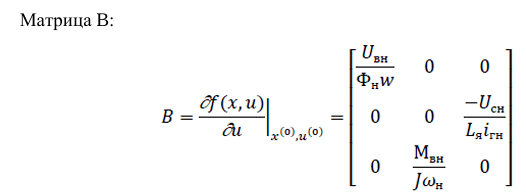
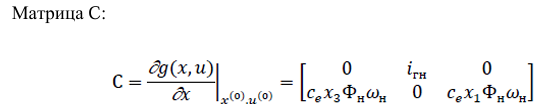
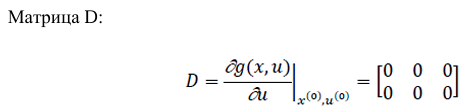
2. Рассчитаем значения коэффициентов матриц для статического режима Зададим вектор состояния в окрестности номинального статического режима.
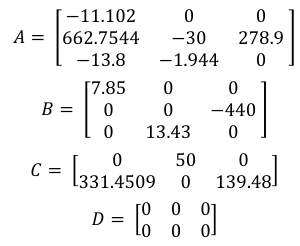
3.Рассчитаем переходные процессы и построим графики перехода из статического режима (𝑢0,𝑥0) в статический режим (𝑢1,𝑥1)
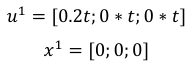
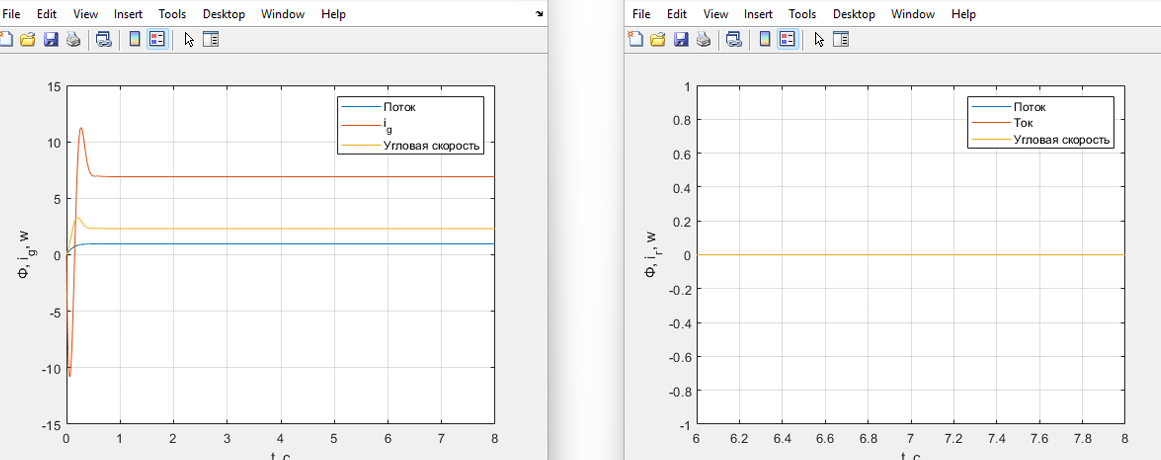
Рисунок 67 – номинальный режим в нелинейной системе (слева) и в линеаризованной (справа)
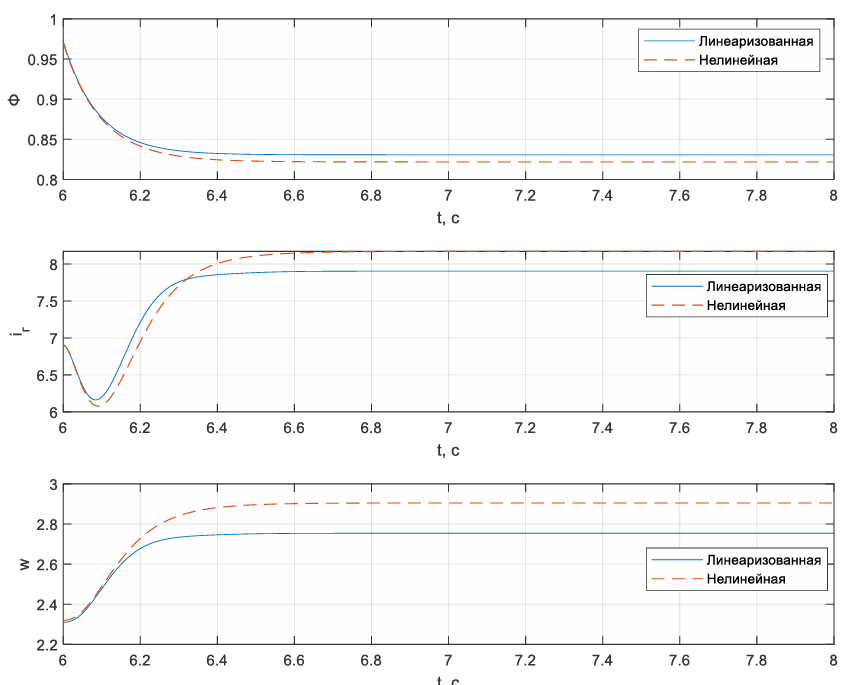
Рисунок 67 – изменение входа u(1) статического режима в -20% для линеаризованной и нелинейной системы
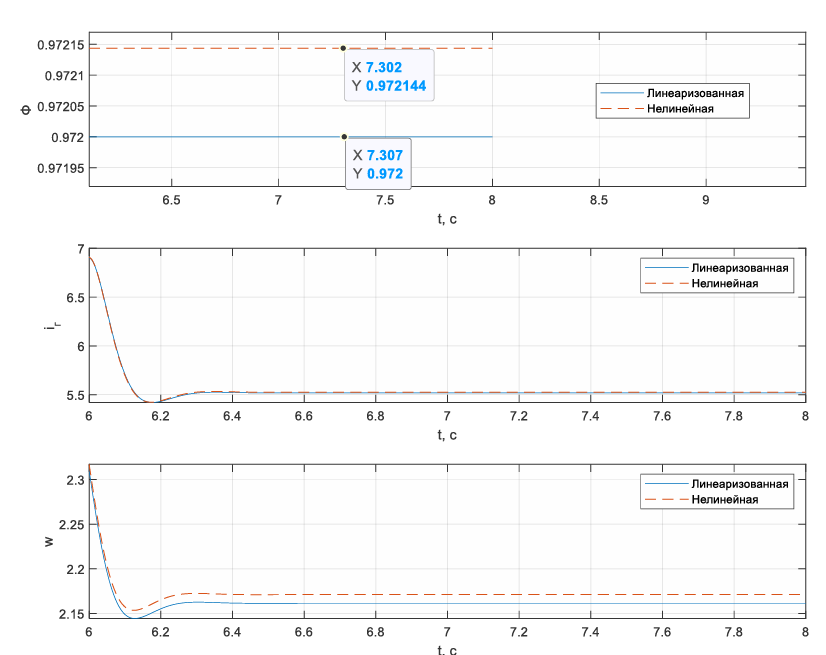
Рисунок 68 – изменение входа u(2) статического режима в -20% для линеаризованной и нелинейной системы
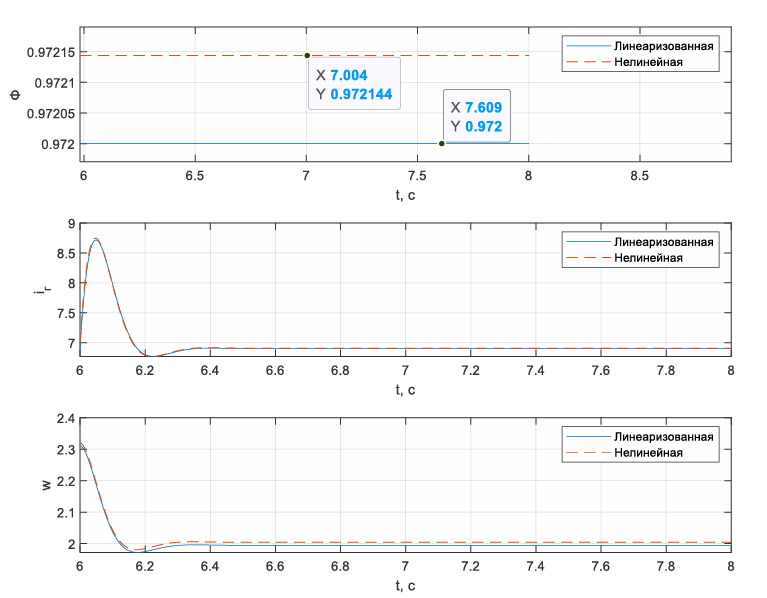
Рисунок 69 – изменение входа u(3) статического режима в -20% для линеаризованной и нелинейной системы
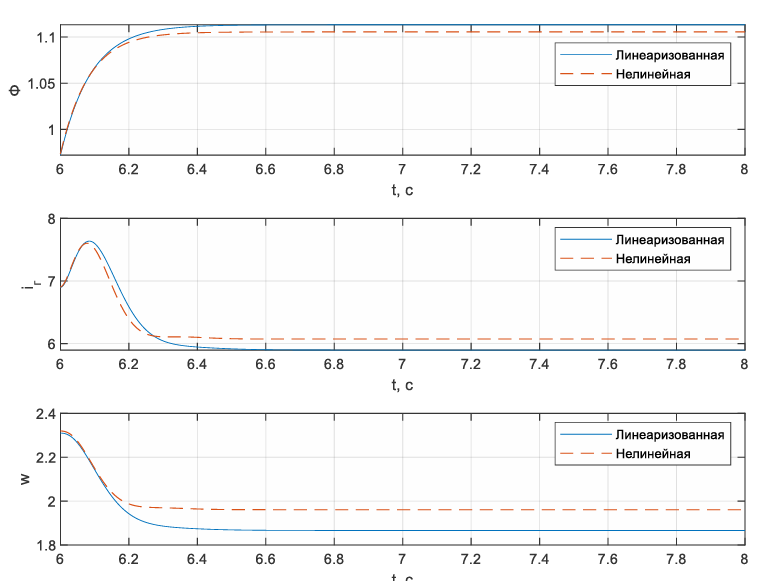
Рисунок 70 – Графики изменения входа u(1) статического режима в +20% для линеаризованной и нелинейной системы
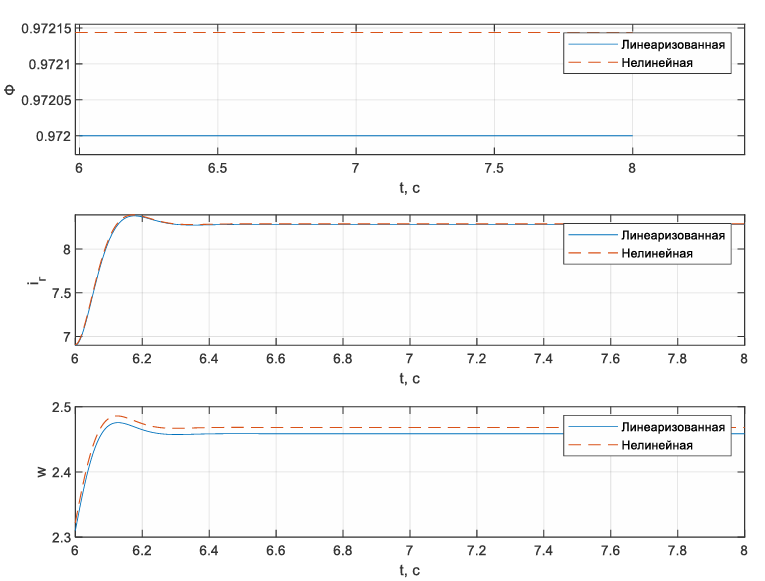
Рисунок 71 – Графики изменения входа u(2) статического режима в +20% для линеаризованной и нелинейной системы
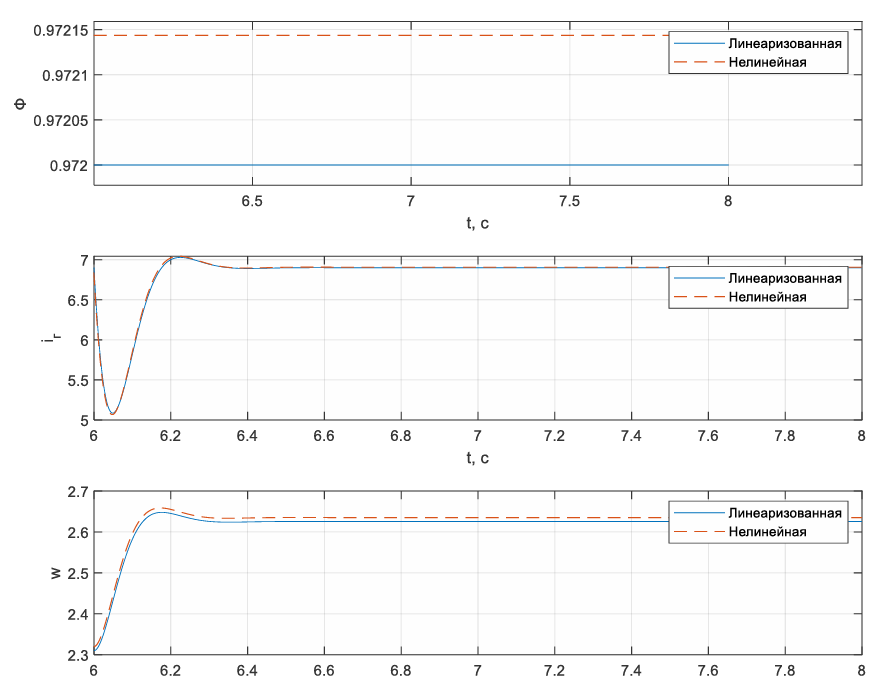
Рисунок 72 – изменение входа u(3) статического режима в +20% для линеаризованной и нелинейной системы
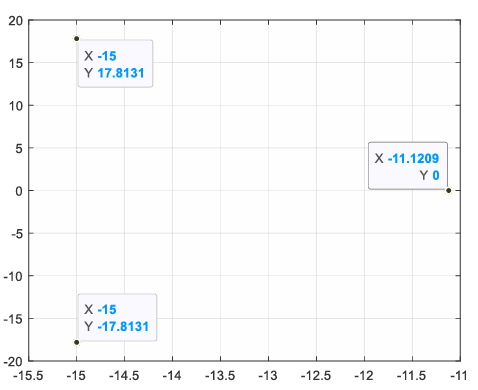
Рисунок 73 – Корни ХП на комплексной плоскости
Вывод: В ходе выполнения данной лабораторной работы была проведена линеаризация СНДУ в окрестности статического режима, получена линеаризованная математическая модель, описывающая динамику системы при малых отклонениях входных переменных от рассматриваемого статического режима, также исследована линеаризованную модель на ее соответствие нелинейной модели, результаты оказались очень близки.