ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

д-р физ.-мат. наук				Рождественский Ю.В
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №3

ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ МЕТОДОМ МОНТЕ -КАРЛО

по курсу: ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	4116
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2024

Цель работы: изучение метода Монте-Карло, определение точности вычисления определённых интегралов методом Монте-Карло.

Исходная функция

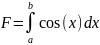
Ход работы:

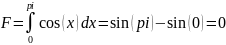
Написан код для реализации метода Монте-Карло, который применяется для вычисления интеграла функции cos(x) на интервале [0,π], также построен график для визуализации зависимости точности от количества случайных точек.

Для реализации метода Монте-Карло на заданном интервале интегрирования создаются N равномерно распределенных случайных точек. Для каждой точки вычисляется значение функции cos(x). Далее находится среднее значение всех вычисленных значений функции. Итоговое значение интеграла получается умножением среднего значения функции на длину интервала (b−a)

Точность метода оценивалась путём изменения количества случайных точек N.

Листинг 1- Вычисление интеграла методом Монте-Карло

import numpy as np

import matplotlib.pyplot as plt

def f(x):

return np.cos(x)

def monte_carlo_integration(a, b, n):

random_points = np.random.uniform(a, b, n)

function_values = f(random_points)

average_value = np.mean(function_values)

integral = (b - a) * average_value

return integral

a = 0

b = np.pi

n = 10000

result = monte_carlo_integration(a, b, n)

n_points = []

results = []

exact_value = np.sin(np.pi) - np.sin(0)

# пробег по различным значениям количества точек

for n in range(50, 10000, 10):

result = monte_carlo_integration(a, b, n)

n_points.append(n)

results.append(result)

plt.figure(figsize=(10, 5))

plt.plot(n_points, results, label="Монте-Карло")

plt.axhline(y=exact_value, color='r', linestyle='--', label="Точное значение")

plt.xlabel("Количество точек N")

plt.ylabel("Приближённое значение интеграла")

plt.title("График зависимости приближенного значения интеграла от количества точек")

plt.legend()

print(f"Приближённое значение интеграла cos(x) от 0 до pi методом Монте-Карло: {result}")

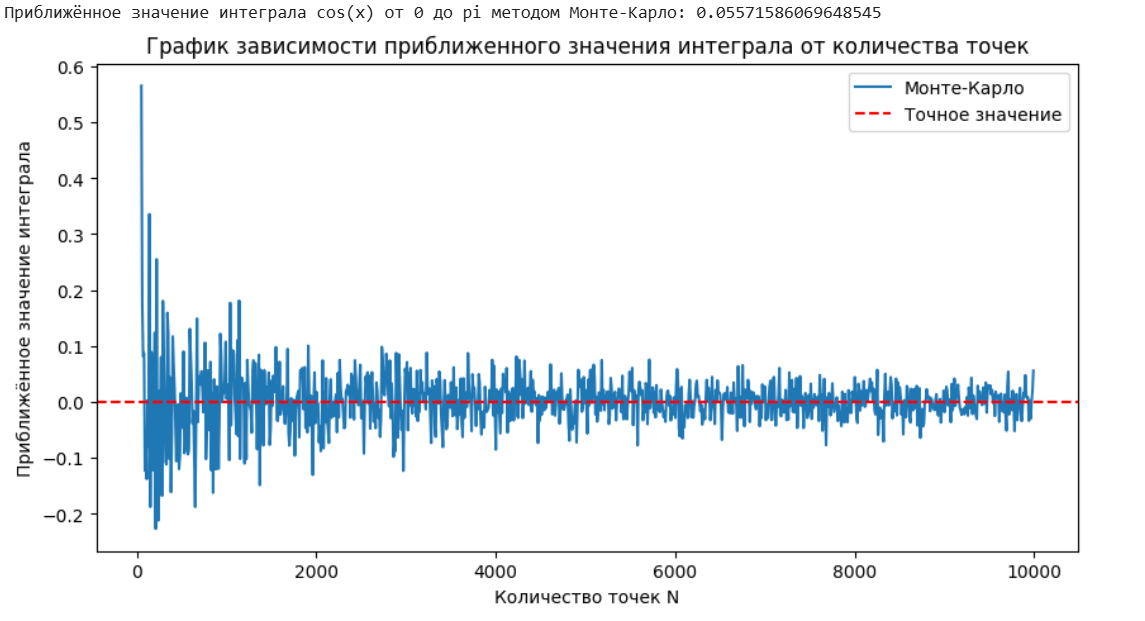
Рисунок 1 – Графическое представление моделирования

Можно сделать вывод, что точность метода зависит от количества используемых случайных точек, с увеличением N приближение становится более точным.

Выводы: изучен метод Монте-Карло, определена точности вычисления определённых интегралов методом Монте-Карло. Построен график зависимости приближенного значения интеграла от количества точек.