ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

Старший преподаватель				Е.П. Виноградова
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1

ЗАДАЧА О СЧАСТЛИВОМ БИЛЕТЕ

по курсу: УЧЕБНАЯ ПРАКТИКА

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4116
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2022

Цель: решить данную задачу, как аналитически , так и с помощью программирования.

Условие задачи:

123456- номер 1-го билета. Всего было продано 900 билетов. Кондуктор думает, что билет будет считаться счастливым, если: сумма первых трёх цифр равна сумме последних трёх (1+2+3=4+5+6). Но водитель считает , что билет счастливый, если сумма цифр на нечётных позициях равна сумме цифр на чётных позициях (1+3+5=2+4+6).

Каков номер последнего билета? Сколько билетов оказалось счастливыми а) по мнению кондуктора; б) по мнению водителя ; в) по мнению и кондуктора и водителя; г) сколько билетов вообще не счастливые.

Решение: чтобы вычислить номер последнего билета, нужно: номер первого билета + (проданное количество билетов -1) , получаем, 123456+899=124355- номер последнего билета.

Вычислим сколько счастливых билетов по мнению кондуктора:

Первый три цифры всегда либо 123, либо 124, поэтому пусть номер первого билета 123456(abcdef), пусть a+b+c=d+e+f, тогда а=1, b=2,с=3,

1+2+3=6, значит, d+e+f должно равняться 6, это можно получить с помощью таких комбинаций , как (5+0+1, 6+0+0)

1+2+3=5+0+1(1)

1+2+3=5+1+0(1)

1+2+3=6+0+0(1)

Если a=1, b=2, c=4, тогда 1+2+4=7, получается d+e+f должно равняться 7.

Это можно получить с помощью таких комбинаций( 7+0+0, 4+3+0, 5+1+1, 5+2+0, 6+0+1, 4+1+2,

Воспользуемся формулами из комбинаторики

1+2+4= 3+4+0( на первом месте может стоять 3 и 0 , на втором месте 4 ,3 и 0 и на третьем тоже 4 , 3 и 0 , поэтому количество нужных нам чисел = 2*2*1=4)

1+2+4=0+0+7( 1*2*1=2)

1+2+4=0+1+6( 2*2*1=4)

1+2+4=0+2+5( 2*2*1=4)

1+2+4=0+3+4(2*2*1=4)

1+2+4=1+1+5(1*2*1=2)

1+2+4=1+2+4 ( 2*2*1=4)

1+2+4=1+3+3 (3*1*1=3)

1+2+4=2+2+3( 3*1*1=3)

Складываем всё и получаем: 29

по мнению кондуктора имеется 16 счастливых билетов.

Сколько счастливых билетов по мнению водителя можно посчитать также, с помощью комбинаторики.

Решение представлено на языке программирования Pascal:

program schastliviybilet;

var i,t,sum1,sum2,k ,b,c,d,e,f,g,sum3,sum4,m,n,l: integer;

a: array[0..900] of integer;

begin

a[0]:=123456;

k:=0;

for i:= 0 to 899 do

begin

a[i+1]:=a[i]+1;

b:=a[i] div 100000;

c:=a[i] div 10000 mod 10;

d:= a[i] div 1000 mod 10;

e:= a[i] div 100 mod 10;

f:= a[i] div 10 mod 10 ;

g:= a[i] mod 10;

sum1:=b+c+d; sum2:= e+f+g;

sum3:=b+d+f; sum4:=c+e+g;

if sum1=sum2 then k:=k+1;

if sum3=sum4 then m:=m+1;

if (sum1=sum2) and (sum3=sum4) then n:=n+1;

if (sum1<>sum2) and(sum3<>sum4) then l:=l+1;

t:=a[i]

end;

writeln('номер последнего билета ',t);

writeln('количество счастливых билетов по мнению кондуктора',k);

writeln('количество счастливых билетов по мнению водителя ', m);

writeln('количество счастливых билетов по мнению двух ', n );

writeln('количество вообще не счастливых билетов ', l);

end.

Снимок результата работы программы:

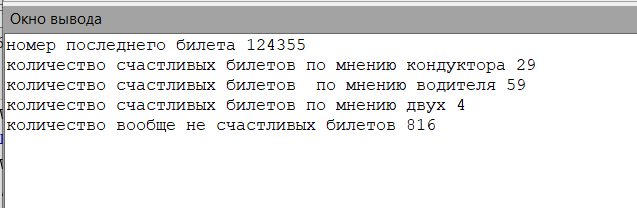
Вывод: аналитически данный тип задач решается долго и есть большая вероятность ошибки, поэтому задания такого типа лучше всего решать с помощью программирования.