ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

Старший преподаватель				Б.К.Акопян
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1

НАХОЖДЕНИЕ ПРОИЗВОДНОЙ СЛОЖНОЙ ФУНКЦИИ

по курсу: ПРИКЛАДНЫЕ МЕТОДЫ ОТПТИМИЗАЦИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	4116
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2024

Цель работы: закрепление навыков вычисления производных сложных функций, изучение возможностей среды MathCAD в применении к вычислению производной сложной функции.

Вариант 4:

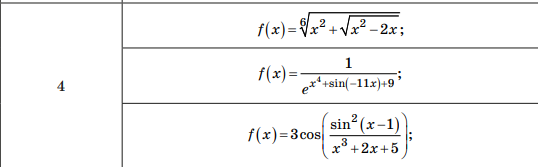
Рисунок 1- Вариант индивидуального задания

Ход работы:

Вычислена производная первой функции вручную.

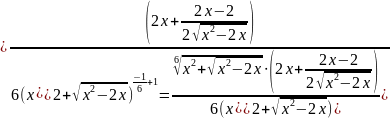
Затем производная вычислена в Mathcad (Рисунок 2).

Рисунок 2- Решение первой производной

Результат решения вручную и в Mathcad совпали.

Произведено решение второй производной вручную и в Mathcad (Рисунок 3).

Рисунок 3- Решение второй производной

Результаты решений второй производной разными способами совпали.

Затем решена третья производная аналитическим способом.

;

Ответ, полученный аналитическим способом, совпал с ответом в Mathcad (Рисунок 4).

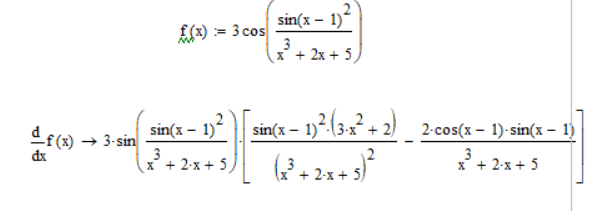
Рисунок 4 - Решение третьей производной в Mathcad

Вычислена четвертая производная аналитическим способом и в Mathcad (Рисунок 5).

+ = + +

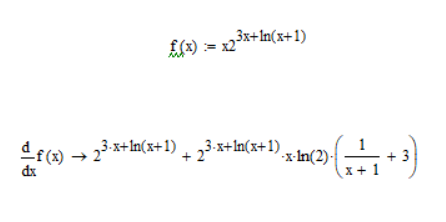
Рисунок 5- Решение четвертой производной в Mathcad

Вычислена пятая производная (Рисунок 6).

= );

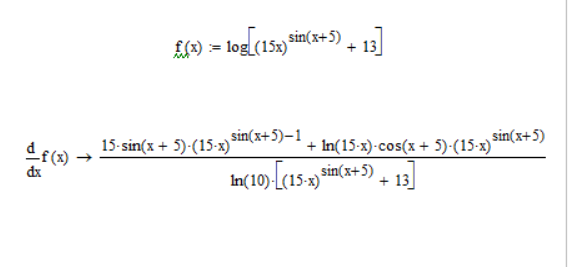
Рисунок 6- Решение пятой производной в Mathcad

Произведены вычисления шестой производной (Рисунок 6).

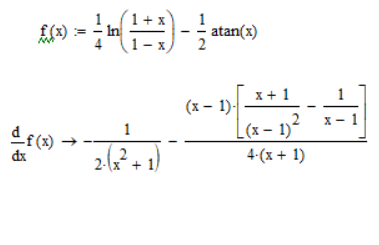
Рисунок 7- Решение шестой производной в Mathcad

Вычислена седьмая производная (Рисунок 8)

Рисунок 8-Решение седьмой производной в Mathcad

Вывод: вычислены производные сложных функций, изучены возможности среды MathCAD в применении к вычислению производной сложной функции.