ГУАП

КАФЕДРА ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ И СЕТЕЙ

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

Старший преподаватель				Д.В. Куртяник
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1

ПЕРЕДАЧА ФУНКЦИЙ В КАЧЕСТВЕ ПАРАМЕТРОВ. ПЕРЕГРУЗКА ФУНКЦИЙ.

по курсу: ОСНОВЫ ПРОГРАММИРОВАНИЯ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4116
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2022

Цель лабораторной работы: изучение методов передачи имён функций в качестве параметров других функций; изучение перегрузки функций; совершенствование навыков программирования на языке С++.

Задание на программирование: найти площадь между двумя линиями используя численное интегрирование.

Вариант 23: y = 4 − x², y = 3x.

Ход работы:

Графики функций: парабола 𝒚= 4-x² и прямая 𝑦=3𝑥. Ветви параболы направлены вниз и парабола пересекает абсциссу в точках 𝑥=-2, 𝑥=2. Прямая пересекает абсциссу в точке начала координат.

Площадь фигуры, ограниченной линиями, вычисляется с помощью определённого интеграла.

S=

График параболы располагается выше графика прямой. Значит, 𝑓(𝑥)= 4-x², 𝑔(𝑥)=3x. Граница интегрирования 𝑎 и 𝑏 – это точки пересечения графиков функций. Графики функций пересекаются в точках, где значения функций равны (𝑓(𝑥)=𝑔(𝑥)).

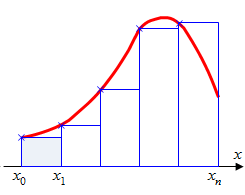
Для того, чтобы вычислить определённый интеграл, воспользуемся методом левых прямоугольников. Данный метод вычисления интеграла предполагает разбиение интервала интегрирования [a,b] на n отрезков с шагом h (h = ) и вычисления площади прямоугольников, где h умножается на значение функции в левой точке, полученные значения суммируются.

+…

Исходный код:

#include <iostream>

#include <cmath>

using namespace std;

double f1(double x) // описание линии 1

{

return(4 - pow(x, 2)) * 10 / 10.;

}

double f2(double x) //описание линии 2

{

return (3 * x) * 10 / 10.;

}

void peresechenie(double(f1(double x)), double(f2(double x))) //нахождение точек пересечения линий с осью х

{

int count = 0;

for (int i = -10; i<= 10; i++)

{

if (f1(i) == 0)

{

count++;

cout << "точка пересечения линии 1 с осью х : " << i<< endl;

}

if (f2(i) == 0)

{

count++;

cout << "точка пересечения линии 2 с осью х : " << i<< endl;

}

}

}

void peresechenie(double(f1(double x)), double(f2(double x)), double& tochka1, double& tochka2) // нахождение точек пересечения линий

{

int count = 0;

for ( double i = -10; i <=10; i++)

{

if ((f1(i) == f2(i)) && (count==0))

{

tochka1 = i;

count++;

cout <<" первая точка пересечения двух линий : " << tochka1<< endl;

}

else if ((f1(i) == f2(i)) && (count == 1))

{

tochka2 = i;

cout << "вторая точка пересечения двух линий : " << tochka2<< endl;

}

}

}

double integral(double(f(double x)), double& tochka1, double& tochka2) //численное интегрирование

{

int n = 1000;

double h = (tochka2 - tochka1) / n;

double s = 0.0;

for (int i = 0; i <= n-1; i++)

{

s += h * f ( tochka1 + i* h);

}

return s;

}

int main()

{

setlocale(LC_ALL, "RUS");

double tochka1, tochka2;

peresechenie(f1, f2);

peresechenie(f1, f2, tochka1, tochka2);

cout << "площадь между двумя линиями: " << integral(f1, tochka1, tochka2) - integral(f2, tochka1, tochka2) << endl;

return 0;}

Результат выполнения программы:

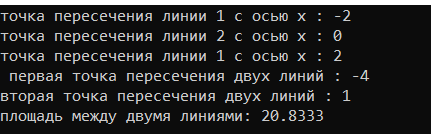
Сравнение результатов численного интегрирования в программе и точного аналитического решения, оценка погрешности.

Находим границы интегрирования:

𝑓(𝑥)=𝑔(𝑥)

4-x²=3x

x²+3x-4=0

x₁=-4; x₂=1

𝑆=

тогда, применив формулу Ньютона-Лейбница( )

≈ 20,8333

Погрешности в вычислениях минимальная.

Вывод: я изучила методы передачи имён функций в качестве параметров других функций, перегрузки функций и усовершенствовала навыки программирования на языке С++.