ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

старший преподаватель				Е.К. Григорьев
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №5

ПРОВЕРКА ПРОСТОЙ СТАТИСТИЧЕСКОЙ ГИПОТЕЗЫ О РАСПРЕДЕЛЕНИИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ ПРИ ПОМОЩИ КРИТЕРИЕВ СОГЛАСИЯ

по курсу: МОДЕЛИРОВАНИЕ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4116
				подпись, дата		инициалы, фамилия

Санкт-Петербург 2024

Цель работы: ознакомиться с существующими критериями согласия, получить навыки применения наиболее популярных критериев в современных математических пакетах.

Вариант 21 (1)

Ход работы

Часть 1

Выписаны интервалы, полученные в прошлой лабораторной работе, их середины и частота. Также выписаны значения длины интервала, выборочного среднего, дисперсии и среднеквадратичного отклонения (Рисунок 1).

Рисунок 1-Интервалы, длина интервала, выборочное среднее и СКО

В прошлой работе было предположено, что рассматриваемое распределение является нормальным. Сформируем нулевую гипотезу – выборка подчиняется нормальному закону распределения. Для проверки гипотезы используется критерий согласия Пирсона. Чтобы вычислить теоретические частоты, посчитаны z-оценки и ) (Рисунок 2).

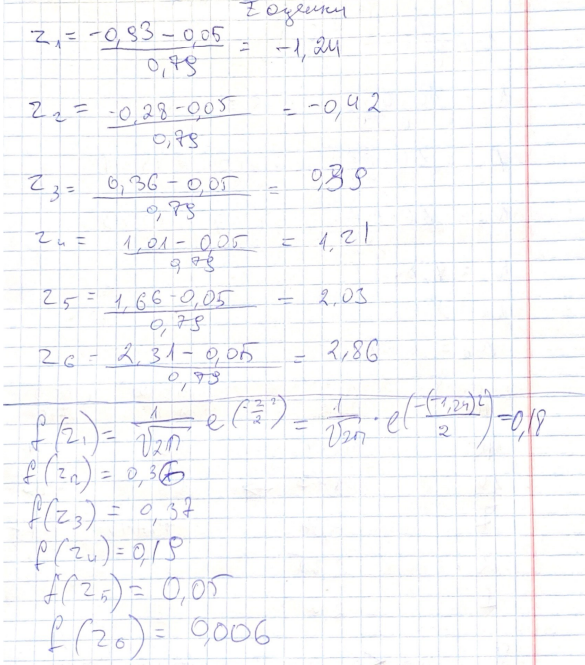
Рисунок 2- Z-оценки и )

Посчитаны теоретические частоты, но так, как есть значения частот <5 , то следует объединить интервалы (Рисунок 3).

Рисунок 3- Теоретические частоты, объединение интервалов

По формуле получено значение и вычислена степень свободы по формуле r = i - k -1. Для нормального распределения k=2 (математическое ожидание и СКО). По таблице критических точек распределения хи-квадрат для r = 1 и уровня значимости =0.05 =3,84 (Рисунок 4).

Рисунок 4- Вычисление

Так как < , то гипотеза о нормальном распределении принимается на заданном уровне значимости.

Выполнена проверка полученных результатов, при помощи функции chi2.ppf в Python для вычисления критического значения критерия хи-квадрат.

Листинг 1- Проверка полученных результатов в Python

import numpy as np

import matplotlib.pyplot as plt

from scipy.stats import chi2

# Данные

x_i = np.array([-0.93, -0.28, 0.36, 1.01, 1.66, 2.31])

n_nabl = np.array([10, 16, 14, 7, 2, 1])

# Количество элементов выборки

N = np.sum(n_nabl)

# Выборочное среднее

m = 0.05

# Выборочное стандартное отклонение (СКО)

sigma = 0.79

# Длина интервала

h = 0.65

z = (x_i - m) / sigma

f_z = (1 / np.sqrt(2 * np.pi)) * np.exp(-0.5 * z**2)

# Теоретические частоты

n_i = N * h / sigma * f_z

# Объединение интервалов с теоретическими частотами меньше 5

new_n_i = []

new_n_nabl = []

current_interval_start = x_i[0]

current_n_i = n_i[0]

current_n_nabl = n_nabl[0]

for i in range(1, len(x_i)):

if current_n_i < 5:

current_interval_start = x_i[i-1]

current_n_i = n_i[i-1]

current_n_nabl = n_nabl[i-1]

if n_i[i] < 5:

current_n_i += n_i[i]

current_n_nabl += n_nabl[i]

else:

new_n_i.append(current_n_i)

new_n_nabl.append(current_n_nabl)

current_interval_start = x_i[i]

current_n_i = n_i[i]

current_n_nabl = n_nabl[i]

new_n_i.append(current_n_i)

new_n_nabl.append(current_n_nabl)

# Преобразование в numpy array

new_n_i = np.array(new_n_i)

new_n_nabl = np.array(new_n_nabl)

# Хи-квадрат наблюдаемое

xi_2_nabl = np.sum((new_n_nabl - new_n_i) ** 2 / new_n_i)

# Количество степеней свободы

r = len(new_n_i) - 2 - 1

# Хи-квадрат критическое

xi_2_krit = chi2.ppf(0.95, r)

if xi_2_nabl < xi_2_krit:

print('Гипотеза о нормальном распределении выборки принимается')

else:

print('Гипотеза о нормальном распределении выборки отвергается')

print('Наблюдаемое значение хи-квадрат:', xi_2_nabl)

print('Критическое значение хи-квадрат:', xi_2_krit)

Рисунок 5- Полученные значения

Проанализировав графики второй выборки и вычисленные метрики было предложено, что выборка имеет равномерное распределение.

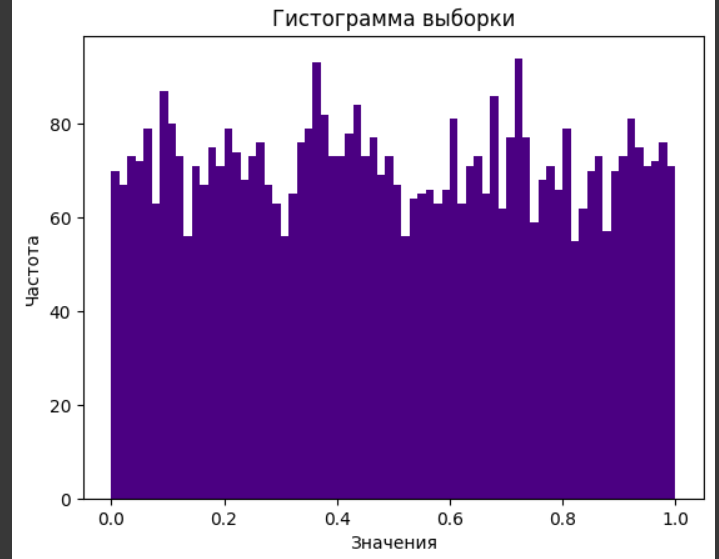
Рисунок 6- Гистограмма второй выборки

Рисунок 7- График эмпирической функции распределения

Для проверки равномерности распределения, воспользуемся критерием согласия Колмогорова-Смирнова.

Можно поэтапно вычислить эмпирическую и теоретическую функции распределения и сравнить максимальное отклонение между ними. И, если это отклонение меньше критического значения критерия, то гипотеза принимается (Рисунок 8).

Листинг 2- Поэтапное вычисление отклонения между эмпирической и теоретической функциями распределения

df = pd.read_csv('myData.csv')

data = df['variant_1'].to_numpy()

data = np.sort(data)

n = len(data)

emp_cdf = np.arange(1, n+1) / (n + 1)

# Вычисление теоретической функции распределения для равномерного закона

a, b = np.min(data), np.max(data)

theo_cdf = uniform.cdf(data, loc=a, scale=b-a)

ks_statistic = np.max(np.abs(emp_cdf - theo_cdf))

print('Ручной расчет K-S статистики:',ks_statistic )

c=1.36/sqrt(n)

print('Критическое значение критерия: ', c)

if ks_statistic > c:

print('Гипотеза о равномерном распределении выборки отвергается')

else:

print('Гипотеза о равномерном распределении выборки принимается')

Рисунок 8- Поэтапный способ расчета

Также, чтобы удостовериться в правильности вычисленного отклонения, можно использовать функцию kstest, которая получает массив с данными и распределение, с которым нужно сравнить выборку (Рисунок 9).

Листинг 2- Поэтапное вычисление отклонения между эмпирической и теоретической функциями распределения

from scipy.stats import kstest, uniform

df = pd.read_csv('myData.csv')

data = df['variant_1'].to_numpy()

data = np.sort(data)

# Применение теста Колмогорова-Смирнова с использованием встроенной функции

ks_statistic, p_value = kstest(data, 'uniform')

print(f'Встроенный расчет K-S статистики: {ks_statistic}')

print(f'p-значение: {p_value}')

alpha = 0.05

if p_value < alpha:

print('Гипотеза о равномерном распределении выборки отвергается')

else:

print('Гипотеза о равномерном распределении выборки принимается')

Рисунок 9- Результаты теста Колмогорова-Смирнова

Расчеты отклонения, полученные ручным способом и с помощью функции совпали. В обоих случаях, результаты показали, что гипотеза о равномерном распределении данных принимается.

Вывод:

В ходе работы была выполнена проверка двух различных гипотез о распределении данных. Для первой проверена гипотеза о нормальном распределении данных с помощью критерия согласия Пирсона, так как < , то гипотеза о нормальном распределении подтвердилась.

Для второй выборки была проверена гипотеза о равномерном распределении данных с помощью критерия согласия Колмогорова-Смирнова. Были проверены два способа расчета максимального отклонения между эмпирической и теоретической функциями распределения. Ручной способ вычисления и с помощью функции kstest показали одинаковые результаты. В результате получилось, что гипотеза о равномерном распределении второй выборки подтвердилась.