Моделирование3

Цель работы: получить навыки моделирования случайных величин с заданным законом распределения методом обратной функции в программной среде MATLAB/GNU Octave, а также первичной оценки качества полученных псевдослучайных чисел.

Вариант 21 (1)

Распределение Рэлея

Ход работы

Формула плотности распределения Рэлея:

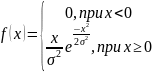
Графики плотности распределения Рэлея для разных значений 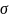показан на рисунке 1.

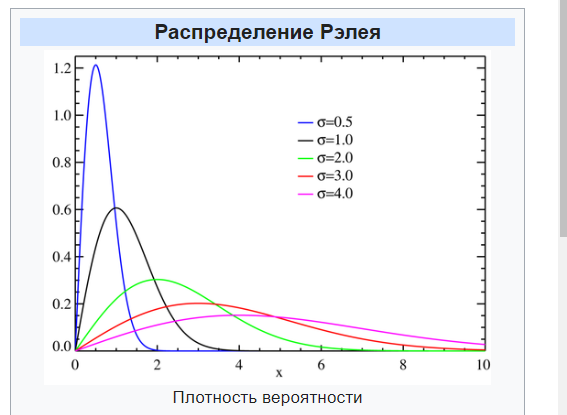
Рисунок 1- Графики плотности распределения Рэлея для значений

Формула функции распределения Рэлея:

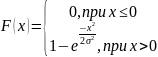
На рисунке 2 представлены графики функции распределения Рэлея для разных значений

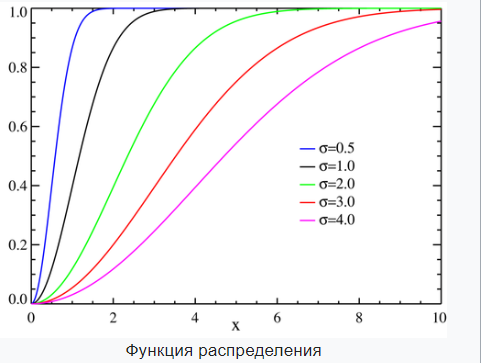
Рисунок 2- Графики функции распределения Рэлея для разных значений

При помощи метода обратной функции выполнено синтезирование алгоритма генерации псевдослучайных чисел с распределением Рэлея.

=

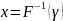
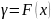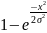
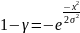
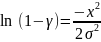
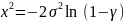
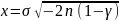
Построены графики функции и плотности распределения Рэлея для значения =1(Рисунок 3-4).

Листинг 1- Построение графика плотности распределения

def fx_raylei(x, sigma=1):

if x >= 0:

return (x / sigma**2) * np.exp(-x**2 / (2 * sigma**2))

else:

return 0

x_values = np.linspace(0, 4)

y_values = np.array([fx_raylei(x) for x in x_values])

plt.plot(x_values, y_values, color='r')

plt.xlabel('x')

plt.ylabel('f(x)')

plt.title('График плотности распределения Рэлея при сигма=1')

plt.legend()

plt.grid(True)

plt.show()

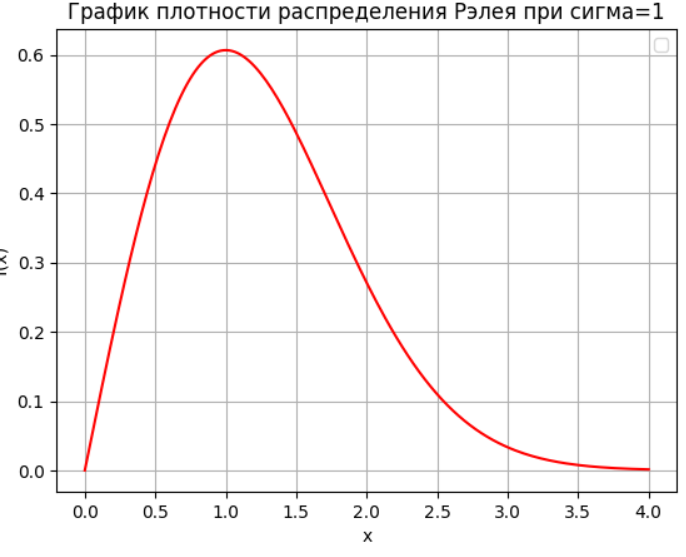
Рисунок 3- График плотности распределения Рэлея

Листинг 2- Построение графика функции распределения Рэлея

def Fx_raylei(x, sigma=1):

if x < 0:

return 0

else:

return 1 - np.exp(-x**2 / (2 * sigma**2))

y_values = np.array([Fx_raylei(x) for x in x_values])

plt.plot(x_values, y_values, color='g')

plt.xlabel('x')

plt.ylabel('F(x)')

plt.title('График функции распределения при сигма =1')

plt.legend()

plt.grid(True)

plt.show()

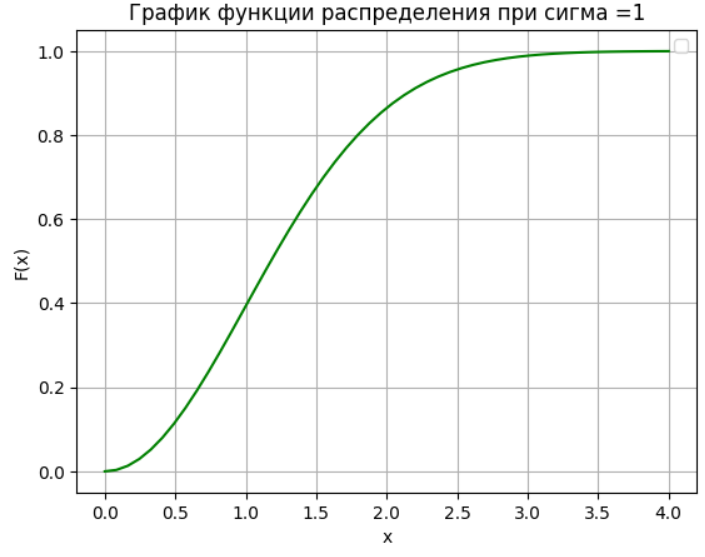
Рисунок 4- График функции распределения Рэлея

Сгенерированы 3 набора псевдослучайных чисел объемом N=100, 5000, 10000.

Построены гистограммы полученной реализации псевдослучайных чисел (Рисунок 5).

Листинг 3- Генерация наборов и построение гистограмм

plt.figure(figsize=(15, 5))

for i, amount in enumerate(amounts):

sigma = 1

random = rayleigh_generator(sigma, amount)

plt.subplot(1, 3, i + 1)

plt.hist(random, bins=30, color=colors[i], alpha=0.7)

plt.title(f'объем {amount} ', fontsize=12)

plt.xlabel('Значение', fontsize=12)

plt.ylabel('Частота', fontsize=12)

plt.grid(True)

plt.suptitle('', fontsize=16)

plt.show()

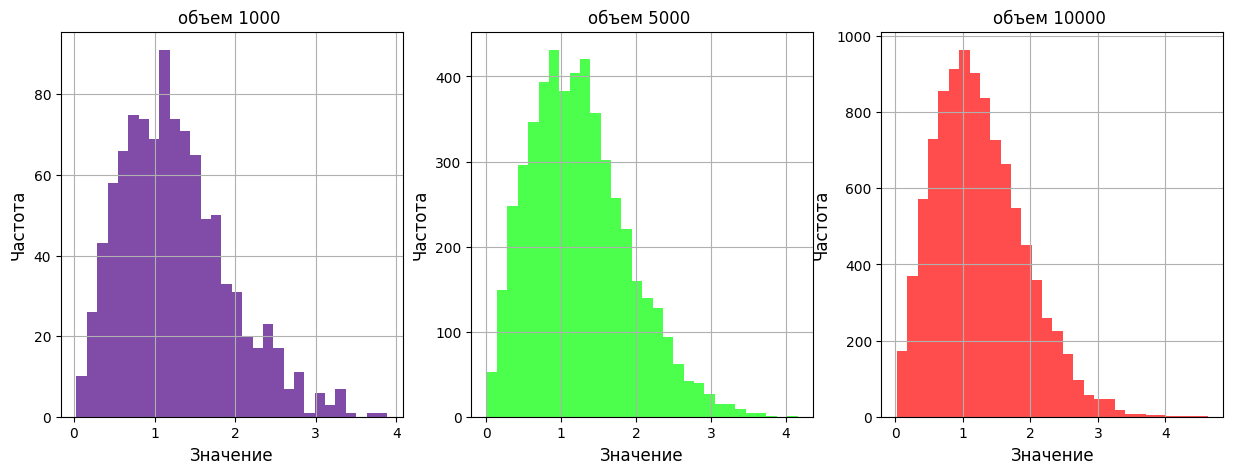
Рисунок 5- Построенные гистограммы для тестирования алгоритма генерации

С увеличением объема выборки форма гистограмм все более приближается к теоретической плотности вероятности распределения Рэлея.

Далее реализованы графики эмпирической функции распределения для различных выборок (Рисунок 6). ЭФР показывает долю наблюдений в выборке, которые меньше или равны определенному значению.

Листинг 4- Реализация графиков эмпирической функции

plt.figure(figsize=(15, 5))

for i, amount in enumerate(amounts):

sigma = 1

random = np.random.rayleigh(sigma, amount)

sorted_random = np.sort(random)

ecdf = np.array([np.sum(sorted_random <= x) / amount for x in sorted_random])

plt.subplot(1, len(amounts), i + 1)

plt.plot(sorted_random, ecdf, colors[i])

plt.title(f'объем {amount}', fontsize=12)

plt.xlabel('Значения', fontsize=13)

plt.ylabel('ECDF', fontsize=13)

plt.grid(True)

plt.tight_layout()

plt.show()

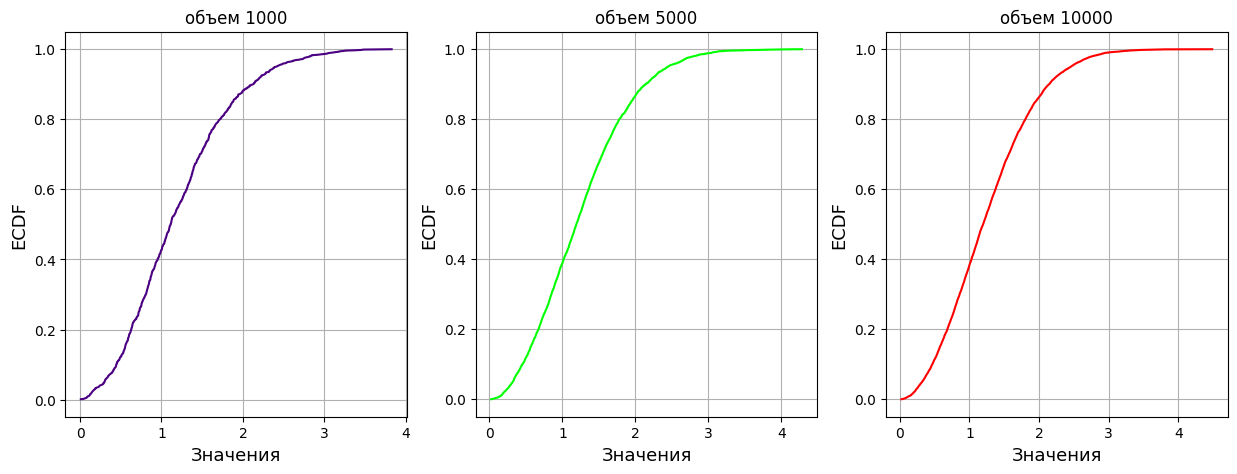
Рисунок 6- Графики эмпирической функции

Графики эмпирической функции всех генераторов показывают, что с ростом объема данных распределение становится более равномерным.

Построены графики распределения на плоскости для разных генераторов и разных объемов выборки. Первые два числа сгенерированного набора являются координатами первой случайной точки, вторые два числа – координатами второй случайной точки и так для всех точек (Рисунок 7).

Листинг 5- Построение графика распределения на плоскости

plt.figure(figsize=(15, 5))

for i, amount in enumerate(amounts):

sigma = 1

random = rayleigh_generator(sigma, amount)

x=[]

y=[]

for k in range(0, len(random), 2):

x.append(random[k])

y.append(random[k + 1])

plt.subplot(1, len(amounts), i + 1)

plt.scatter(x, y, s=3, c=colors[i], label=f'{amount}')

plt.title(f'объем {amount}', fontsize=12)

plt.xlabel('x', fontsize=13)

plt.ylabel('y', fontsize=13)

plt.grid(True)

plt.show()

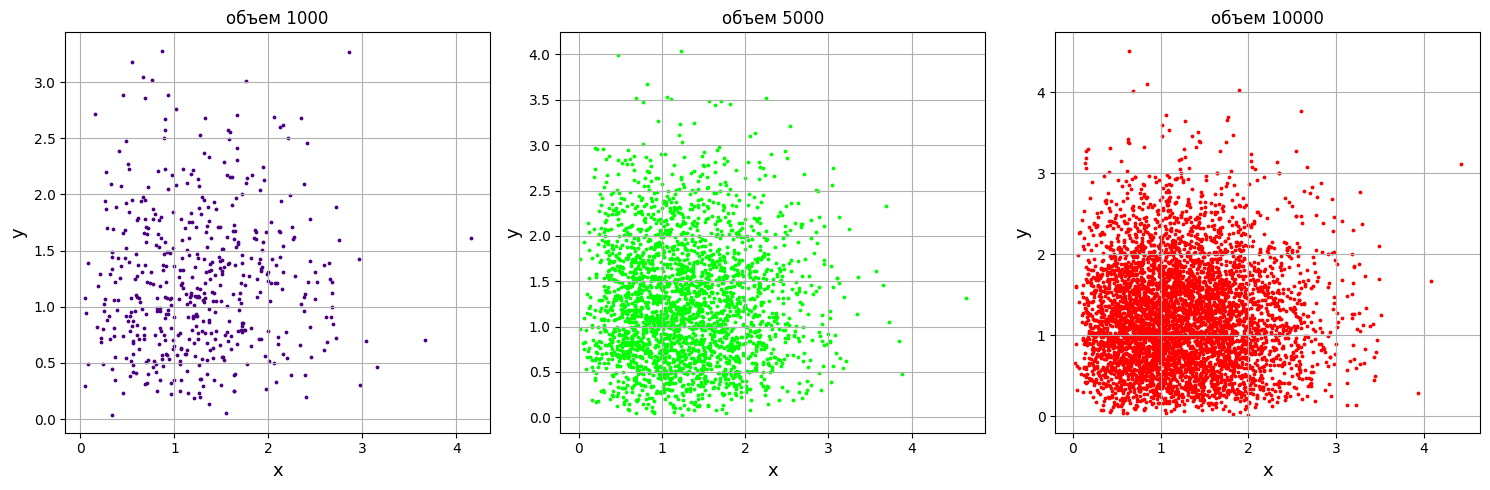
Рисунок 7-Графики распределения на плоскости

С увеличением размера выборки видно, что распределение становится плотнее. Не наблюдается явной корреляции между переменными x и y на любом из графиков.

Вычислены оценки математического ожидания, дисперсии и среднеквадратического отклонения для каждого генератора и каждой выборки.

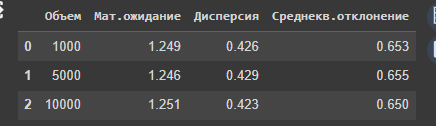
Рисунок 9- Вывод метрик

Если рассчитать по формулам математическое ожидание, дисперсию и среднеквадратическое отклонение со значением :

,

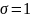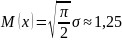
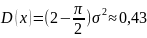
Видно, что теоретические оценки близки вычисленным для разных выборок.

Вывод: для функции распределения Рэлея при помощи метода обратной функции синтезирован алгоритм генерации псевдослучайных чисел. По полученному алгоритму сгенерированы 3 набора псевдослучайных чисел объемом N=1000,5000,10000 чисел. Для оценки качества алгоритма построены гистограммы, графики эмпирической функции распределения и распределение на плоскости. Также вычислены оценки математического ожидания, дисперсии и среднеквадратического отклонения.