Моделирование2

ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

старший преподаватель				Е.К. Григорьев
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №2

МОДЕЛИРОВАНИЕ ГЕНЕРАТОРОВ НОРМАЛЬНО РАСПРЕДЕЛЕННЫХ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ

по курсу: МОДЕЛИРОВАНИЕ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4116
				подпись, дата		инициалы, фамилия

Санкт-Петербург 2024

Цель работы: получить навыки моделирования нормально распределенных псевдослучайных чисел в программной среде MATLAB/GNUOctave, а также первичной оценки качества полученных псевдослучайных чисел.

Вариант 21 (1)

m=20, 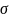=1.

Ход работы

Построен график плотности распределения для нормального закона с параметрами m=20, =1. Для построения использовалась формула плотности вероятности нормального распределения:

,

подставив параметры получается

,

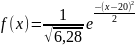Математическое ожидание равно 20, значит вероятность этого значения самая большая.

,

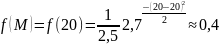
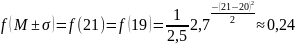
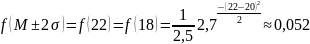
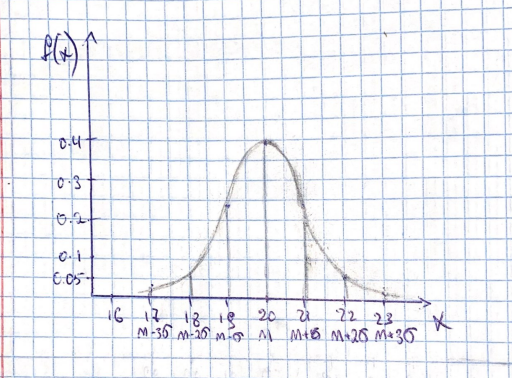
Рисунок 1- График плотности распределения

Для вычисления функции распределения нужно интегрировать функцию плотности вероятности распределения, тогда

= ,

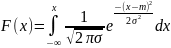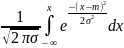так как интеграл такого рода не выражается. Для его нахождения используется функция Лапласа

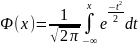
, получается

,

С использованием таблицы значений функции Лапласа и свойства рассчитаны значения функции распределения:

;

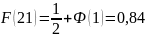
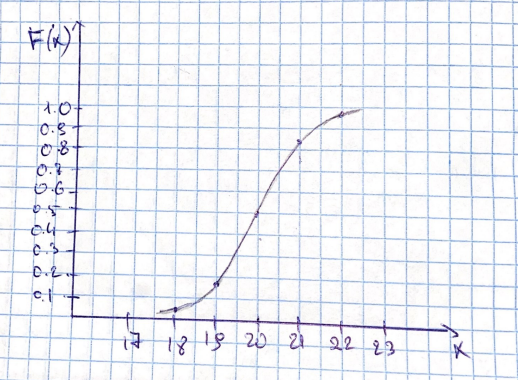
Рисунок 2- График функции распределения

Написан код для построения графика плотности вероятности и функции распределения (Рисунок 3-4)

Листинг 1- Построение графика плотности вероятности

import numpy as np

import matplotlib.pyplot as plt

def pdf(x, m, sigma):

coefficient = 1 / np.sqrt(2 * np.pi * sigma)

exponent = np.exp(-((x - m) ** 2) / (2 * sigma**2))

return coefficient * exponent

m = 20

sigma = 1

x_values = np.linspace(m - 3 * np.sqrt(sigma), m + 3 * np.sqrt(sigma))

pdf_values = pdf(x_values, m, sigma)

plt.plot(x_values, pdf_values)

plt.xlabel('x')

plt.ylabel('f(x)')

plt.title('График плотности распределения распределения')

plt.grid(True)

plt.show()

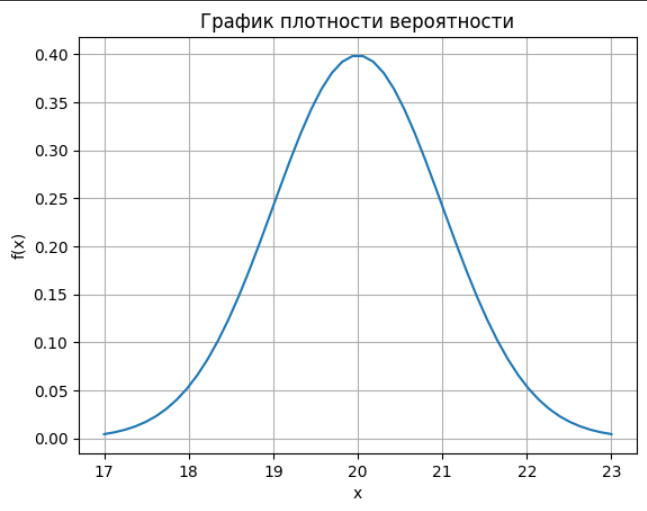
Рисунок 3-График плотности вероятности

Листинг 2- Построение графика функции распределения нормального закона

from scipy import integrate

def standard_normal_pdf(t):

return np.exp(-t**2 / 2)

def laplace_integral(x):

result, _ = integrate.quad(standard_normal_pdf, -np.inf, x)

return (1 / np.sqrt(2 * np.pi)) * result

m = 20

sigma = 1

def function(x, m, sigma):

return 0.5 + 0.5* laplace_integral((x - m) / sigma)

X_values = np.linspace(m - 3 * sigma, m + 3 * sigma, 1000)

F_X_values = [function(x, m, sigma) for x in X_values]

plt.plot(X_values, F_X_values, color='green')

plt.title('График функции распределения')

plt.xlabel('x')

plt.ylabel('F(x)')

plt.grid(True)

plt.show()

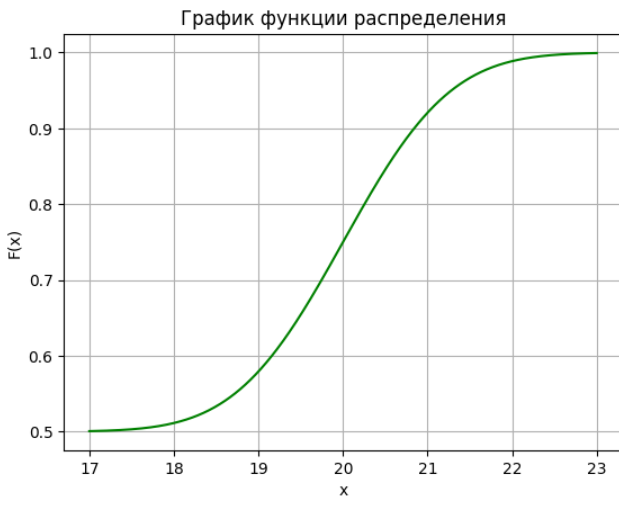
Рисунок 4-График функции распределения

Написана функция генерации псевдослучайных чисел, основанная на предельной центральной теореме. Сумма n одинаково распределенных независимых случайных величин X со средним и дисперсией стремится к нормально распределенной величине с параметрами n , n , при бесконечном увеличении n.

Листинг 3- Функции генерации псевдослучайных чисел, основанная на предельной центральной теореме

def generate_normal_random_numbers(n, m, sigma):

# Генерация n наборов из 12 равномерно распределенных случайных чисел от 0 до 1

uniform_random_numbers = np.random.uniform(low=0.0, high=1.0, size=(n, 12))

# Преобразование суммы равномерно распределенных чисел в нормально распределенные чисвл

normal_random_numbers = m + sigma * (np.sum(uniform_random_numbers, axis=1) - 6)

return normal_random_numbers

Написана функция генерации псевдослучайных чисел с помощью преобразования Бокса-Мюллера (Листинг 4).

Преобразование Бокса-Мюллера позволяет генерировать пару независимых нормально распределённых случайных величин из пары равномерно распределённых случайных величин.

Листинг 4- Преобразование Бокса-Мюллера

def box_muller_transformation(m, sigma, size):

normal_random_numbers = []

for _ in range(size // 2):

# Генерация двух равномерно распределенных случайных чисел

r1, r2 = np.random.uniform(low=0.0, high=1.0, size=2)

# Генерация двух независимых псевдослучайных величин со стандартным нормальным распределением

z0 = np.cos(2 * np.pi * r1) * np.sqrt(-2 * np.log(r2))

z1 = np.sin(2 * np.pi * r1) * np.sqrt(-2 * np.log(r2))

normal_random_numbers.extend([m + sigma * z0, m + sigma * z1])

return np.array(normal_random_numbers)

Реализована генерация псевдослучайных чисел с использованием Полярного метода Марсальи (Листинг 5).

Листинг 5- Полярный метод Марсальи

def marsaglia_polar_method(n, m, sigma):

normal_random_numbers = []

for _ in range(n):

# Генерирация пары равномерно распределенных чисел

x, y = np.random.uniform(-1, 1, size=2)

s = x**2 + y**2

# Отброс s , если s не попадает в [0, 1]

while s >= 1 or s == 0:

x, y = np.random.uniform(-1, 1, size=2)

s = x**2 + y**2

z0 = np.sqrt(-2 * np.log(s) / s) * x

z1 = np.sqrt(-2 * np.log(s) / s) * y

normal_random_numbers.extend([m + sigma * z0, m + sigma * z1])

return np.array(normal_random_numbers)

Также реализована генерация с помощью встроенной функции генерации randn() (Листинг 6).

Листинг 6- Встроенная функция генерации

def function_of_generation(n, m, sigma):

standard_normal_random_numbers = np.random.randn(n)

normal_random_numbers = m + sigma * standard_normal_random_numbers

return normal_random_numbers

Для удобства использования разных алгоритмов генерации нормально распределенных псевдослучайных чисел написана функция generators(), которая принимает имя генератора и объем чисел, который нужно сгенерировать (Листинг 7).

Листинг 7- Функция generators()

def generators(generator, amount):

if generator == 'Генератор, основанный на центр. пред. теореме':

result = generate_normal_random_numbers(amount, m, sigma)

elif generator == 'Генератор с преобр. Бокса-Мюллера':

result = marsaglia_polar_method(amount, m, sigma)

elif generator == 'Полярный метод Марсальи':

result = marsaglia_polar_method(amount, m, sigma)

elif generator == 'Встроенная функция генерации':

result = function_of_generation(amount, m, sigma)

return result

Для тестирования генераторов построены гистограммы, которые показывают, как часто встречаются определённые диапазоны значений среди сгенерированных чисел (Рисунок 5).

Листинг 8- Генерация наборов и построение гистограмм

plt.figure(figsize=(20, 10))

for i, amount in enumerate(amounts):

for j, generator in enumerate(gen_array):

random = generators(generator, amount)

plt.subplot(len(amounts), len(gen_array), i * len(gen_array) + j + 1)

plt.hist(random, bins=30, color=colors[i], alpha=0.7)

plt.title(f'{amount}, {generator}', fontsize=12)

plt.xlabel('Значения', fontsize=12)

plt.ylabel('Частота', fontsize=12)

plt.grid(True)

plt.tight_layout()

plt.show()

Рисунок 5- Построенные гистограммы для тестирования генераторов

Можно сказать, что более крупные выборки приводят к более точному моделированию нормального распределения. Гистограммы полярного метода Марсальи и встроенной функции генерации выглядят самыми симметричными из всех при выборке 1000.

Далее реализованы графики эмпирической функции распределения для различных выборок и различных генераторов (Рисунок 6). ЭФР показывает долю наблюдений в выборке, которые меньше или равны определенному значению.

Листинг 9- Реализация графиков эмпирической функции

graph = None

for i, amount in enumerate(amounts):

for j, generator in enumerate(gen_array):

random = generators(generator, amount)

x = np.sort(random)

ecdf = ECDF(random)

y = ecdf(x)

plt.figure(2, figsize=(24, 16))

current_subplot = plt.subplot(len(amounts), len(gen_array), i * len(gen_array) + j + 1)

plt.plot(x, y, colors[i])

plt.title(f'{amount}, {generator}', fontsize=13)

plt.xlabel('Значения', fontsize=12)

plt.ylabel('ECDF', fontsize=12)

plt.grid(True)

plt.show()

Рисунок 6- Графики эмпирической функции

Графики эмпирической функции становятся более гладкими с увеличением размера выборки. По форме графиков можно судить о хорошем соответствии эмпирических данных теоретическому распределению

Построены графики распределения на плоскости для разных генераторов и разных объемов выборки. Первые два числа сгенерированного набора являются координатами первой случайной точки, вторые два числа – координатами второй случайной точки и так для всех точек (Рисунок 7).

Листинг 10- Построение графика распределения на плоскости

plt.figure(figsize=(24, 15))

for i, amount in enumerate(amounts):

for j, generator in enumerate(gen_array):

random = generators(generator, amount)

x=[]

y=[]

for k in range(0, len(random), 2):

x.append(random[k])

y.append(random[k + 1])

plt.subplot(len(amounts), len(gen_array), i * len(gen_array) + j + 1)

plt.scatter(x, y, s=3, c=colors[i], label=f'{amount}')

plt.title(f'{amount}, {generator}', fontsize=13)

plt.xlabel('x', fontsize=13)

plt.ylabel('y', fontsize=13)

plt.grid(True)

Рисунок 7-Графики распределения на плоскости

На всех графиках точки более плотно сгруппированы в центральной области, что указывает на высокую вероятность встречаемости значений вокруг среднего. С увеличением размера выборки видно, что распределение становится плотнее и более сфокусированным вокруг центра.

Для сравнения распределения сгенерированных данных с нормальным теоретическим распределением реализованы графики «квантиль-квантиль» (Рисунок 8). Если сгенерированные данные имеют нормальное распределение, точки должны располагаться на прямой линии, которая указывает на соответствие теоретическому распределению.

Листинг 11- Построение графика квантиль-квантиль»

# Создание нового графика

fig, axes = plt.subplots(len(amounts), len(gen_array), figsize=(20, 15))

for i, amount in enumerate(amounts):

for j, generator in enumerate(gen_array):

# Генерация случайных данных

random = generators(generator, amount)

# Построение QQ-plot

sm.qqplot(random, ax=axes[i, j], line='s', label=f'{amount}, {generator}', alpha=0.5)

axes[i, j].set_title(f'{amount}, {generator}', fontsize=12)

axes[i, j].set_xlabel('Теоретические квантили', fontsize=12)

axes[i, j].set_ylabel('Квантили исследуемой выборки', fontsize=12)

axes[i, j].grid(True)

# Регулировка расположения графиков

plt.tight_layout()

plt.show()

Рисунок 8- Графики «квантиль-квантиль»

Сгенерированные данные соответствуют нормальному распределению, так как на всех графиках большинство точек располагаются на прямой линии.

Вычислены оценки математического ожидания, дисперсии и среднеквадратического отклонения для каждого генератора и каждой выборки.

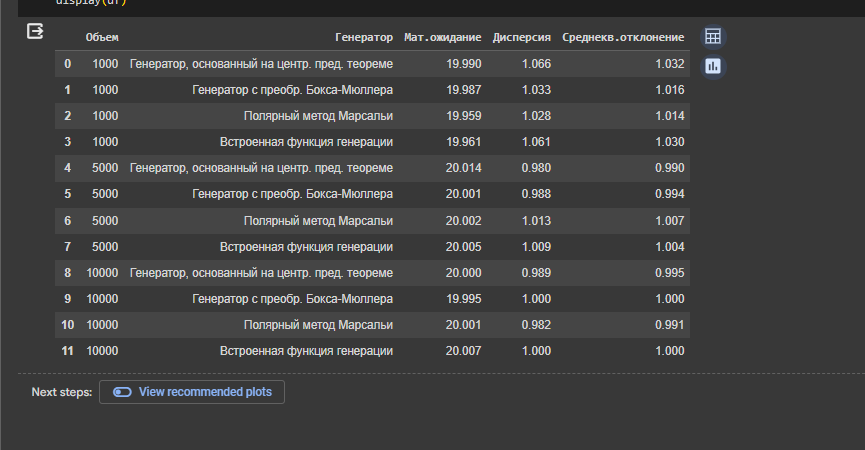
Рисунок 9- Вывод метрик

Математическое ожидание близко к 20 для всех методов.

Дисперсия и среднеквадратичное отклонение различаются среди методов, но остаются в пределах близких к 1. Это показывает, что разброс генерируемых чисел относительно среднего значения для всех методов примерно одинаков.

С увеличением объема выборки математическое ожидание и среднеквадратичное отклонение становятся стабильнее,

Вывод: написаны функции реализации генератора, основанного на центральной предельной теорем, генератора с преобразованием Бокса-Мюллера, полярного метода Марсальи и генератора с использованием встроенной функции генерации. Произведена генерация нормально распределенных псевдослучайных чисел с использованием разных генераторов и разного объема данных. Для тестирования генераторов построены гистограммы, графики эмпирической функции распределения, графики распределения на плоскости и графики «квантиль-квантиль». Также вычислены метрики для оценки качества генераторов.