
Моделирование1
.docxЦель работы: получить навыки моделирования наиболее известных генераторов равномерно распределенных псевдослучайных чисел в программной среде MATLAB/GNU Octave, а также первичной оценки качества полученных псевдослучайных чисел.
Ход работы
Для генерации наборов псевдослучайных чисел разными алгоритмами с разным объемом чисел, написаны функции реализации мультипликативного конгруэнтного генератора (Листинг 1), генератора Фибоначчи с запаздыванием (Листинг 2), алгоритма Вихря Мирсенна (Листинг 3).
Формула, используемая для реализации мультипликативного конгруэнтного генератора
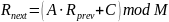 ,
где
,
где
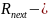 следующее
псевдослучайное число в последовательности,
следующее
псевдослучайное число в последовательности,
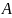 -
мультипликатор,
-
мультипликатор,
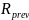 -
предыдущее псевдослучайное число в
последовательности,
-
предыдущее псевдослучайное число в
последовательности,
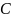 -инкремент,
-инкремент,
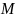 -
модуль.
-
модуль.
Процесс
генерации состоит в последовательном
вычислении
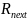 на основе предыдущего значения
начиная с
на основе предыдущего значения
начиная с
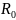 .
Каждое новое значение нормализуется
делением на
для получения числа в диапазоне от 0 до
1.
.
Каждое новое значение нормализуется
делением на
для получения числа в диапазоне от 0 до
1.
Листинг 1. Реализация мультипликативного конгруэнтного генератора
def multiplicative_congruential_generator(N):
# Параметры генератора
A = 7**5
C = 0
M = 2**32 - 1
# Начальное значение
R0 = 2**(-52)
# Инициализация массива для хранения псевдослучайных чисел
random_numbers = []
R_prev = R0
# Генерация последовательности
for i in range(N):
R_next = (A * R_prev + C) % M
random_numbers.append(R_next / M)
R_prev = R_next
return random_numbers
Для реализации генератора Фибоначчи с запаздыванием использовалась формула:
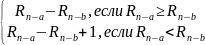 ,
где
,
где
n — индекс текущего генерируемого числа в последовательности,
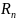 -
n-е сгенерированное псевдослучайное
число,
-
n-е сгенерированное псевдослучайное
число,
a и b — параметры запаздывания, представляющие собой индексы предыдущих значений в последовательности, используемых для генерации нового значения,
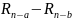 -
значения последовательности, отстающие
от текущего на a и b позиций.
-
значения последовательности, отстающие
от текущего на a и b позиций.
Создается массив чисел заданной длины, начальные значения которого заполняются нулями. Генерируются случайные значения и помещаются в начало массива, в количестве, равном максимуму между a и b. Затем выполняется обход всех остальных элементов, для каждого нового числа в массиве вычисляется его значение как разность между двумя предыдущими числами массива, отстающими на заданные расстояния a и b. Если полученная разность отрицательна, к результату добавляется 1, чтобы гарантировать неотрицательное значение.
Листинг 2. Реализация генератора Фибоначчи с запаздыванием
def lagged_fibonacci_generator(N, a, b):
R = np.zeros(N)
R[:max(a, b)] = np.random.rand(max(a, b))
for n in range(max(a, b), N):
if R[n-a] >= R[n-b]:
R[n] = R[n-a] - R[n-b]
else:
R[n] = R[n-a] - R[n-b] + 1
return R
Генератор вихря Мерсенна является выбором по умолчанию для генерации псевдослучайных чисел во многих программных средах, для его реализации используется метод random.rand библиотеки numpy (Листинг 3).
Листинг 3- Реализация генератора Вихря Мерсенна
def mersenne_generator(N):
# Инициализация генератора вихря Мерсенна
s = np.random.RandomState(seed=None)
# Генерация псевдослучайных чисел
random_numbers = s.rand(N)
return random_numbers
Для удобства использования разных алгоритмов генерации псевдослучайных чисел, написана функция generators(), которая принимает имя генератора и объем чисел, который нужно сгенерировать (Листинг 4).
Листинг 4- Функция generators()
def generators(generator, amount):
if generator == 'Мультипликативный конгруэнтный':
result = multiplicative_congruential_generator(amount)
elif generator == 'Фиббоначчи с запаздыванием':
result = lagged_fibonacci_generator(amount, 63, 31)
elif generator == 'Вихрь Мерсенна':
result = mersenne_generator(amount)
return result
Далее происходит генерация псевдослучайных чисел с использованием разных генераторов и разных объемов данных (Рисунок 1). Для тестирования генераторов построены гистограммы, которые показывают, как часто встречаются определённые диапазоны значений среди сгенерированных чисел.
Листинг 4- Генерация наборов и построение гистограмм
amounts = [1000, 5000, 10000]
colors = ['Indigo', 'lime', 'red']
gen_array = ['Мультипликативный конгруэнтный', 'Фиббоначчи с запаздыванием', 'Вихрь Мерсенна']
np.random.seed(100)
for i, amount in enumerate(amounts):
for generator in gen_array:
random = generators(generator, amount)
# Построение гистограммы
plt.figure(1, figsize=(15, 15))
plt.subplot(3, 3, i * 3 + gen_array.index(generator) + 1)
plt.hist(random, bins=50, color=colors[i], alpha=0.7)
plt.title(f'{amount}, {generator}', fontsize=12)
plt.xlabel('Значения', fontsize=12)
plt.ylabel('Частота', fontsize=12)
plt.grid(True)
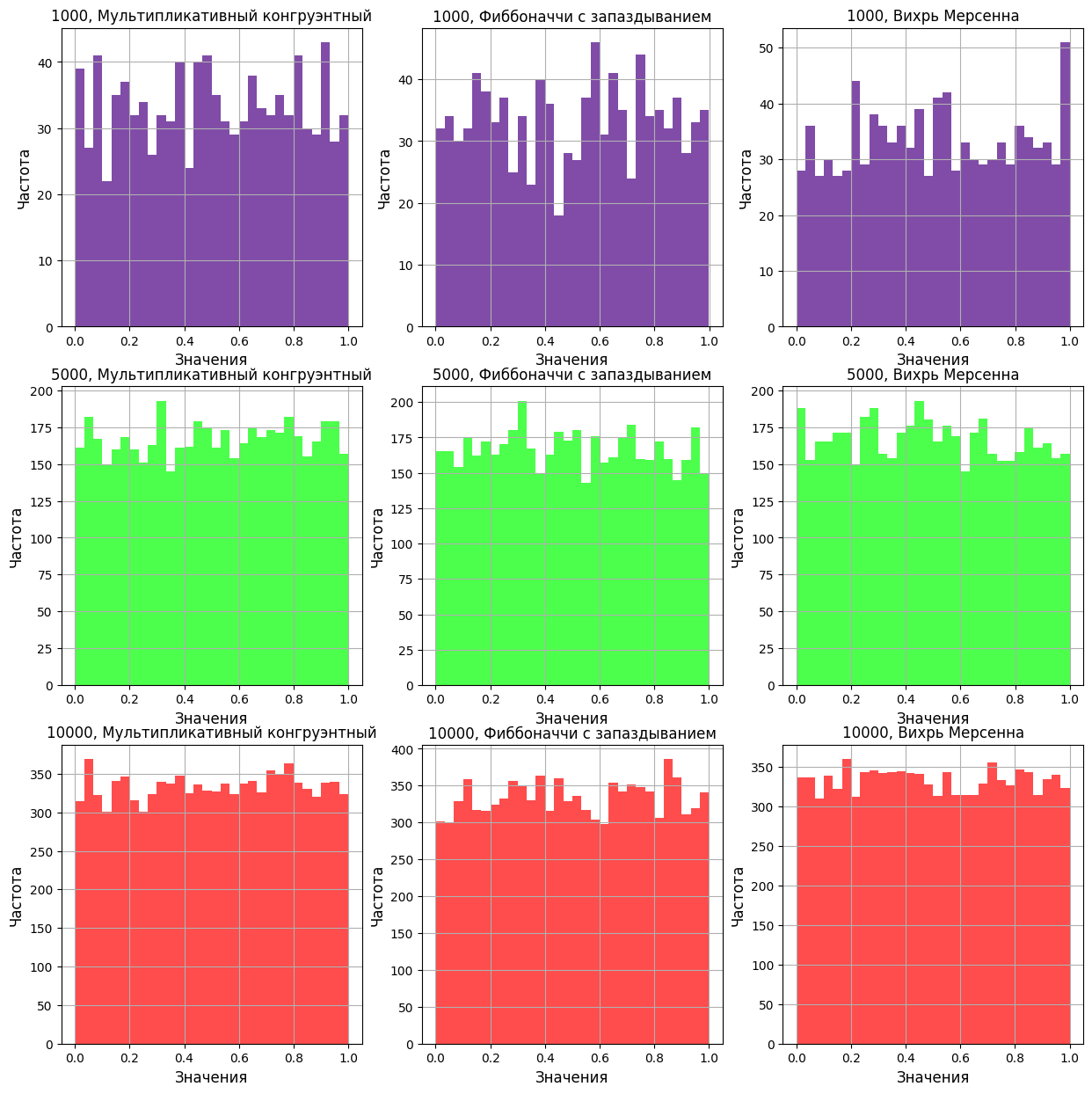
Рисунок 1- Построенные гистограммы для тестирования генераторов
На гистограммах для выборок 5000 и 10000 чисел видно, что распределение становится плотнее и более равномерным, значит с увеличением размера выборки улучшается равномерность распределения. Из трех генераторов, Вихрь Мерсенна показывает самое равномерное распределение.
Далее реализованы графики эмпирической функции распределения для различных выборок и различных генераторов (Рисунок 2). ЭФР показывает долю наблюдений в выборке, которые меньше или равны определенному значению.
Создается массив сортированных сгенерированных случайных чисел, значения используются в качестве точек для построения ECDF. На основе массива случайных чисел создается объект ECDF, который представляет собой эмпирическую функцию для данных.
Значения ECDF вычисляются для каждой точки из ранее созданного массива, используя созданный объект ECDF. На горизонтальной оси отложены значения случайных величин. На вертикальной оси отложены доли наблюдений, не превышающих соответствующие значения на горизонтальной оси. Также реализован более приближенный график эмпирической функции для генератора Фиббоначи с запаздыванием при выборке 1000.
Листинг 5- Реализация графиков эмпирической функции
graph = None
for i, amount in enumerate(amounts):
for j, generator in enumerate(gen_array):
random = generators(generator, amount)
x = np.sort(random)
# Вычисление ECDF для сгенерированных случайных чисел
ecdf = ECDF(random)
y = ecdf(x)
plt.figure(2, figsize=(15, 15))
current_subplot = plt.subplot(3, 3, i * 3 + j + 1)
plt.plot(x, y, colors[i])
plt.title(f'{amount}, {generator}', fontsize=13)
plt.xlabel('Значения', fontsize=13)
plt.ylabel('ECDF', fontsize=13)
plt.grid(True)
if amount == 1000 and j == 1:
graph = (x, y)
if graph is not None:
plt.figure(figsize=(50, 50))
x, y = graph
plt.step(x, y, where='post', color='indigo', linewidth=2.5)
plt.title('Приближенный график для генератора Фиббоначи с запаздыванием для выборки 1000', fontsize=13)
plt.xlabel('Значения', fontsize=13)
plt.ylabel('ECDF', fontsize=13)
plt.grid(True)
plt.show()
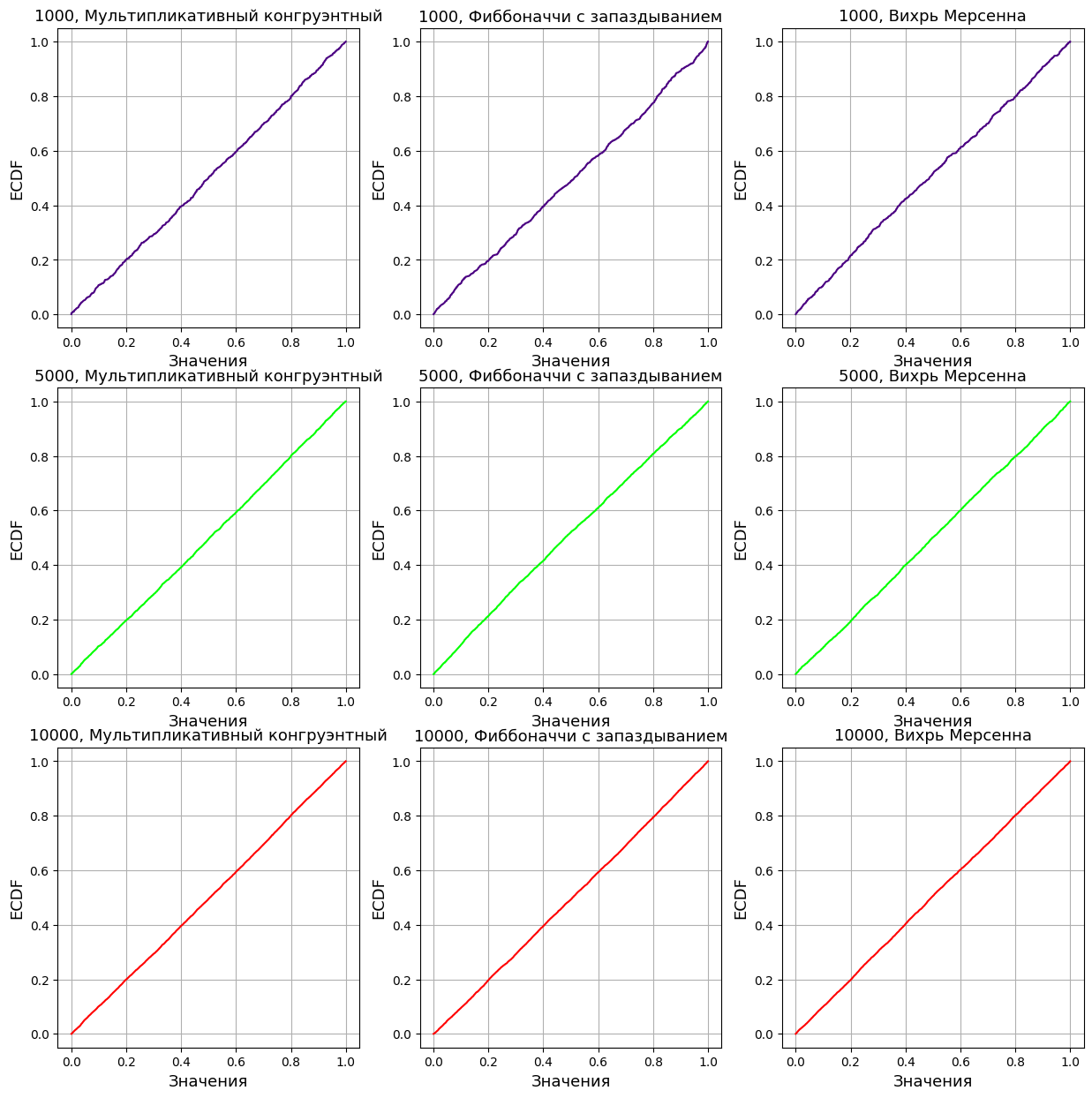
Рисунок 2- Графики эмпирической функции
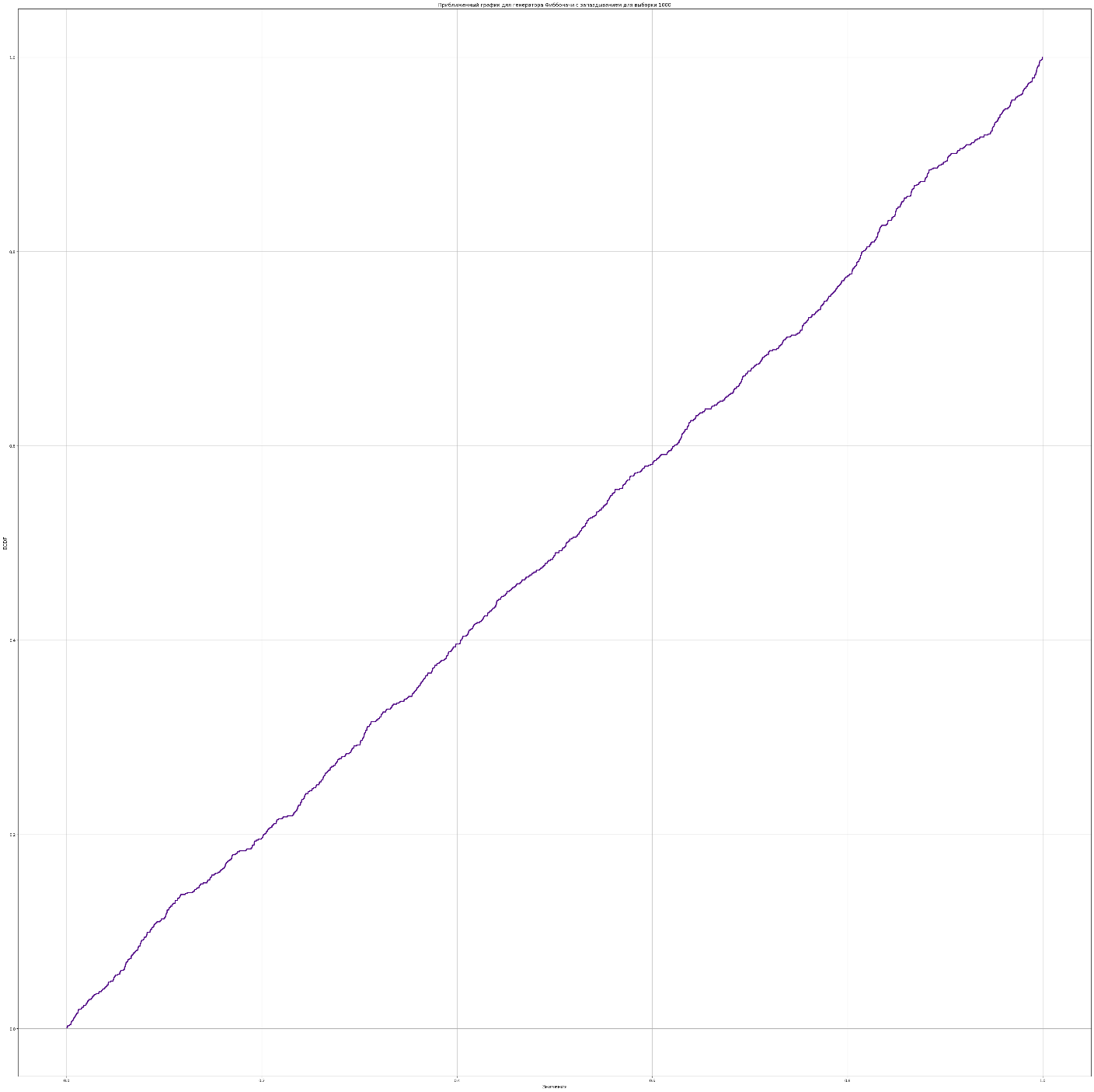
Рисунок 3- Приближенный график эмпирической функции
Графики эмпирической функции всех генераторов показывают, что с ростом объема данных распределение становится более равномерным. Все три алгоритма кажутся эффективными в генерации чисел с равномерным распределением, особенно при больших размерах выборки. Линейность графиков показывает равномерность распределения. Генератор фиббоначи с запаздыванием имеет более кривую линию при объеме 1000 чисел, возможно, что для более равномерного распределения генератору требует больший размер выборки.
Построены графики распределения на плоскости для разных генераторов и разных объемов выборки. Первые два числа сгенерированного набора являются координатами первой случайной точки, вторые два числа – координатами второй случайной точки и так для всех точек. (Рисунок 4).
Листинг 6- Построение графика распределения на плоскости
plt.figure(figsize=(15, 15))
for i, amount in enumerate(amounts):
for j, generator in enumerate(gen_array):
random = generators(generator, amount)
x=[]
y=[]
for k in range(0, len(random), 2):
x.append(random[k])
y.append(random[k + 1])
plt.subplot(3, 3, i * 3 + j + 1)
plt.scatter(x, y, s=3, c=colors[i], label=f'{amount}')
plt.title(f'{amount}, {generator}', fontsize=13)
plt.xlabel('x', fontsize=13)
plt.ylabel('y', fontsize=13)
plt.grid(True)
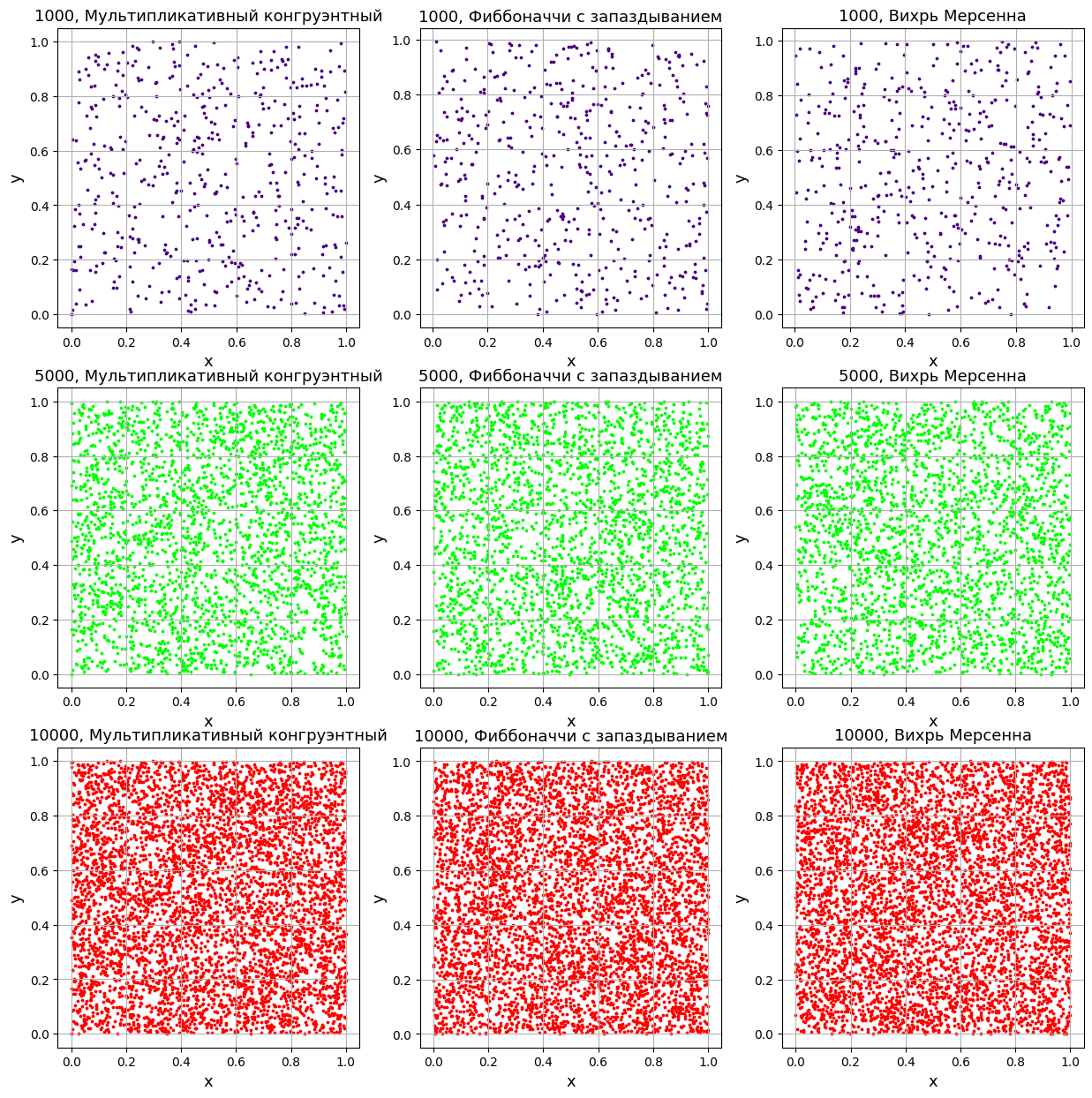
Рисунок 4-График распределения на плоскости
Точки на всех трех графиках равномерно распределены по пространству графика, что свидетельствует о том, что генерируемые значения хорошо распределены, особенно при увеличении размера выборки.
Вычислены оценки математического ожидания, дисперсии и среднеквадратического отклонения для каждой выборки (Рисунок 5).
Листинг 7- Подсчет метрик
records = []
for i, amount in enumerate(amounts):
for generator in gen_array:
random =generators(generator, amount)
mean_val = np.mean(random).round(3)
var_val = np.var(random).round(3)
std_val = np.std(random).round(3)
record = {
'Объем': amount,
'Генератор': generator,
'Мат.ожидание': mean_val,
'Дисперсия': var_val,
'Среднекв.отклонение':std_val
}
records.append(record)
df = pd.DataFrame(records)
display(df)
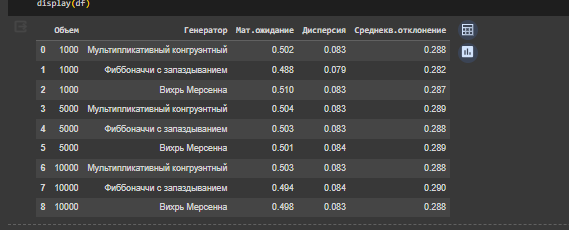
Рисунок 5-Вывод метрик
Мультипликативный конгруэнтный генератор и Вихрь Мерсенна показывают математическое ожидание близкое к 0.5, что является хорошим показателем, однако, для выборок 5000 и 10000 Вихрь Мерсенна показывает самое лучшее математическое ожидание.
Математическое ожидание для "Фибоначчи с запаздыванием" немного ниже при объеме выборки 1000, что может указывать на менее равномерное распределение по сравнению с остальными генераторами. Дисперсия у Фибоначчи с запаздыванием также ниже при том же объеме выборки, что может свидетельствовать о меньшем разбросе чисел вокруг среднего.
Можно сказать, что все генераторы хорошо поддерживают равномерное распределение случайных чисел, но генератор "Фибоначчи с запаздыванием" может требовать большей выборки для достижения такой же равномерности, как другие генераторы.
Посчитаны теоретические значения математического ожидания, дисперсии и среднеквадратического отклонения для равномерного распределения с параметрами (0,1), и построены графики плотности распределения f(x) и функции распределения F(x) равномерного закона распределения (Рисунок 6).
Листинг 8- Подсчет метрик и вывод графиков
import numpy as np
import matplotlib.pyplot as plt
a = 0
b = 1
M = (a + b) / 2
D = ((b - a) ** 2) / 12
O = np.sqrt(D)
def f(x):
return np.where((x >= a) & (x <= b), 1 / (b - a), 0)
def F(x):
return np.where(x < a, 0, np.where(x < b, (x - a) / (b - a), 1))
x_values = np.linspace(-0.1, 1.1, 1000)
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.plot(x_values, f(x_values), label='f(x)', color='red')
plt.title('Плотность равномерного распределения f(x)')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid(True)
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(x_values, F(x_values), label='F(x)', color='green')
plt.title('Функция распределения F(x)')
plt.xlabel('x')
plt.ylabel('F(x)')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
print('математическое ожидание :',M)
print('Дисперсия: ', D)
print('Среднеквадратическое отклонение: ', O)
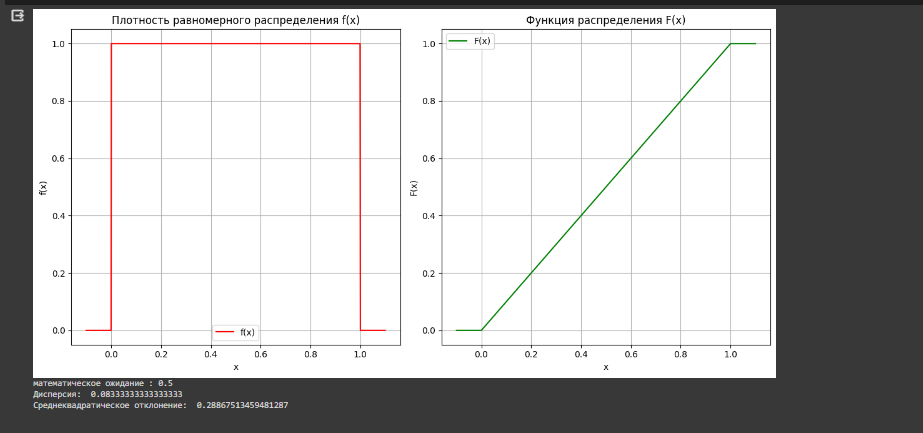
Рисунок 6- Графики плотности и функции распределения
Это график плотности равномерного распределения f(x) показывает, что вероятность каждого события в интервале [0,1] постоянна и равна 1. Плотность вне этого интервала равна 0.
График функции распределения F(x) равномерного распределения показывает, какова вероятность того, что случайно выбранное значение будет меньше или равно определённому значению x.
Вывод: написаны функции реализации мультипликативного конгруэнтного генератора, генератора Фибоначчи с, алгоритма Вихря Мирсенна. Произведена генерация псевдослучайных чисел с использованием разных генераторов и разным объемом данных. Для тестирования генераторов построены гистограммы, графики эмпирической функции распределения и графики распределения на плоскости. Также вычислены метрики для оценки качества генераторов.
