ГУАП

КАФЕДРА № 82

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доцент, канд. техн. наук				А.Д. Державина
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №4

ИНТЕЛЛЕКТУАЛЬНЫЙ АНАЛИЗ ДАННЫХ. МЕТОД РЕГРЕССИИ

по курсу: ИНТЕЛЛЕКТУАЛЬНЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	4116
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2024

Цель работы: изучить пример предложенного разработчиками RM по использованию модели метода деревьев решений для анализа данных. Построить модель дерева решений для своего набора данных.

Цель работы: изучить метод линейной регрессии к заданному набору данных.

Ход работы

Запущена модель линейной регрессии, подготовленная разработчиками пакета RM, которая позволяет делать численные прогнозы для загруженного набора данных (Рисунок 1-3)

Рисунок 1 - Выбор модели линейной регрессии

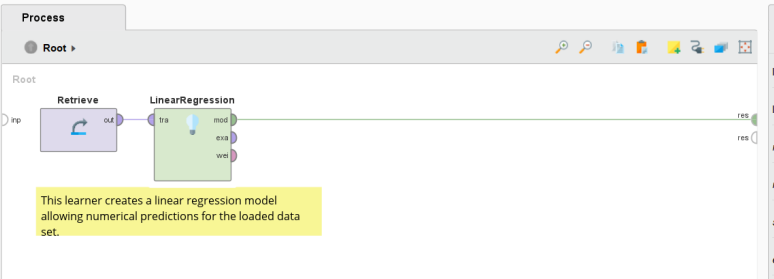
Рисунок 2 – Модель линейной регрессии

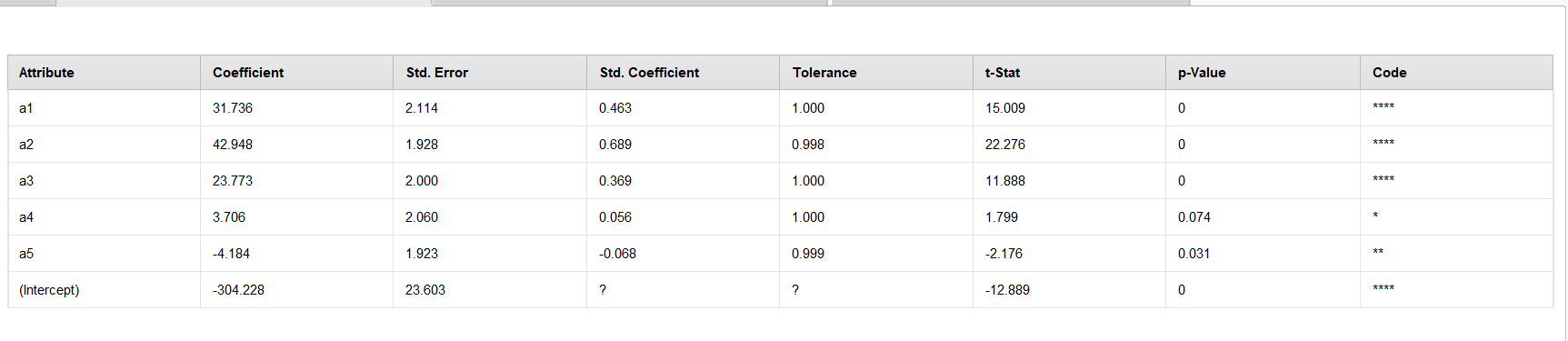
Рисунок 3 – Результат моделирования

Рисунок 4 – Описание линейной регрессии

По результату моделирования можно сказать, что наибольший вклад в модель оказывают переменные a1 и a2. С увеличением значений этих переменных предсказанная целевая переменная будет увеличиваться значительно. Переменная a5 имеет отрицательный коэффициент, что указывает на обратную зависимость.

Если значение p-value меньше 0.05, значит коэффициент статистически значим. В данном случае a1, a2, a3 имеют p-value равное 0, что говорит о их сильной статистической значимости. Переменная a4 имеет p-value выше порогового значения 0.05, значит, её вклад в модель не является статистически значимым.

Импортирован набор данных с характеристиками бриллиантов и ценами на них. Реализован процесс создания модели полиномиальной регрессии, данные разделены на части 0.8 и 0.2 (Рисунок 5-9).

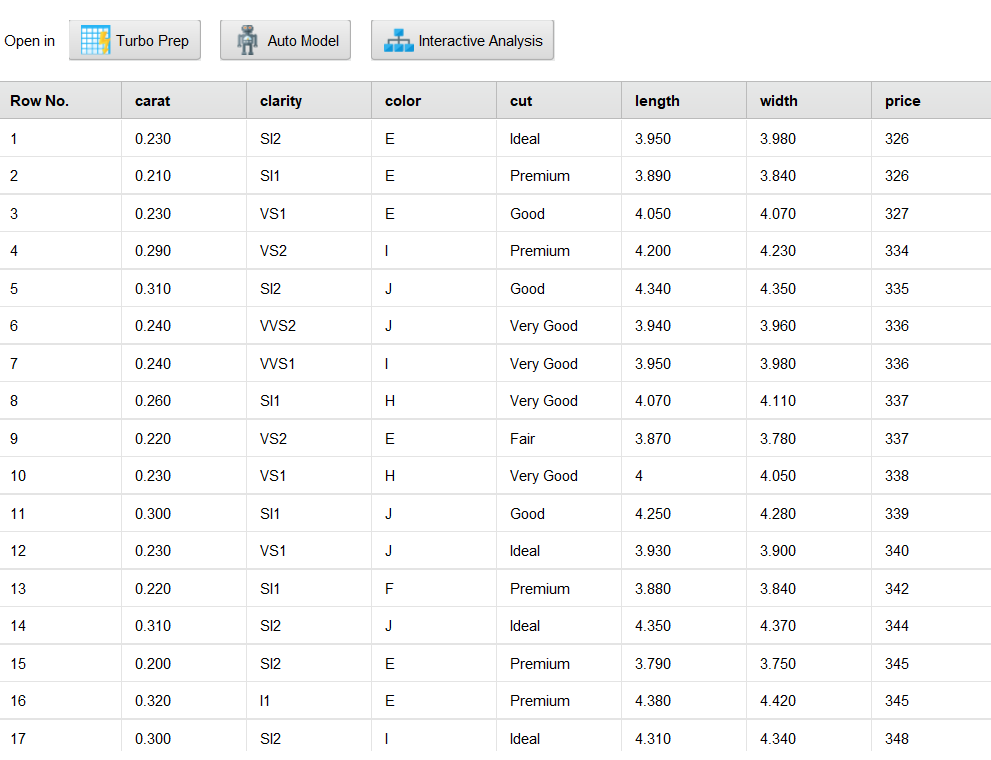
Рисунок 5– Исходный набор данных

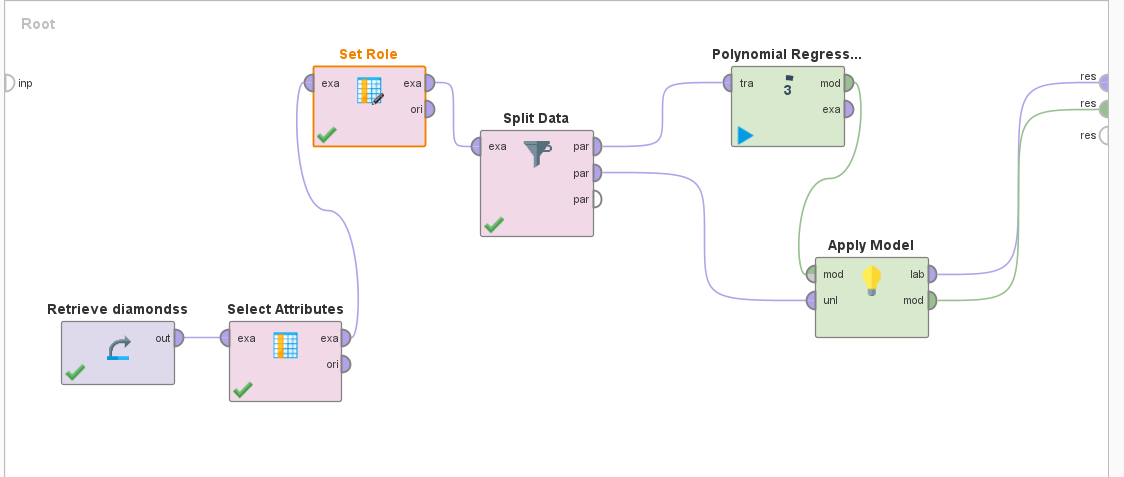
Рисунок 6 – Процесс моделирования

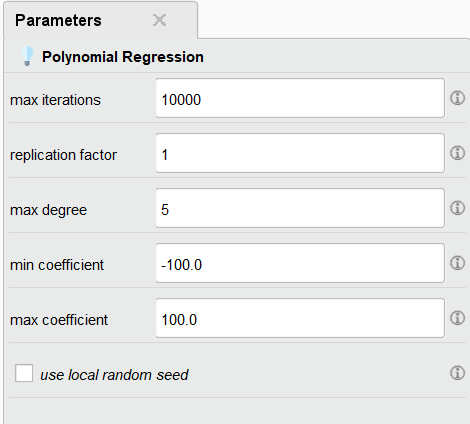
Рисунок 7 – Параметры модели

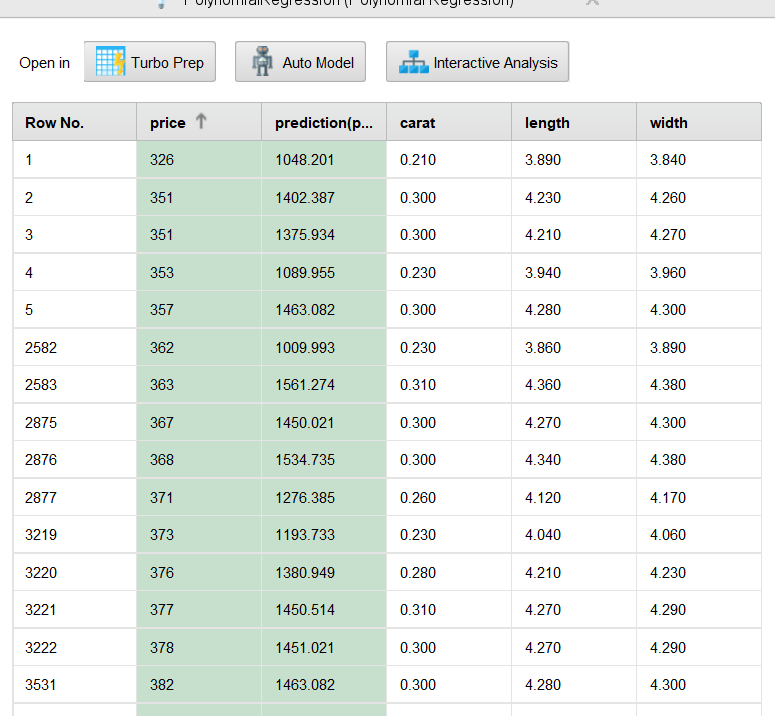
Рисунок 8 – Результат предсказания

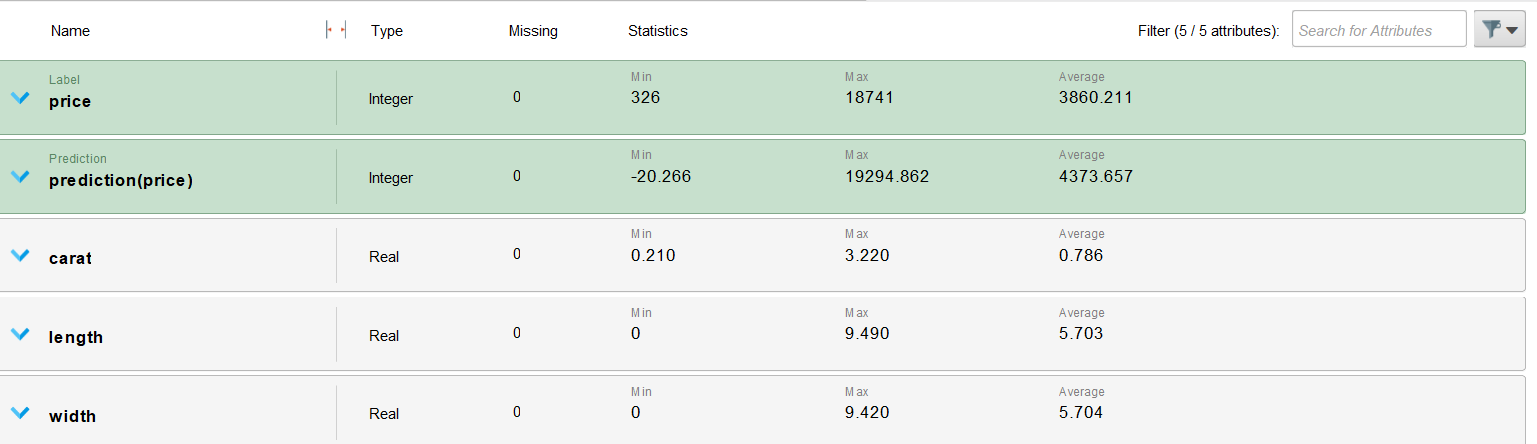
Рисунок 9 – Статистика

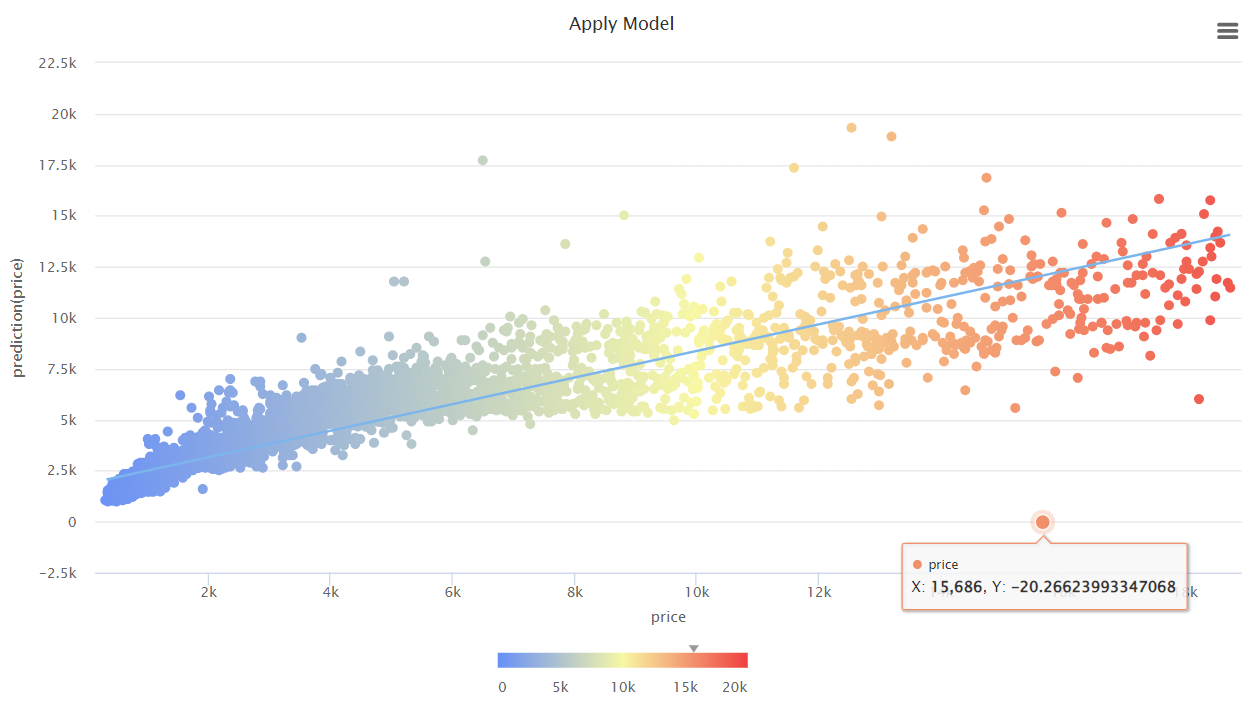
Рисунок 10– Визуализация истинных и предсказанных значений

Предсказанные значения близки к истинным, наблюдается выброс при истинном значении 15686 модель предсказала -20.26.

Вывод: изучены модели линейной и полиномиальной регрессий. Для собственного набора данных применен метод полиномиальной регрессии.

Ответы на контрольные вопросы:

1. Как переводится с латинского слово «регрессия»?

regressus — возвращение, обратное движение

2. Что такое регрессия? 

Регрессия — это статистический метод, который связывает зависимую переменную с одной или несколькими независимыми переменными .

3. Линия регрессии - это

Линия регрессии определяется как прямая линия, которая представляет связь между зависимой переменной (Y) и независимой переменной (X) в уравнении линейной регрессии

4. Гипотеза линейной регрессии - предположение о линейной зависимости между независимыми переменными X и зависимой переменной Y