
Доп.задание
..pdf
Задание: взвесить шестиугольную решетку и написать для нее поиск кратчайшего пути в глубину, учитывая вес ребер.
Листинг 1. Взвешенная шестиугольная решетка
import numpy as np import networkx as nx
import matplotlib.pyplot as plt
def create_hexagonal_grid(M): if M < 2:
return np.array([])
# Создание пустой матрицы смежности размером M x M matrix_size = M * M
matrix = np.zeros((matrix_size, matrix_size), dtype=int)
# Заполнение матрицы смежности for v in range(matrix_size):
R = v // M # Вычисление номера строки
C = v % M # Вычисление номера столбца
#Условия для соединения вершин шестиугольной решетки
if (R % 4 == 0 and C % 2 == 1) or (R % 4 == 2 and C % 2 == 0): if R > 0:
matrix[v][v - M] = matrix[v - M][v] = np.random.randint(1, 10)#
Соединяем с вершиной выше
if R < (M - 1) and C < (M - 1):
matrix[v][v + M + 1] = matrix[v + M + 1][v] = np.random.randint(1, 10) # Соединяем с вершиной справа ниже
if R < (M - 1) and C > 0:
matrix[v][v + M - 1] = matrix[v + M - 1][v] = 1 # Соединяем с вершиной слева ниже
non_isolated = np.array([i for i in range(matrix_size) if np.sum(matrix[i]) > 1], dtype=int)
matrix = matrix[non_isolated][:, non_isolated]
return matrix
M = 6 # Размер решетки M на M matrix = create_hexagonal_grid(M)
print("Матрица смежности созданной решетки после удаления изолированных вершин:")
print(matrix)
G = nx.from_numpy_array(matrix)
pos = nx.spring_layout(G, iterations=150000, seed=1000)
# Создаём словарь с весами рёбер
edge_labels = nx.get_edge_attributes(G, 'weight')
nx.draw(G, pos, with_labels=True, node_size=500, node_color="skyblue", font_size=10, font_weight="bold")
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels) # Отображение весов рёбер
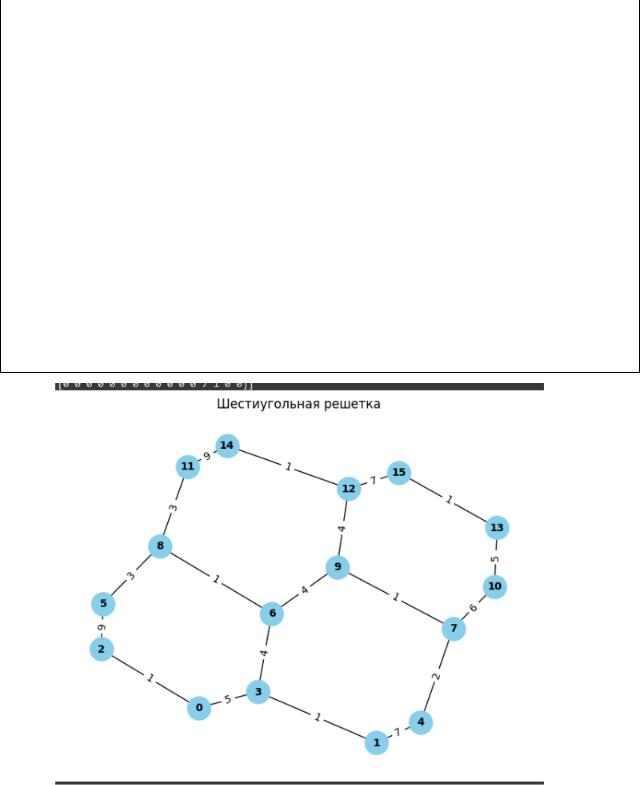
plt.title("Шестиугольная решетка") plt.show()
Рисунок 1- Взвешенная шестиугольная решетка

Листинг 2. Алгоритм поиска в глубину
def dfs(graph, current_node, goal, path=None, shortest=None, total_weight=0): if path is None:
path = [current_node]
# Вывод текущего пути print("Текущий путь:", path)
# Проверка на то, является ли текущий путь кратчайшим |
|
|
|||
if shortest is None or total_weight < shortest[1]: |
|
|
|||
# Если текущая вершина является целевой |
|
|
|||
if current_node == goal: |
|
|
|
|
|
shortest = (path, total_weight) |
# Обновление кратчайшего пути |
||||
print("Достигнута целевая вершина!") |
|
|
|||
print("Суммарный вес:", total_weight) |
|
|
|||
else: |
|
|
|
|
|
# Обход соседей текущей вершины |
|
|
|
||
for neighbor in graph.neighbors(current_node): |
|
|
|||
weight = graph[current_node][neighbor]['weight'] |
# Вес ребра |
||||
if neighbor not in path: |
# Проверка, была ли почсещена соседняя |
||||
вершина |
|
|
|
|
|
new_total_weight = total_weight + weight |
# Новый вес пути |
||||
# Рекурсивный вызов функции для соседней вершины |
|||||
new_path = dfs(graph, neighbor, goal, path + [neighbor], |
|||||
shortest, new_total_weight) |
|
|
|
|
|
if new_path: |
# |
Если |
найден новый |
путь, |
обновление |
кратчайшего пути |
|
|
|
|
|
shortest = new_path
return shortest
G = nx.from_numpy_array(matrix) start_node = 0
goal_node = 9
shortest_path, shortest_weight = dfs(G, start_node, goal_node)
print(f"Итоговый кратчайший путь от вершины {start_node} к вершине {goal_node} :", shortest_path)
print("Суммарный вес:", shortest_weight)
Выполняется проверка является ли текущий путь кратчайшим. Если путь меньше суммарного веса кратчайшего пути, и если текущая вершина равна целевой (goal), устанавливается новое значение кратчайшего пути.
Если текущая вершина не является целевой, производится рекурсивный обход соседей текущей вершины. Для каждого соседа, если он еще не посещен
(не находится в текущем пути), рассчитывается новый вес пути и вызывается рекурсивно алгоритм с обновленными параметрами.
Если новый путь короче текущего кратчайшего пути, он становится новым кратчайшим путем.
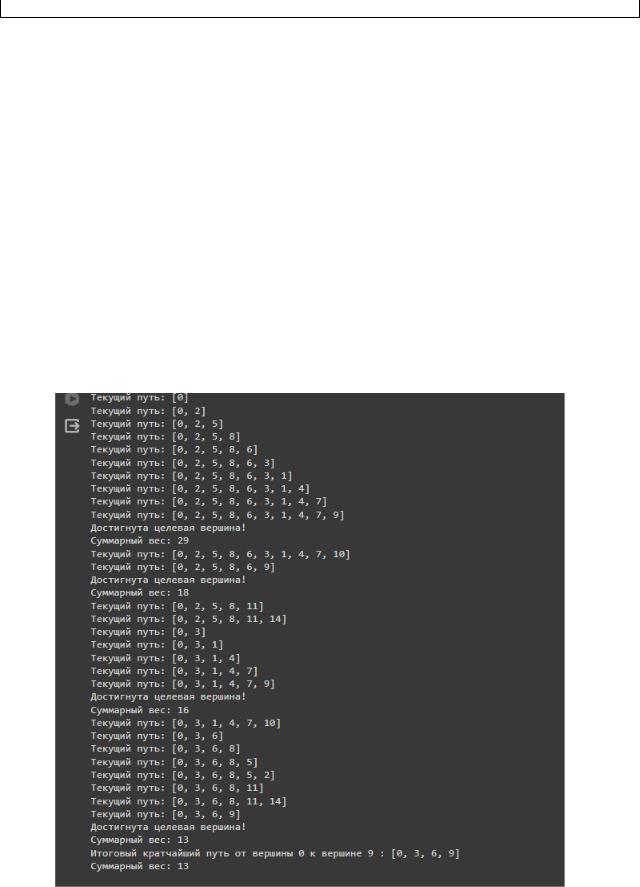
На рисунке 2 показан поиск пути от вершины 0 до вершины 9.
Рисунок 2- Путь от вершины 0 до вершины 9
Алгоритм посещает проходится по всем соседям посещенной вершины и, если достигнута целевая вершина выведен суммарный вес всего пути.
Итоговый кратчайший путь от вершины 0 до вершины 9: [0, 3, 6, 9] с весом:
13.
