анализ4

ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

Старший преподаватель				В.В. Боженко
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №4

КЛАСТЕРИЗАЦИЯ

по курсу: ВВЕДЕНИЕ В АНАЛИЗ ДАННЫХ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	4116
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2023

Цель работы: изучение алгоритмов и методов кластеризации на практике.

Вариант 1.

Ход работы

Часть 1. Простая линейная регрессия

Для создания набора данных использовалась функция make_data, которая создает датафрейм train с двумя числовыми столбцами x и y. Np.random.seed(seed): устанавливает зерно для генератора случайных чисел для воспроизводимости данных (рисунок 1,2).

Рисунок 1- Функция make_data создание датафрейма train

Рисунок 2- Датафрейм train

Также создается датафрейм test со значениями x и y (рисунок 3).

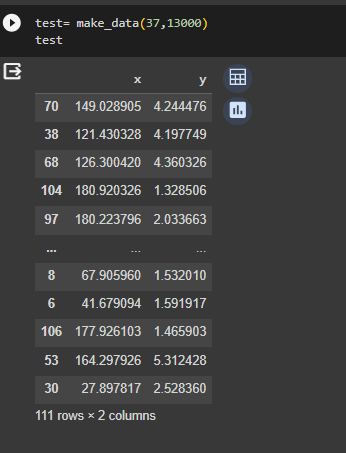
Рисунок 3- Создание датафрейма test

Выполнена стандартизация данных с использованием StandardScaler из библиотеки scikit-learn. Метод fit_transform преобразует значения признаков x и y таким образом, чтобы их среднее значение было близко к нулю, а стандартное отклонение было единичным (рисунок 4).

Рисунок 4- Стандартизация данных

Далее выполнялась кластеризация данных методом k-средних (KMeans) с тремя кластерами. Kmeans(n_clusters=3) создает модель k-средних с тремя кластерами. Kmeans.fit_predict(train[['x', 'y']]) выполняет обучение модели на данных x и y. Train['cluster'] добавляет столбец cluster, содержащий метки кластеров (рисунок 5).

Рисунок 5- Кластеризация данных методом k-средних, количество кластеров =3

Cтолбец cluster отображает кластер, к которому была отнесена каждая точка в результате применения алгоритма кластеризации методом k-средних.

Создан график, отображающий точки данных тренировочного набора. Каждая точка данных в этом графике покрашена в цвет, соответствующий её принадлежности к одному из кластеров. Точки, обозначающие центроиды, отмечены красными треугольниками, они представляют собой средние значения по каждому признаку в кластерах.Kmeans.cluster_centers_ извлекает значения координат x и y каждого центра кластера. (рисунок 6).

Рисунок 6- Кластеризация обучающих данных, количество кластеров=3

Данный график помогает визуально представить распределение данных в кластерах и местоположение центроидов относительно этих точек. По выведенному графику видно, что есть три кластера, отдаленных друг от друга.

Аналогично построен график для тестовых данных (рисунок 7).

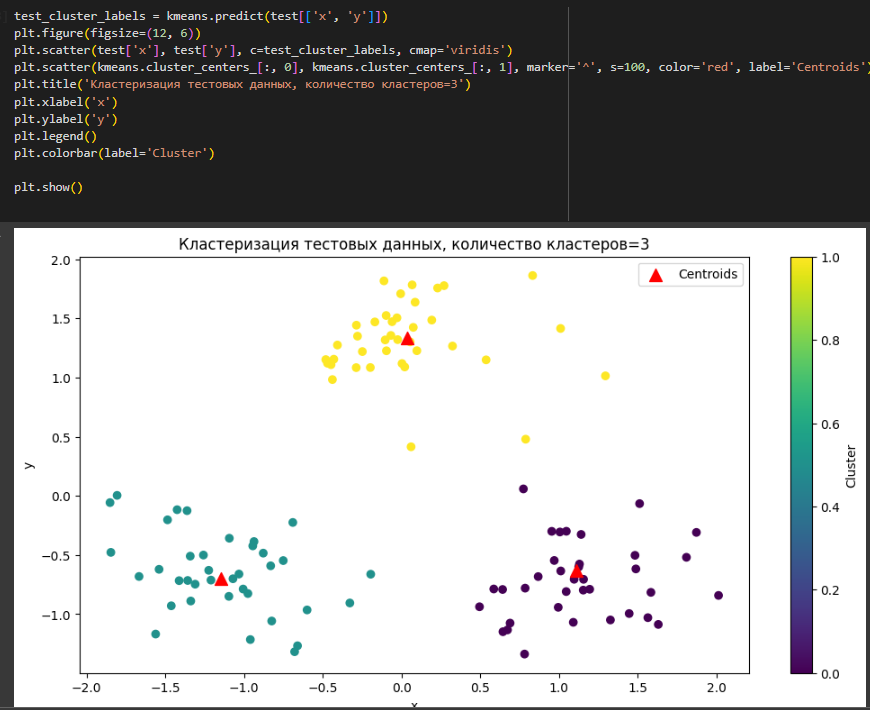
Рисунок 7- Визуализация кластерзации тестовых данных, количество кластеров=3

По графику с тестовыми данными, можно сказать, что есть небольшое различие с обучающими, центроиды находятся примерно в тех же местах.

Посчитан средний коэффициент силуэта (риснок 8).

Рисунок 8- Средний коэффициент силуэта, количество кластеров=3

Коэффициент силуэта измеряет насколько объект хорошо согласуется с кластером, к которому он был отнесен по сравнению с другими кластерами. В данном случае коэффициент силуэта равен 0.6867, что является довольно хорошим результатом. Это свидетельствует о том, что кластеры имеют хорошее разделение и объекты внутри них хорошо согласованы с соответствующими кластерами.

Аналогичным образом произведена кластеризация обучающих и тестовых данных методом k-средних с двумя кластерами (рисунок 9).

Рисунок 9 -Кластеризация данных методом k-средних, количество кластеров =2

Далее выполнена визуализация кластеризации обучающтх и тестовых даных (рисунок 10-12).

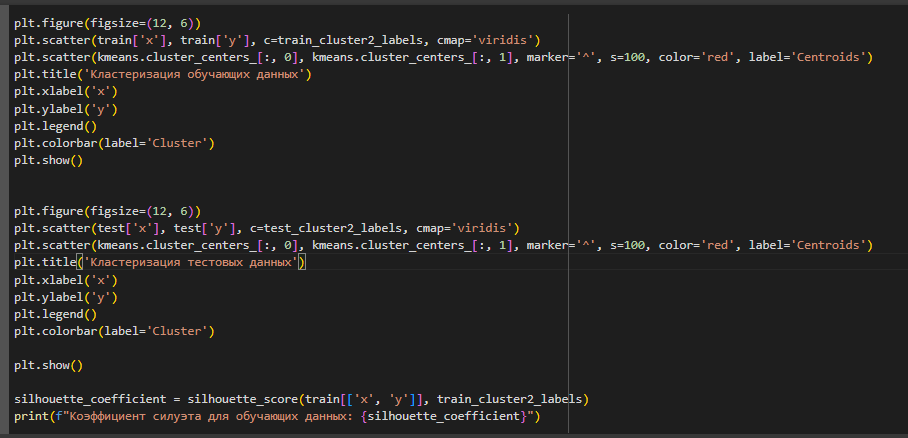
Рисунок 10- Визуализация кластеризации, количество кластеров =2

Рисунок 11- Кластеризация обучающих данных, количество кластеров=2

Рисунок 12- Кластеризация тестовых данных, количество кластеров=2

Из графиков можно заметить, что данные одного из кластеров имеют большой разброс, что свидетельствует о неверном выборе числа кластеров для кластеризации. Коэффициент силуэта, равный 0.4708, указывает на то, что кластеры в обучающих данных не столь однородны или разделены.

Затем произведена кластеризация обучающих и тестовых данных методом k-средних с четырьмя кластерами (рисунок 13)

Рисунок 13-Кластеризация данных методом k-средних, количество кластеров =4

И выполнялась визуализация кластеризации обучающих и тестовых даных с четырьмя кластерами (рисунок 14-16).

Рисунок 14- Визуализация кластеризации с четырьмя кластерами

Рисунок 15- Кластеризация обучающих данных, количество кластеров=4

Рисунок 16- Кластеризация тестовых данных, количество кластеров=4

Графики показывают, что два кластера соприкасаются, это может быть признаком, что данные имеют сложную структуру и границы между кластерами не являются четкими. Объектя обладают признаками, которые схожи с одноц и с другой группой, что затрудняет четкое и однозначное определение кластера, к которму они относятся. Коэффициент силуэта выше чем у кластеризации с двумя кластерами.

Для построения графика по методу локтя, алгоритм k-means применяется с различным количеством кластеров от 1 до 10 (рисунок 17-18). Метод локтя помогает определить оптимальное количество кластеров для модели KMeans. Он включает построение графика инерции (суммы квадратов расстояний от каждой точки данных до центроидов ближайших кластеров) относительно количества кластеров. Обычно на графике можно обнаружить точку перегиба, что указывает на оптимальное число кластеров.

Рисунок 17-Построение графика по методу локтя

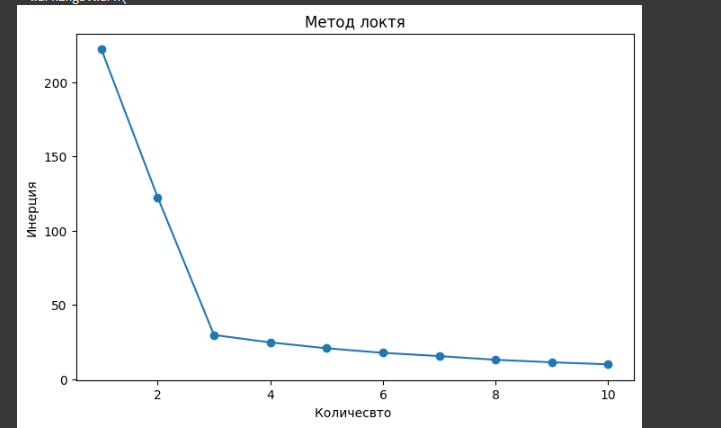
Рисунок 18- График по методу локтя

График локтя показывает, что оптимальное количество кластеров-3, так как третья точка находится на сгибе.

Загружен набор данных, который содержит информацию о сердечных болезнях (рисунок 19).

Рисунок 19- Загрузка набора данных

Произведена предварительная обработка данных. Для оценки данных использовался метод info (рисунок 20).

Рисунок 20- Оценка данных

Затем произведено удаление явных дубликатов (рисунок 21).

Рисунок 21- Удаление явных дубликатов

Для поиска неявных дубликатов применятся метод unique, который выводит уникальные значения (рисунок 22).

Рисунок 22- Поиск неявных дубликатов

Из столбца "Sex" выводится количество уникальных значений столбце.

Рисунок 23- Подсчет уникальных значений в столбце.

В столбце с полом пациентов есть одно значение, которое верояно всего является ошибочным и его следует исправить (рисунок 24).

Рисунок 24- Исправление значения

Столбец, который содержит информацию о холестерине, имеет одно значение с буквой, хотя все данные должны быть числовые. На рисунке 25 показано, что оно также было исправлено. Также используется метод isna(), который выводит количество пропусков в столбцах.

Рисунок 25- Изменение значения и вывод столбцов с пропусками

Пропуски в столбцах были удалены (рисунок 26).

Рисунок 26- Удаление сторк с пропусками

Целевой переменной выбран столбец HeartDisease, который показывает есть ли у пациента болезнь сердца, или нет.

Построена матрица диаграмм рассеяния по некоторым количественнным стобцам (рисунок 27).

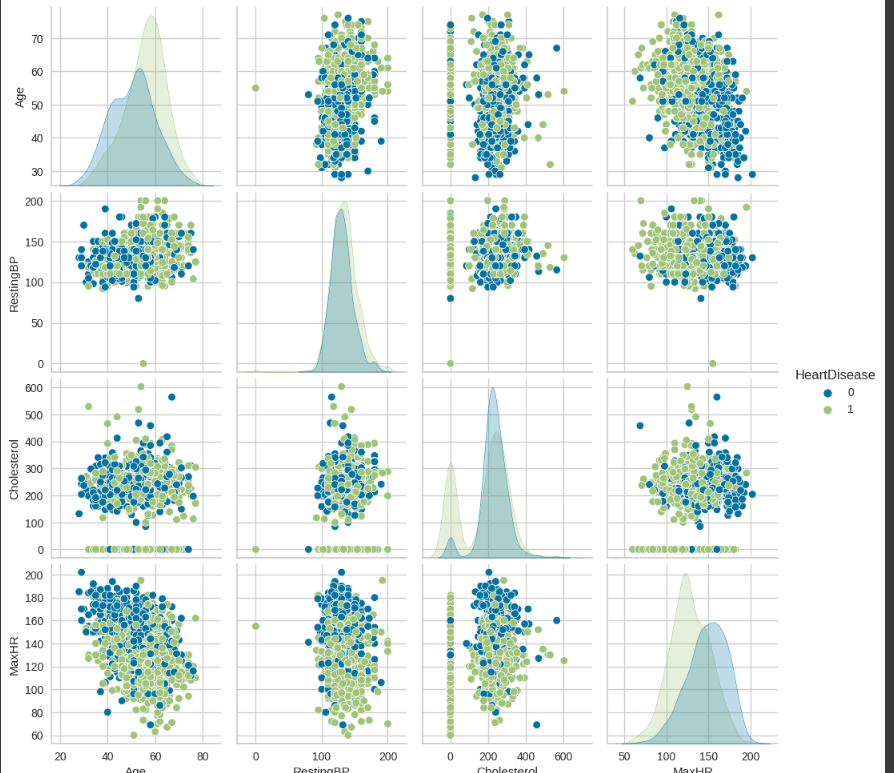
Рисунок 27- матрица диаграмм рассеяния

Диаграммы показывают, что пациенты от 60 до 70 лет в основном имеют какие-то заболевния снрдца. У больных пациентов достаточно невысокий пульс. Чем старше пациент, тем выше у него давыление, однако давление у больных пацтентов такое же, как и у здоровых.

Выполнялась стандартизация числовых данных без целевой переменной в DataFrame (рисунок 28).

Рисунок 28-Стандартизация числовых данных

Для подбора оптимального количества кластеров, построен график по методу локтя (рисунок 29,30).

Рисунок 29- Построение грфика по методу локтя

Рисунок 30- График по методу локтя

Смотря на график, непонятно сколько кластеров нужно использовать, поэтому для того, чтобы быстро визуализировать метод локтя используется визуализатор KElbowVisualizer (рисунок 31,32).

Рисунок 31- Использование визуализатора KElbowVisualizer

Рисунок 32- Визуализация метода локтя

Исходя из графика, оптимальное значение кластеров-4.

Тогда выполняется кластеризация для данных на основе четырех кластеров и выводится количество элементов, отнесенных к каждому кластеру (рисунок 33).

Рисунок 33- Кластеризация данных на основе четырех кластеров

Затем выполняется группировка данных по кластерам и выводятся средние значения для кадого числового столбца (рисунок 34).

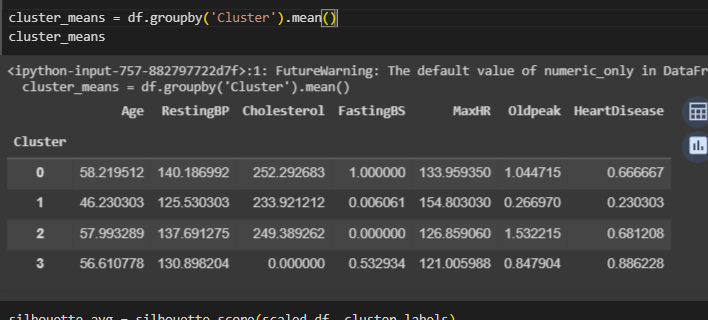
Рисунок 34- Создание датафрейма с истинными и предсказанными значениями

Кластер 0 имеет средний возраст пациентов 58 лет, уровень холестерина около 252, максимальный пульс около 134.

Вычислен средний коэффициент силуэта (рисунок 35).

Рисунок 35- Вычисление среднего коэффициента силуэта

Значение среднего коэффициента силуэта, равное примерно 0.222, указывает на умеренное, но не идеальное разделение данных на кластеры. Это говорит о том, что данные могут быть размытыми или иметь некоторые пересечения между кластерами.

Также вычислен индекс Калинского-Харабаса, который оценивает разделение кластеров, чем выше значение, тем четче разделение (рисунок 36).

Рисунок 36- Расчет индекса Калинского-Харабаса

Значение индекса, равное 212.12, говорит о том, что кластеры имеют хорошее разделение.

Далее для выполнения кластеризации иерархическим агломеративным методом, посторена дендограмма. Дендрограмма визуализирует процесс объединения кластеров, показывая, какие кластеры были объединены на каждом этапе и каково было расстояние между ними.

Рисунок 37- Модель k-ближайших соседей

Дендограмма позволяет визуально оценить подходящее количество кластеров, и показывает, что оптимальное количество кластеров -четыре.

Ссылка на Colab:

https://colab.research.google.com/drive/1p4r9DBmK1fWZvRVRIlrLyNleGxI7kgaT?usp=sharing

Вывод

В данной лабораторной работе выполнена кластеризация с использованием метода K-Means и иерархически агломеративного метода.

K-Means, примененный с использованием метода локтя, предоставил явный способ определения оптимального количества кластеров. Результаты визуализации с метками кластеров и выделенными центрами подчеркнули эффективность этого метода.

Иерархическая агломеративная кластеризация, позволяет лучше понять структуру данных через дендрограмму, однако, требует дополнительного усилия для определения оптимального числа кластеров. Она более гибкая в плане изменения количества кластеров и предоставляет визуальную наглядность.

Использование метрик, таких как Silhouette Score и Calinski-Harabasz помогло в объективной оценке результатов.