Часть 4. Решения задачи регрессии различными методами

Импортирован датафрейм car_price, с автомобилями и их характеристиками (рисунок 26).

Рисунок 26- Импортирование датасета car_price

Для предсказания выбрана переменная price, в контексте автомобильных данных она является интересующей. Для price построена гистограмма (рисунок 27).

Рисунок 27- Гистограмма по price

Гистограмма по столбцу price показывает, что наибольшее количество автомобилей имеют цену от 5000 до 10000, наименьшее - от 40000 до 45000.

Также по столбцу price построен boxplot (рисунок 28).

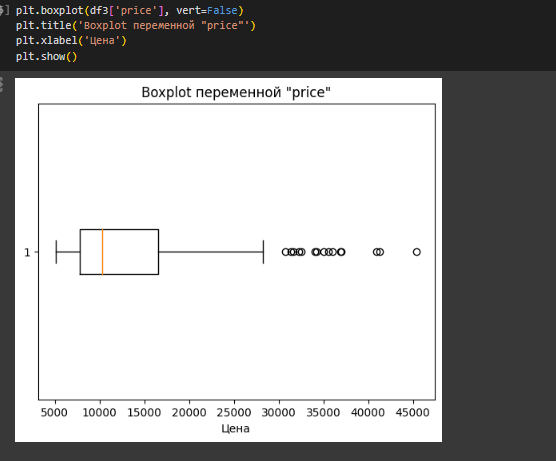
Рисунок 28- boxplot по price

Boxplot показывает, что медиана смещена влево, значит большее количество наблюдений находится ближе к минимальным значениям. Также наблюдается большое количество выбросов, которые указывают на то, что есть значения, которые находятся далеко от основных данных. Ящик показывает разброс данных.

Построена матрица диаграммы рассеяния с использованием pairplot для столбцов с размером машины, мощностью в лошадиных силах и ценой. Для раскраски столбцов используется столбец с названием автомобильной компании (рисунок 29).

Рисунок 29-матрица диаграммы рассеяния

Диаграммы показывают, что в основном самые дорогие автомобили у компании gas. Также у компании gas самые большие автомобили и самые мощные. Чем больше размер машины, тем больше цена. Если мощность машины увеличивается, то и цена также увеличивается.

Далее данные были разделены на обучающую и валидационную выборки. В данном случае в переменной X присваиваются значения, которые будут использоваться для обучения модели, присвоены все значения из всех числовых столбцов кроме car_ID и price. Y- переменная price, которую надо предсказать. Train_test_split разделяет данные на обучающую (X_train, Y_train) и тестовую (X_test, Y_test) выборки. Test_size=0.25 означает, что 25% данных будут отложены для тестирования. Установка random_state на 0 гарантирует, что при каждом запуске кода будут выбраны одни и те же случайные данные для обучающей и тестовой выборки (рисунок 30).

Рисунок 30- Разделение на обучающую и валидационную выборки

Создается переменная со всеми числовыми столбцами, кроме столбца с ID машины. Затем создается объект StandartScaler, который обучается на числовых данных, и затем эти данные заменяются нормализованными значениями. Таким образом весь датафрейм будет содержать нормализованные числовые данные (рисунок 31).

Рисунок 31- Нормализация числовых данных с помощью StandartScaler

Создана и обучена на основе входных данных модель линейной регрессии (рисунок 32).

Рисунок 32- Создание и обучение простой модели линейной регрессии на выходных данных

Для осуществления подбора оптимальных параметров, из библиотеки sklearn импортируется GridSearchCV. Создается сетка параметров Param_grid(), которые GridSearchCV будет исследовать, чтобы найти лучшие параметры для линейной регрессии. Fit_intercept указывает будет ли модель иметь параметр смещения. Positive указывает, можно ли принимать во внимание только положительные коэффициенты при оценке модели линейной регрессии. Создается объект GridSearchCV с указанием модели, сетки параметров param_grid, количества блоков перекрестной проверки (cv=5), и метрика по отрицательному среднеквадратичному отклонению (scoring='neg_mean_squared_error'). Best_params содержит лучшие значения параметров, найденные в процессе поиска. Best_model содержит лучшую модель, обученную с лучшими параметрами (рисунок 33).

Рисунок 33- Подбор оптимальных параметров с GridSearchCV

Предсказаны значения и для оценки качества модели вычислены метрики (рисунок 34).

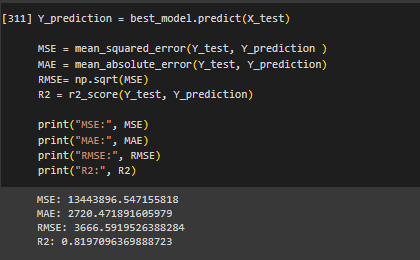
Рисунок 34- Предсказание значений и вычисление метрик

Среднеквадратичное отклонение, среднее абсолютное отклонение, стандартное отклонение ошибок модели очень велики. Коэффициент детерминации близок к 1, что указывает на хорошую предсказательную способность модели.

Создан датафрейм с истинными и предсказанными значениями (рисунок 35).

Рисунок 35- Создание датафрейма с истинными и предсказанными значениями

Взглянув на данные, можно сказать, что предсказания имеют как положительные, так и отрицательные отклонения от фактических значений. В 4 строке предсказанная цена -405.60, тогда как фактическая цена 5151.0. Это указывает на значительное отклонение предсказанной цены от истинной. Но многие предсказания близки к фактическим.

Создан и выведен датафрейм с признаками и их коэффициентами (рисунок 36).

Рисунок 36- Датафрейм с признаками и их коэффициентами

Symboling, carwidth, carheight , enginesize, boreratio, compressionratio, horsepower и peakrpm имеют положительные коэффициенты, что означает, что увеличение этих признаков приводит к увеличению цены. Wheelbase, curbweight также влияют, но их влияние немного меньше. Carlength, stroke, citympg и highwaympg имеют нулевые коэффициенты, что означает, что эти признаки, слабо влияют или вообще не влияют на целевую переменную в данной модели.

Для визуализации создан график с истинными и предсказанными значениями (рисунок 37).

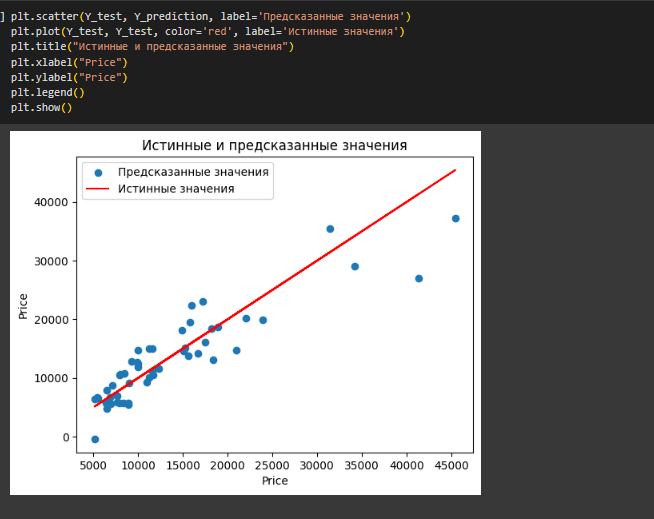
Рисунок 37- График с истинными и предсказанными значениями

Из графика видно, что есть выбросы, которые указывают, что модель может допускать неточные прогнозы для определенных значений. Однако, основная часть предсказанных значений близка к истинным.

Метод k-ближайших соседей предсказывает значение для нового наблюдения, на основе значений его ближайших соседей. Для реализации регрессии методом k-ближайших соседей, создана и обучена модель k-ближайших соседей, посчитаны метрики, реализован график (рисунок 38).

Рисунок 38- Модель k-ближайших соседей

График показывает, что также есть выбросы, но предсказанные значения стали ближе к истинным, по сравнению с прошлой моделью. Среднеквадратичное отклонение, среднее абсолютное отклонение, стандартное отклонение ошибок модели велики. R2 показывает, что модель объясняет около 79.8% дисперсии целевой переменной, что можно считать приемлемым.

Модель дерева решений представляет собой структуру, где каждый узел представляет собой "вопрос" о некотором признаке данных, а каждая ветвь - ответ на этот вопрос. Цель состоит в том, чтобы последовательно разделять данные на наиболее однородные подгруппы (листья) по признакам, чтобы в конечном итоге получить точные прогнозы. Создана и обучена модель дерева решений. Вычислены метрики, построен график отображения регрессии. Max_depth используется для указания максимальной глубины дерева (рисунок 39).

Рисунок 39- Модель дерева решений

По сравнению с моделью k-ближайших соседей, среднеквадратичное отклонение, среднее абсолютное отклонение, стандартное отклонение ошибок модели стали меньше. Модель объясняет около 87% дисперсии целевой переменной, что заметно больше. Также по графику видно, что выбросов стало меньше.

Для подведения итогов, все графики моделей показаны наи одном.

Рисунок 40-Графики 3-ех моделей

Исходя из графиков и метрик, можно подвести итог, что модель дерева реешний является самой точной из рассматриваемых моделей, она имеет самые низкие ошибки, и объясняет больший процент дисперсии целевой переменной. Также модель дерева решений имеет наименьшее количество выбросов

Ссылка на Colab:

https://colab.research.google.com/drive/1R7zsTaCwxXilZWwtBSCzhRhocbzpl9yf?usp=sharing

Вывод

В ходе выполнения лабораторной работы обучена модель простой линейной регрессии и множественной линейной регрессии с двумя предикторами. Реализована и обучена модель полиномиальной регрессии, которая показала, чем больше степень полинома для модели, тем больше предсказанные значения похожи на истинные.

Было произведено обучение модели k-ближайших соседей, дерева решений, и простой линейной регрессии на одних данных. Самой подходящей для рассматриваемых данных оказалась модель дерева решений. Также для оценки качества предсказания для всех моделей вычислены метрики, и построены графики для визуализации регрессии.