Построить в масштабе четыре графика фпв мгновенных значений и огибающих угп, и суммы гармонического сигнала с угп.
Закон распределения огибающей гауссовской помехи
(34)
ФПВ мгновенных значений принятого сигнала
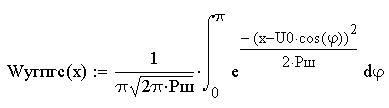(35)
Рисунок 17- График ФПВ мгновенных значений шума и суммы сигнал+шум
ФПВ сигнала и шума:
огибающая гауссовской помехи, распределенная по закону Релея
(36)
огибающая принимаемой суммы гармонического сигнала + УГП, подчиняющаяся обобщенному распределению Релея
(37)
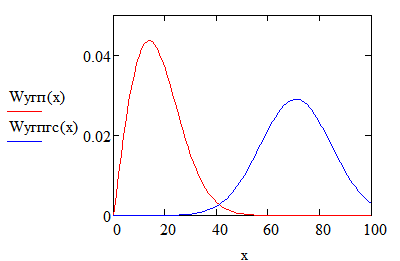
Рисунок 18- График ФПВ огибающей шума и суммы сигнал+шум
9. С учетом заданного вида приема (детектирования) сигнала дискретной модуляции:
Рассчитать среднюю вероятность ошибки в двоичном дкс, скорость передачи информации по двоичному симметричному дкс. Показатель эффективности передачи сигнала дискретной модуляции по нкс;
За количественную меру помехоустойчивость в системах электросвязи принимают среднюю на бит вероятность ошибки: Рош.ср.=Р(0)Р(1/0)+Р(1)Р(0/1).
При равенствах априорных вероятностей Р(0)=Р(1)=0.5, а также условных вероятностей Р(1/0)=Р(0/1)=Рош (условие симметричности двоичного ДКС), средняя на бит вероятность ошибки равна Рош.ср.=Рош.
средняя вероятность ошибки при некогерентном приеме сигналов ДЧМ
(38)
энтропия ошибочных решений (бит)
(39)
длительность посылки (с)
(40)
скорость передачи информации (бит/с)
(41)
показатель эффективности системы передачи
(42)
Изобразить схему приемника сигналов дискретной модуляции и коротко описать принцип его работы, пояснить случаи, когда он выносит ошибочные решения.
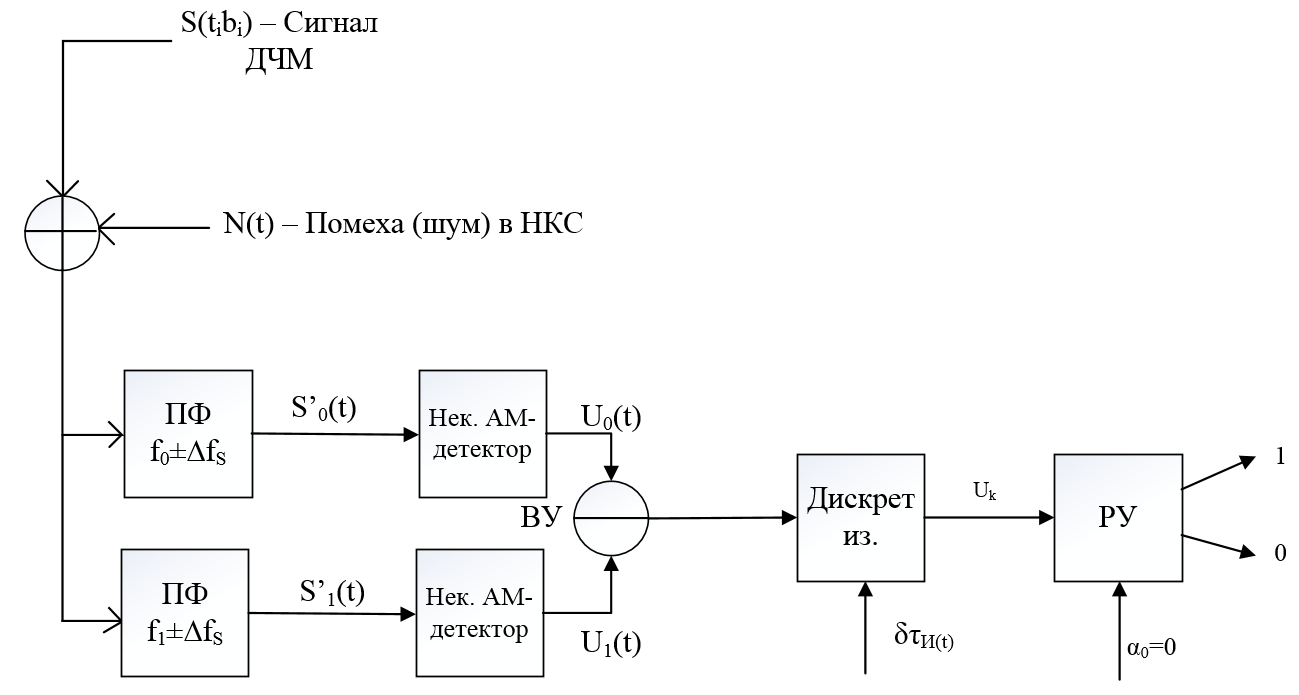
Рисунок 19- Схема приемника сигналов ДЧМ
Полосовые
фильтры на входе приемника ДЧМ выделяют
сигналы с частотами
или
,
соответствующие передаче «0» или «1».
Пусть по каналу связи передается сигнал
с частотой
Тогда через ПФ, настроенный на частоту
проходит сумма сигнала и помехи N(t).
А через другой ПФ проходит только помеха.
В канале, с сигналом амплитудный детектор
выделяет огибающую сигнала и помехи,
распределенной по обобщенному закону
Рэлея (Райса). В канале с помехой детектор
выделяет огибающую только помехи,
которая распределена по обычному закону
Рэлея. Если помеха достаточно мала, то
напряжение на выходе детектора канала
с помехой будет меньше напряжения на
выходе канала с сигналом и помехой.
Следовательно их разность в вычитающем
устройстве (ВУ) окажется положительной
и решающее устройство выдаст 1. При
сильной помехе напряжение на выходе
детектора канала без сигнала может
стать больше, чем напряжение на выходе
детектора канала с сигналом, их разность
в ВУ окажется отрицательной и решающее
устройство ошибочно выдаст 0.
10. Рассматривая отклик декодера пру как случайный дискретный сигнал на выходе -ичного дкс:
рассчитать распределение вероятностей дискретного сигнала на выходе декодера, скорость передачи информации по L-ичному ДКС, относительные потери в скорости передачи информации по -ичного ДКС;
Рассчитаем распределение вероятностей дискретного сигнала на выходе декодера:
вероятность правильного приема
(43)
Таблица 9-Распределение вероятностей дискретного сигнала на выходе детектора:
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
0.0013 |
0.0214 |
0.1359 |
0.3413 |
0.3413 |
0.1359 |
0.0214 |
0.0013 |
|
|
0.0018 |
0.0218 |
0.1359 |
0.3405 |
0.3405 |
0.1359 |
0.0218 |
0.0018 |
|
Определим скорость передачи информации по L-ичному ДКС:
энтропия восстановленного L-ичного сообщения (бит)
(44)
скорость передачи информации (бит/сек)
(45)
Зная производительность H`y L-ичного источника (скорость ввода информации в ДКС) и скорость передаваемой по ДКС информации RL, найдем величину относительных потерь в скорости:
(46)
б) построить в масштабе график закона распределения вероятностей отклика декодера и сравнить его с законом распределения вероятностей отклика квантователя.
Рисунок 20- График закона распределения вероятностей отклика декодера
Из-за шума в канале передачи возрастает дисперсия принимаемого случайного сигнала, что видно по увеличению вероятности при pвых(1) и pвых(6).