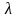МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ СВЯЗИ И

МАССОВЫХ КОММУНИКАЦИЙ

Ордена трудового Красного Знамени федеральное государственное бюджетное

образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Кафедра «Информатика»

Лабораторная работа №7

по дисциплине «Численные методы»

на тему

«Методы многомерной оптимизации»

Проверил:

Москва, 2024

Содержание

1.Постановка задачи 2

2.Проверка условия существования точки минимума заданной функции f(x,y) 3

3.Решение задачи многомерной оптимизации аналитическим методом 4

4.Выбор начальной точки x₀, y₀ итерационного процесса оптимизации 4

5.Ручной расчёт градиентным методом с дроблением шага 4

6.Программный расчёт методом наискорейшего спуска с точностью 10^-4 5

7.Построение траекторий спуска методов ГДШ и НСЧ 9

8.Оптимизация с помощью функции minimize пакета Mathcad 10

9.Выводы 11

1.Постановка задачи

1.Выбрать индивидуальное задание из таблицы для решения задачи оптимизации функции двух переменных:

Функцию –f(x, y);

Методы, заданные для ручного расчета и для расчета на компьютере.

№	Целевая функция	Ручной	Программа
25	f(x,y) = 3 x2 + 2 y2 – 5 y + 1	ГДШ	НСА

2.Проверить условия существования точки минимума заданной функции f(x,y).

3.Решить задачу многомерной оптимизации аналитическим методом.

4.Выбрать начальную точку x₀, y₀ итерационного процесса оптимизации.

5.Провести расчет 3-х итераций 1-м заданным методом, а результаты расчета свести в таблицу.

6.Написать программу получения координат минимума функции 2-м заданным методом с точностью 10^-4, результаты расчета свести в таблицу.

7.Используя данные 3-х итераций, построить в одном графическом окне две траектории спуска (НСА и ГДШ) и сделать вывод о правильности проведенных расчетов.

8.Решить задачу многомерной оптимизации с использованием функции minimize пакета Mathcad, сравнить полученные координаты точки минимума, вычисленные с использованием пакета, с координатами, полученными аналитическим методом.

2.Проверка условия существования точки минимума заданной функции f(x,y)

Функция: f(x,y) = 3 x² + 2 y² – 5 y + 1

Проверка условия существования точки минимума заданной функции f(x,y):

Матрица Гессе:

Угловые миноры:

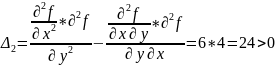
Условия существования точки минимума заданной функции выполняются.

3.Решение задачи многомерной оптимизации аналитическим методом

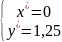
-2,125

4.Выбор начальной точки x₀, y₀ итерационного процесса оптимизации

Выберем начальную точку спуска - x₀ = 0.5, y₀ = 1

5.Ручной расчёт градиентным методом с дроблением шага

Результаты расчёта трёх итераций:

k	x	y
0	0.5	1	-1.25	3	-1	0.125
1	0.125	1.125	-2.046875	0.75	-0.5	0.125
2	0.03125	1.1875	-2.1142578	0.1875	-0.25	0.125
3	7.8125*10-3	1.21875	-2.1228638	0.046875	-0.125	0.125

Значение минимума после трёх итераций в точке (7.8125*10^-3; 1.21875) равно -2.1228638.

6.Программный расчёт методом наискорейшего спуска с точностью 10^-4

import math

def Q(x, y):

return 3 * math.pow(x, 2) + 2 * math.pow(y, 2) - 5 * y + 1

def P(x):

return 6 * x

def S(y):

return 4 * y - 5

def F(x, y, lam):

return Q(x - lam * P(x), y - lam * S(y))

def zs(x, y, E):

k1, k2, lam, lam1, lam2, f1, f2 = 0, 0, 0, 0, 0, 0, 0

a, b = 0, 1

k1 = (3 - math.sqrt(5.0)) / 2

k2 = (math.sqrt(5.0) - 1) / 2

lam1 = a + k1 * (b - a)

lam2 = a + k2 * (b - a)

f1 = F(x, y, lam1)

f2 = F(x, y, lam2)

while (b - a) > E:

if f1 < f2:

b = lam2

lam2 = lam1

lam1 = a + k1 * (b - a)

f2 = f1

f1 = F(x, y, lam1)

else:

a = lam1

lam1 = lam2

lam2 = a + k2 * (b - a)

f1 = f2

f2 = F(x, y, lam2)

return (a + b) / 2

def HC(x, y, E, min_iters=15):

lam, f = 0, 0

iterations = 0

print(f"Initial: x = {x}; y = {y}; f(x,y) = {Q(x, y)}; g1 = {P(x)}; g2 = {S(y)}; lambda = {zs(x, y, E)};")

while (iterations < min_iters) or (abs(P(x)) > E and abs(S(y)) > E):

iterations += 1

lam = zs(x, y, E)

x = x - lam * P(x)

y = y - lam * S(y)

f = Q(x, y)

print(f"x = {x}; y = {y}; f(x,y) = {f}; g1 = {P(x)}; g2 = {S(y)}; lambda = {lam};")

lam = zs(x, y, E)

x = x - lam * P(x)

y = y - lam * S(y)

f = Q(x, y)

print(f"Final: x = {x}; y = {y}; f(x,y) = {f}; g1 = {P(x)}; g2 = {S(y)}; final iteration;")

def main():

while True:

x, y, E = 0, 0, 0

x = float(input("Введите x0: "))

y = float(input("Введите y0: "))

E = float(input("Введите погрешность E: "))

HC(x, y, E)

repeat = input("\nДля повтора нажмите '1': ")

if repeat != '1':

break

if __name__ == "__main__":

main()

Результат работы кода:

k	x	y	f(x, y)
0	0.5	1.0	-1.25	3.0	-1.0	0.172415
1	-0.017246177	1.17241539	-2.1120689	-0.103477065	-0.310338430	0.172415
2	0.0073903165	1.2463028	-2.1248088	0.044341898	-0.014788846	0.238086
3	-0.000254909	1.2488526	-2.1249971	-0.001529456	-0.00458955	0.172415
4	0.0001092335	1.24994532	-2.1249999	0.000655401	-0.00021871	0.238086
5	-3.76772*10-6	1.24998303	-2.124999999381551	-2.26063*10-5	-6.78741*10-5	0.172415
6	1.616959*10-6	1.24999919	-2.124999999990872	9.70175*10-6	-3.20542*10-6	0.238193
7	-6.26404*10-8	1.24999975	-2.1249999999998663	-3.75842*10-7	-9.85691*10-7	0.173123
8	2.5375*10-8	1.24999998	-2.124999999999998	1.52250*10-7	-6.23680*10-8	0.234181
9	-6.8941*10-9	1.24999999	-2.1249999999999996	-4.13648*10-8	-9.49282*10-9	0.211948
10	6.72942*10-9	1.2500000007532683	-2.125	4.03765*10-8	3.01307*10-9	0.329351
11	8.27574*10-10	1.2500000003128466	-2.125	4.96544*10-9	1.25138*10-9	0.146170
12	-3.8267*10-9	1.24999999	-2.1249999999999996	-2.29602*10-8	-3.44048*10-9	0.937335
13	4.96186*10-9	1.2500000004568042	-2.125	2.977118*10-8	1.82721*10-9	0.382773
14	-2.1667*10-9	1.2500000000192848	-2.1250000000000004	-1.30003*10-8	7.71391*10-11	0.239445
15	6.65763*10-9	1.2499999999669242	-2.125	3.99458*10-8	-1.3230*10-10	0.678779
16	-8.680937*10-9	1.2500000000177265	-2.124999999999999	-5.20856*10-8	7.09059*10-11	0.812629

7.Построение траекторий спуска методов ГДШ и НСЧ

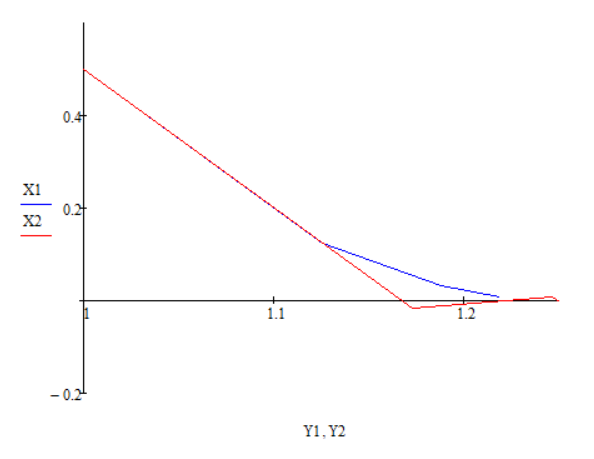
Оба метода стремятся к точке (0, 1.25), что свидетельствует о правильности проведённых расчётов

8.Оптимизация с помощью функции minimize пакета Mathcad

Точка локального минимума согласно функции minimize: -2.125 , что входит в рамки полученные градиентными методами и совпадает с аналитическим решением.

9.Выводы

	k	x	y	f(x, y)
Метод с дроблением шага	3	7.8125*10-3	1.219	-2.122864	0.046875	-0.125	0.125
Метод с наискорейшим спуском	16	-8.680937*10-9	1.25	-2.124999	-5.209*10-8	7.091*10-11	0.813
Функция minimize	-	2.4266894*10-11	1.25	-2.125	1.456*10-10	0	-

В ходе выполнения лабораторной работы были получены приблизительные значения точки локального минимума функции f(x,y) = 3 x² + 2 y² – 5 y + 1 градиентными методами с дроблением шага и наискорейшего спуска. Результаты методов сошлись с машинном решением в рамках погрешности.