МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ СВЯЗИ И

МАССОВЫХ КОММУНИКАЦИЙ

Ордена трудового Красного Знамени федеральное государственное бюджетное

образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Кафедра «Информатика»

Лабораторная работа №6

по дисциплине «Численные методы»

на тему

«Одномерная оптимизация»

Проверил:

Москва, 2024

Содержание

1.Постановка задачи 2

2.Исследование индивидуального варианта задания 3

3.Метод золотого сечения 6

4.Метод дихотомии 13

5.Вычислить число итераций, необходимых, чтобы локализовать точку минимума с точностью E1 = 10^-4 методами дихотомии и золотого сечения. 14

6.Оптимизация с помощью пакета Mathcad 16

7.Выводы 16

1.Постановка задачи

1.Выбрать индивидуальное задание по номеру варианта из табл. 5-1 для решения задачи одномерной оптимизации: функцию f(x), минимум которой необходимо найти.

2.Провести исследование индивидуального варианта задания: построить график функции , выбрать начальный отрезок неопределенности (отрезок, содержащий точку минимума), проверить выполнение аналитического условия унимодальности функции на выбранном отрезке.

3.Создать в сценарии функцию для проведения значений 3-х итераций определить длину отрезка, содержащего точку минимума, после трех итераций.

4.Написать и выполнить программу, реализующую программу метода, вычисляющую координаты точки минимума функции с заданной точностью 10^-4.

5.Вычислить число итераций, необходимых, чтобы локализовать точку минимума с точностью E1 = 10^-4 методами дихотомии и золотого сечения.

6.Решить задачу оптимизации с использованием функции minimize пакета Mathcad.

№ вар.	Целевая функция
25	f(x) = sin(2x) – x

2.Исследование индивидуального варианта задания

График функции, построенный на достаточно большом отрезке ОДЗ функции:

Выберем по построенному графику функции начальный отрезок неопределенности (отрезок, содержащий точку минимума): отрезок [2.4;2.8]

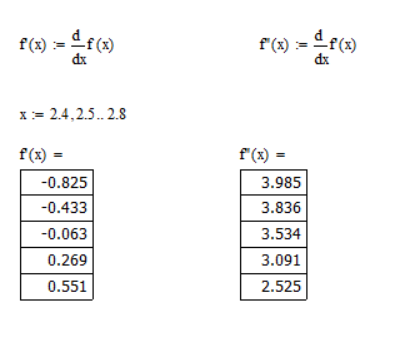
Проверим унимодальность функции на данном отрезке:

х	2.4	2.5	2.6	2.7	2.8
f’(x)	-0.825002	-0.4326756	-0.0629667	0.2693858	0.5511318
f’’ (x)	3.9846584	3.8356971	3.5338186	3.091058	2.5250666

Так как производная от функции меняет знак с минуса на плюс один раз, и производная второго порядка больше нуля на всей длине, отрезок содержит точку минимума, следовательно функция на выбранном отрезке – унимодальна.

3.Метод золотого сечения

Проведём расчёт трёх итераций методом золотого сечения в программе Mathcad:

Результаты работы:

N	a	b	x1	x2	f(x1)	f(x2)	Δn
0	2.4	2.8	2.5528	2.6472	-3.4764	-3.4825	0.2472
1	2.5528	2.8	2.6472	2.7055	-3.4825	-3.4712	0.1528
2	2.5528	2.7055	2.6111	2.6472	-3.4839	-3.4825	0.0944
3	2.5528	2.6472

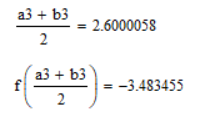
Проведём расчёт методом золотого сечения с помощью программы:

import math

a = 2.4

b = 2.8

E = 0.0001

def Q(x):

return math.sin(2 * x) - x

k2 = (-1 + math.sqrt(5)) / 2

k1 = 1 - k2

x1 = a + k1 * (b - a)

x2 = a + k2 * (b - a)

Q1 = Q(x1)

Q2 = Q(x2)

iteration_count = 0

while abs(b - a) > E:

iteration_count += 1

print(f"Текущие значения: a={a}, b={b}, x1={x1}, x2={x2}, Q1={Q1}, Q2={Q2}, Длина интервала={b-a}")

if Q1 > Q2:

a = x1

x1 = x2

Q1 = Q2

x2 = a + k2 * (b - a)

Q2 = Q(x2)

else:

b = x2

x2 = x1

Q2 = Q1

x1 = a + k1 * (b - a)

Q1 = Q(x1)

min_x = (a + b) / 2

min_Q = Q(min_x)

print(f"Итоговые значения: a={a}, b={b}, x1={x1}, x2={x2}, Q1={Q1}, Q2={Q2}, Длина интервала={b-a}")

print(f'Минимум в точке x={min_x} равен {min_Q} с точностью {E}')

print(f'Всего итераций: {iteration_count}')

Результат работы кода:

1 итерация

Текущие значения: a=2.4, b=2.8, x1=2.5527864045000417, x2=2.6472135954999576, Q1=-3.476480323858287, Q2=-3.4825575205243195, Длина интервала=0.3999999999999999

2 итерация

Текущие значения: a=2.5527864045000417, b=2.8, x1=2.6472135954999576, x2=2.705572809000084, Q1=-3.4825575205243195, Q2=-3.471215400914123, Длина интервала=0.24721359549995814

3 итерация

Текущие значения: a=2.5527864045000417, b=2.705572809000084, x1=2.611145618000168, x2=2.6472135954999576, Q1=-3.4839378380612103, Q2=-3.4825575205243195, Длина интервала=0.15278640450004222

4 итерация

Текущие значения: a=2.5527864045000417, b=2.6472135954999576, x1=2.5888543819998313, x2=2.611145618000168, Q1=-3.48253250364272, Q2=-3.4839378380612103, Длина интервала=0.09442719099991592

5 итерация

Текущие значения: a=2.5888543819998313, b=2.6472135954999576, x1=2.611145618000168, x2=2.624922359499621, Q1=-3.4839378380612103, Q2=-3.483936359715878, Длина интервала=0.058359213500126295

6 итерация

Текущие значения: a=2.5888543819998313, b=2.624922359499621, x1=2.6026311234992843, x2=2.611145618000168, Q1=-3.4836081081998986, Q2=-3.4839378380612103, Длина интервала=0.03606797749978963

7 итерация

Текущие значения: a=2.6026311234992843, b=2.624922359499621, x1=2.611145618000168, x2=2.6164078649987377, Q1=-3.4839378380612103, Q2=-3.4840149222548535, Длина интервала=0.022291236000336667

8 итерация

Текущие значения: a=2.611145618000168, b=2.624922359499621, x1=2.6164078649987377, x2=2.6196601125010512, Q1=-3.4840149222548535, Q2=-3.4840144761068945, Длина интервала=0.01377674149945296

9 итерация

Текущие значения: a=2.611145618000168, b=2.6196601125010512, x1=2.614397865502481, x2=2.6164078649987377, Q1=-3.483996853193108, Q2=-3.4840149222548535, Длина интервала=0.008514494500883263

10 итерация

Текущие значения: a=2.614397865502481, b=2.6196601125010512, x1=2.6164078649987377, x2=2.6176501130047947, Q1=-3.4840149222548535, Q2=-3.4840190770648523, Длина интервала=0.0052622469985701414

11 итерация

Текущие значения: a=2.6164078649987377, b=2.6196601125010512, x1=2.6176501130047947, x2=2.6184178644949943, Q1=-3.4840190770648523, Q2=-3.4840189704654208, Длина интервала=0.0032522475023135655

12 итерация

Текущие значения: a=2.6164078649987377, b=2.6184178644949943, x1=2.6171756164889377, x2=2.6176501130047947, Q1=-3.4840181217130604, Q2=-3.4840190770648523, Длина интервала=0.002009999496256576

13 итерация

Текущие значения: a=2.6171756164889377, b=2.6184178644949943, x1=2.6176501130047947, x2=2.6179433679791373, Q1=-3.4840190770648523, Q2=-3.484019277356933, Длина интервала=0.0012422480060565455

14 итерация

Текущие значения: a=2.6176501130047947, b=2.6184178644949943, x1=2.6179433679791373, x2=2.618124609520651, Q1=-3.484019277356933, Q2=-3.4840192521754054, Длина интервала=0.0007677514901995863

15 итерация

Текущие значения: a=2.6176501130047947, b=2.618124609520651, x1=2.6178313545463086, x2=2.6179433679791373, Q1=-3.484019236022906, Q2=-3.484019277356933, Длина интервала=0.0004744965158565151

16 итерация

Текущие значения: a=2.6178313545463086, b=2.618124609520651, x1=2.6179433679791373, x2=2.6180125960878224, Q1=-3.484019277356933, Q2=-3.4840192811690835, Длина интервала=0.00029325497434262715

17 итерация

Текущие значения: a=2.6179433679791373, b=2.618124609520651, x1=2.6180125960878224, x2=2.6180553814119665, Q1=-3.4840192811690835, Q2=-3.48401927522431, Длина интервала=0.00018124154151388794

18 итерация

Текущие значения: a=2.6179433679791373, b=2.6180553814119665, x1=2.6179861533032813, x2=2.6180125960878224, Q1=-3.48401928167258, Q2=-3.4840192811690835, Длина интервала=0.0001120134328291833

Минимум в точке x=2.61797798203348 равен -3.484019281338273 с точностью 0.0001

Всего итераций: 18

N	a	b	x1	x2	f(x1)	f(x2)	Δn
1	2.4	2.8	2.55279	2.64721	-3.47648	-3.48255	0.4
2	2.55	2.8	2.64721	2.70557	-3.48256	-3.47122	0.247
3	2.55	2.70	2.61115	2.64721	-3.48394	-3.48256	0.152
4	2.55	2.65	2.58885	2.61115	-3.48253	-3.48394	0.094
5	2.59	2.65	2.61115	2.62492	-3.48394	-3.48394	0.058
6	2.59	2.62	2.60263	2.61115	-3.48360	-3.48394	0.036
7	2.60	2.62	2.61115	2.61641	-3.48394	-3.48401	0.022
8	2.61	2.62	2.61641	2.61966	-3.48401	-3.48401	0.014
9	2.61	2.62	2.61439	2.61641	-3.48399	-3.48401	0.009
10	2.61	2.62	2.61641	2.61765	-3.48401	-3.48402	0.005
11	2.61	2.61	2.61765	2.61842	-3.48402	-3.48402	0.003
12	2.61	2.61	2.61718	2.61765	-3.48402	-3.48402	0.002
13	2.61	2.61	2.61765	2.61794	-3.48402	-3.48402	0.001
14	2.61	2.61	2.61794	2.61812	-3.48402	-3.48402	0.0008
15	2.61	2.61	2.61783	2.61794	-3.48402	-3.48402	0.0005
16	2.61	2.61	2.61794	2.61802	-3.48402	-3.48402	0.0003
17	2.61	2.61	2.61802	2.61806	-3.48402	-3.48402	0.0002
18	2.61	2.61	2.61799	2.61801	-3.48402	-3.48402	0.0001

Минимум в точке x=2.61797798203348 равен -3.484019281338273 с точностью 0.0001

Всего итераций: 18