МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ СВЯЗИ И

МАССОВЫХ КОММУНИКАЦИЙ

Ордена трудового Красного Знамени федеральное государственное бюджетное

образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Кафедра «Информатика»

Лабораторная работа №5

по дисциплине «Численные методы»

на тему

«Методы решения ОДУ»

Проверил:

Москва, 2024

Содержание

Постановка задачи 2

1.Точное аналитическое решение заданного дифференциального уравнения 3

3

2.Значения точного решения ОДУ 4

3.Численное решение заданного ОДУ методом Эйлера. 5

4.Значения погрешностей метода Эйлера 5

6.Значения погрешностей метода Рунге-Кутта 4-го порядка с точностью 10^-4 8

7.Решение дифференциального уравнения y^s(x) использованием функции математического пакета. 9

8.Иллюстрированные решения y(x), y^э(x), y^pk(x) в одной системе координат 9

Выводы 10

Постановка задачи

№ вар	Уравнение	x0	y0	h0	a	b
25	y' = y2 ex	0	-2	0.4	0	1.2

1. Выбрать индивидуальное задание в табл. 4-1 для решения обыкновенных дифференциальных уравнений:

• дифференциальное уравнение ;

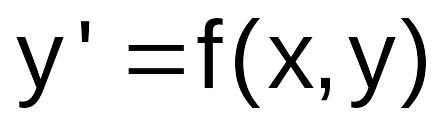• интервал [a;b] , где ищется решение дифференциального уравнения;

• начальные условия x₀, y₀;

• шаг интегрирования h_0.

2. Найти аналитическое решение заданного дифференциального уравнения, полагая его точным.

3. Создать в сценарии функцию для вычисления значений полученного решения 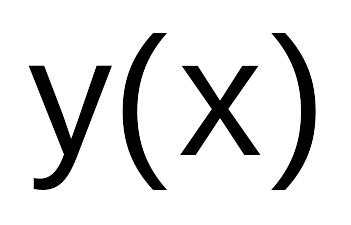на отрезке [a;b] с шагомh₀.

4. Создать в сценарии функцию для вычисления значений численное решение дифференциального уравнения методом Эйлера - 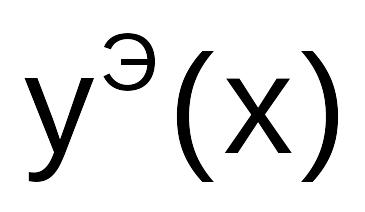в точках отрезка [a;b] с шагом h₀

5. Вычислить значения погрешностей для , ,.

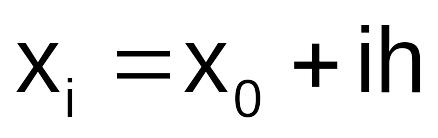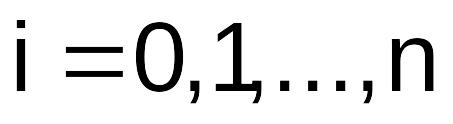6. Написать и выполнить программу, реализующую программу решения дифференциального уравнения методом Рунге-Кутта 4-го порядка y^рк(х) в точках отрезка [a;b] с шагом h₀, обеспечив с использованием метода автоматического выбора шага, точность 10^-4.

7. Вычислить значения погрешностей для , .

8. Найти решение дифференциального уравнения y^s(x)использованием функции пакета Scilab ode.

9. Проиллюстрировать решения 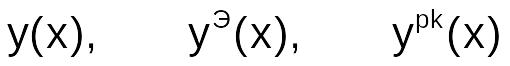в одной системе координат.

1.Точное аналитическое решение заданного дифференциального уравнения

Найдем точное аналитическое решение заданного дифференциального уравнения y(x) методом разделения переменных.

Запишем уравнение в виде 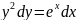  и проинтегрируем обе части равенства с учетом начальных условий.

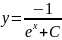
Из начальных условий найдем константу c

Таким образом, аналитическое (точное) решение дифференциального уравнения

2.Значения точного решения ОДУ

Вычислим в сценарии значения полученного решения y(x_i) на отрезке [0: 1.2] с шагом изменения аргумента h = 0.4:

xi	y(xi)
0	-2
0.4	-1.0082427
0.8	-0.5795284
1.2	-0.3545952

3.Численное решение заданного ОДУ методом Эйлера.

Найдем значения численного решения ОДУ методом Эйлера (функцию y(x)) во всех точках заданного отрезка [0; 1.2] с шагом h = 0.4_, используя математический пакет Mathcad:

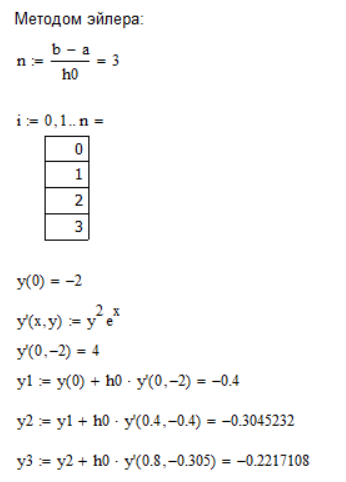
xi
0	-2
0.4	-0.4
0.8	-0.3045232
1.2	-0.2217108

4.Значения погрешностей метода Эйлера

Вычислим в Mathcad значения погрешностей

для :

xi	Ei
0	0
0.4	0.6082427
0.8	0.2750052
1.2	0.1328844

5.Численные значения ОДУ методом Рунге-Кутта 4-го порядка с точностью 10^-4

Вычислим в программе значения численного решения ОДУ с точностью 10^-4 , и получим решение в точках отрезка [0;1.2]с шагом h=0.4 методом Рунге-Кутта 4-го порядка:

import math

def f(x, y):

return y**2 * math.exp(x)

def r(x0, y0, h, m):

for j in range(1, m+1):

k1 = f(x0, y0)

k2 = f(x0 + h / 2, y0 + h * k1 / 2)

k3 = f(x0 + h / 2, y0 + h * k2 / 2)

k4 = f(x0 + h, y0 + h * k3)

y0 = y0 + (h / 6) * (k1 + 2 * k2 + 2 * k3 + k4)

x0 = x0 + h

return y0

def resh(x0, y0, h0, b, E):

print(f"x0 = {x0:.8f}; y0 = {y0:.8f}; h = {h0:.8f}; m = {1}")

n = int((b - x0) / h0 + 1)

for i in range(1, n):

h = h0

m = 1

y = r(x0, y0, h, m)

while True:

y1 = y

h = h / 2

m = 2 * m

y = r(x0, y0, h, m)

if abs(y - y1) <= E:

break

x0 = x0 + h0

y0 = y

print(f"x0 = {x0:.8f}; y0 = {y0:.8f}; h = {h:.8f}; m = {m}")

def main():

while True:

x0 = float(input("Введите значение x0:\n"))

y0 = float(input("Введите значение y0:\n"))

h0 = float(input("Введите шаг h0:\n"))

b = float(input("Введите конец отрезка b:\n"))

E = float(input("Введите погрешность E:\n"))

resh(x0, y0, h0, b, E)

choice = input("Для повторения нажмите '1'\n")

if choice != '1':

break

if __name__ == "__main__":

main()

Результат работы кода:

xi
0	-2
0.4	-1.00824444
0.8	-0.57952937
1.2	-0.35459783

Оптимальный шаг: h = 0.4

6.Значения погрешностей метода Рунге-Кутта 4-го порядка с точностью 10^-4

Вычислим значения погрешностей 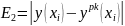, i = 0, 1, …, n:

xi	Е2
0	0
0.4	0.0031490359864162
0.8	0.003195328068308
1.2	0.0020208911939492

7.Решение дифференциального уравнения y^s(x) использованием функции математического пакета.

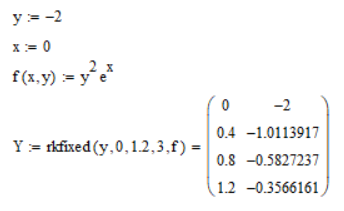
xi	ys(x)
0	-2
0.4	-1.0113917
0.8	-0.5827237
1.2	-0.3566161

8.Иллюстрированные решения y(x), y^э(x), y^pk(x) в одной системе координат

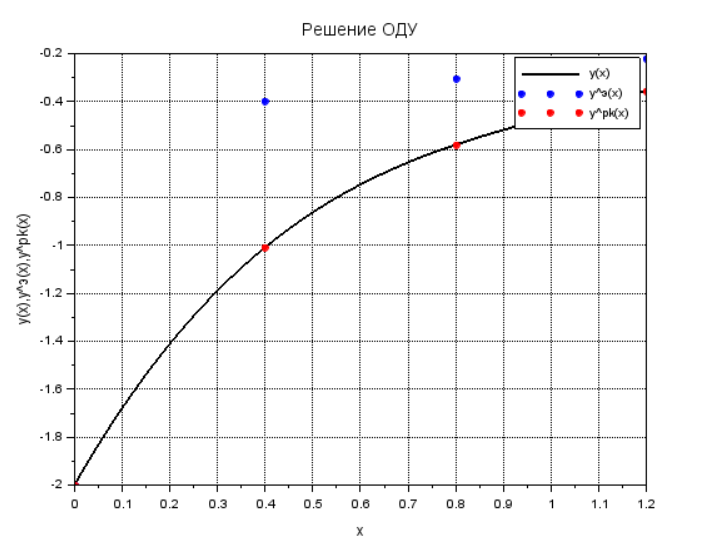
Выводы

В процессе выполнения лабораторной работы были получены численные значения ОДУ методами Эйлера и Рунге-Кутта 4 степени. Значения методов сошлись со значениями машинного расчёта, с друг с другом и с точным аналитическим решением в пределах погрешности.

xi	Точное аналитическое значение	Машинный расчёт	Метод Эйлера	Метод Рунге-Кутта 4 степени
0	-2	-2	-2	-2
0.4	-1.0082427	-1.0113917	-0.4	-1.00824444
0.8	-0.5795284	-0.5827237	-0.3045232	-0.57952937
1.2	-0.3545952	-0.3566161	-0.2217108	-0.35459783

По результатам видно, что с повышением степени метода повышается точность.