МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ СВЯЗИ И

МАССОВЫХ КОММУНИКАЦИЙ

Ордена трудового Красного Знамени федеральное государственное бюджетное

образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Кафедра «Информатика»

Лабораторная работа №3

по дисциплине «Численные методы»

на тему

«Аппроксимация функций. Метод наименьших квадратов»

Проверил:

Москва, 2024

Содержание

1.Постановка задачи 2

2.Линейная аппроксимация 3

3.Аппроксимация с помощью математического пакета scilab 5

4.Выводы 10

1.Постановка задачи

Выбрать индивидуальное задание из табл. 2-1 и табл. 2-2 для решения задачи аппроксимации методом наименьших квадратов: значения функции табл. 2-2 в узлах, указанных в табл. 2-1.

Выполнить линейную аппроксимацию: составить систему нормальных уравнений и решить её, вычислить значения аппроксимирующих функций в узловых точках и сравнить их со значениями исходной функции, Вычислить среднеквадратичную погрешность (СКО).

С использованием математического пакета получить аппроксимирующие полиномы МНК 1, 2, 3, 4, 5 степеней и соответствующие СКО. Построить графики соответствующих полиномов.

Проанализировать результаты.

Таблица 2-1:

N варианта	Функция из табл. 1-2	Номера узлов из табл. 2-2
25	f2	16,18,20,22,24,26

Таблица 2-2:

-номер узла
16	0.0	1	1
18	0.2	1,386	1,406
20	0.4	0,406	0,526
22	0.6	-0,939	-0,64
24	0.8	-1,286	-0,726
26	1.0	-0,266	0,634

2.Линейная аппроксимация

Функция:

	0.0	0.2	0.4	0.6	0.8	1.0
	1	1,406	0,526	-0,64	-0,726	0,634

i
0	0.0	1	0.0	0.0
1	0.2	1,406	0.2812	0.04
2	0.4	0,526	0.2104	0.16
3	0.6	-0,64	-0.384	0.36
4	0.8	-0,726	-0.5808	0.64
5	1.0	0,634	0.634	1.0
Σ	3.0	2.2	0.1608	2.2

Составим систему линейных уравнений для полинома первой степени:

Решим систему уравнений:

Тогда полином первой степени имеет вид:

Вычислим значения аппроксимирующих функций в узловых точках и сравним с исходными значениями, вычислим СКО:

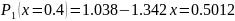
	0.0	0.2	0.4	0.6	0.8	1.0
	1	1,406	0,526	-0,64	-0,726	0,634
	-0.038	0.6364	0.0248	-0.8728	-0.6904	0.938

3.Аппроксимация с помощью математического пакета scilab

// Исходные данные

x = [0.0, 0.2, 0.4, 0.6, 0.8, 1.0];

y = [1, 1.406, 0.526, -0.64, -0.726, 0.634];

// Функция для вычисления значений полинома

function [pol] = polyval(x, a)

pol = 0;

for i = 1:1:length(a)

pol = pol + a(i) * x.^(i - 1);

end

endfunction

// Функция МНК для вычисления коэффициентов полинома заданной степени

function [a, err] = MNK(x, y, n)

// Построение матрицы дизайна A для полинома степени n

A = [];

for i = 0:n

A = [A, x'.^i];

end

// Вычисление коэффициентов полинома

a = inv(A' * A) * A' * y';

// Вычисление ошибки аппроксимации (СКО)

y_est = A * a; // Оцененные значения y

err = sqrt(sum((y' - y_est).^2) / length(y));

endfunction

// Построение графиков и вычисление СКО

clf; // Очистка графического окна

plot(x, y, 'ro'); // Изменено для исключения соединения точек линией

xgrid; // Сетка

legends = ["Data"]; // Метки

// Цикл для полиномов от 1 до 5 степени

for n = 1:5

[a, err] = MNK(x, y, n); // Вычисление коэффициентов и СКО

// Генерация точек для графика полинома

xx = linspace(min(x), max(x), 100);

yy = polyval(xx, a);

// Добавление графика полинома

plot(xx, yy, 'linestyle', '-', 'color', rand(1,3)); // Добавлено для изменения цвета каждого полинома

legends($+1) = "Degree " + string(n) + " (SKO: " + string(err) + ")";

// Вывод коэффициентов и СКО

disp("Коэффициенты полинома степени " + string(n) + ":");

disp(a);

disp("СКО для полинома степени " + string(n) + ":");

disp(err);

end

// Добавление меток к графику

legend(legends);

Результаты расчёта на ПК:

"Коэффициенты полинома степени 1:"

1.0375238

-1.3417143

"СКО для полинома степени 1:"

0.6487603

"Коэффициенты полинома степени 2:"

1.5105

-4.8890357

3.5473214

"СКО для полинома степени 2:"

0.5437042

"Коэффициенты полинома степени 3:"

1.0172222

6.3741402

-27.282540

20.553241

"СКО для полинома степени 3:"

0.0602220

"Коэффициенты полинома степени 4:"

0.9945794

8.2610450

-37.424653

37.063657

-8.2552083

"СКО для полинома степени 4:"

0.0351297

"Коэффициенты полинома степени 5:"

1.0000000

5.0881667

-10.152083

-40.406250

80.677083

-35.572917

"СКО для полинома степени 5:"

1.338D-11

Исходные данные и полиномы различных степеней, построенные по МНК:

4.Выводы

В процессе выполнения лабораторной работы выполнена аппроксимация функции методом наименьших квадратов, получили СКО, полиномы 1,2,3,4,5 степеней, получили их графики.

Результаты расчёта с помощью scilab и результаты ручного расчёта показали, что с повышением степени аппроксимационного полинома значительно возрастает точность аппроксимации.