СВЧкурсач

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени Федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики» (МТУСИ)

Кафедра: ТЭДиА

Дисциплина: УСВЧиЛП

Курсовая работа

Задача №1

«Электромагнитное поле в прямоугольном волноводе»

Бригада №

Вариант №

Выполнил: студент группы

Проверила:

Москва 2024

Задача №1

«ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ В ПРЯМОУГОЛЬНОМ ВОЛНОВОДЕ»

Бригада № 4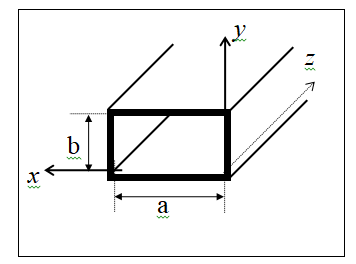

В полой трубе прямоугольного сечения (см. рисунок) с идеально проводящими стенками создано монохроматическое электромагнитное поле. Труба заполнена однородной изотропной средой без потерь, абсолютные диэлектрическая и магнитная проницаемости равны ε_а и μ_а соответственно. Известно, что комплексная амплитуда вектора равна:

, где

f - частота колебаний; λ = C / f - длина волны, свободно распространяющейся в однородной среде с параметрами ε_а и μ_а; - скорость света в среде

ЗАДАНИЕ

1. Используя уравнения Максвелла, найти комплексные амплитуды всех остальных, не заданных в условии задачи, составляющих векторов и .

2. Определить диапазон частот, в котором параметр β - действительное число, т.е. рассматриваемое поле - бегущая волна.

3. Записать выражения для мгновенных значений всех составляющих векторов полей. Рассчитать и построить графики зависимостей мгновенных значений составляющих полей от координаты z (при х=а/3 и у=b/3) в два момента времени t1=0 и t2=T/4 в интервале 0 ≤ z ≤ 2Λ, где Λ – длина волны в волноводе на частоте f2. Задания этого пункта выполняется для частот: f1 и f2.

4. Проверить выполнение граничных условий для касательных составляющих вектора и нормальной составляющей вектора на всех стенках трубы.

5. Определить максимальные значения плотностей продольного и поперечного поверхностных токов на всех стенках волновода на частоте f2.

6. Вычислить средний за период поток энергии через поперечное сечение трубы.

7. Определить фазовую скорость V_ф и скорость распространения энергии V_э рассматриваемой волны. Рассчитать и построить графики зависимостей V_ф и V_э от частоты.

8. Нарисовать структуру силовых линий электрического и магнитного полей волны в волноводе. Изобразить структуру силовых линий плотности поверхностного тока проводимости, протекающего по стенкам волновода.

Таблица 1 – исходные данные

№ вар.	E0 B/м	εr	μr	a см	b см	f1 ГГц	f2 ГГц
1	80	4	1	4	2	2,0	5,5
2	100	2	1	5	3	2,5	6

ВЫПОЛНЕНИЕ РАБОТЫ

1. Используя уравнения Максвелла, найти комплексные амплитуды всех остальных, не заданных в условии задачи, составляющих векторов и .

Чтобы получить комплексные амплитуды вектора , воспользуемся формулой второго уравнения Максвелла:

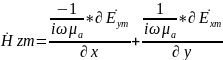
Продифференцируем и получим:

В результате анализа показано, что вектор Е имеет все три составляющие, то есть Hz не равняется 0 а Ez по условию равняется нулю значит по классификации это волны H индекс m по заданию равен 1 и n равен 1 значит у нас волна H11.

2. Определить диапазон частот, в котором рассматриваемое поле представляет собой волну, бегущую вдоль оси .

для того, чтобы β было действительным числом, необходимо, чтобы значение под корнем было больше или равно нулю.

м

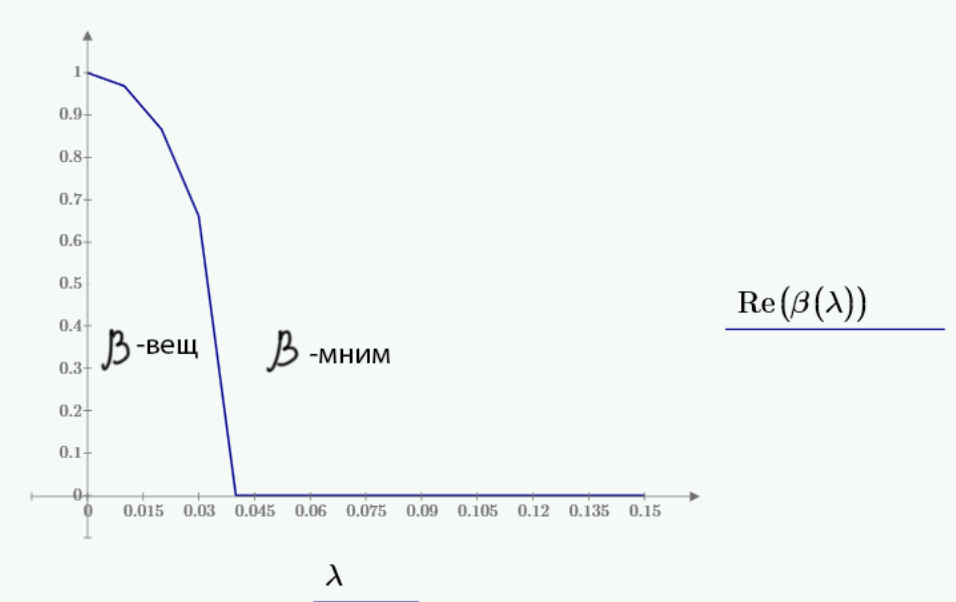
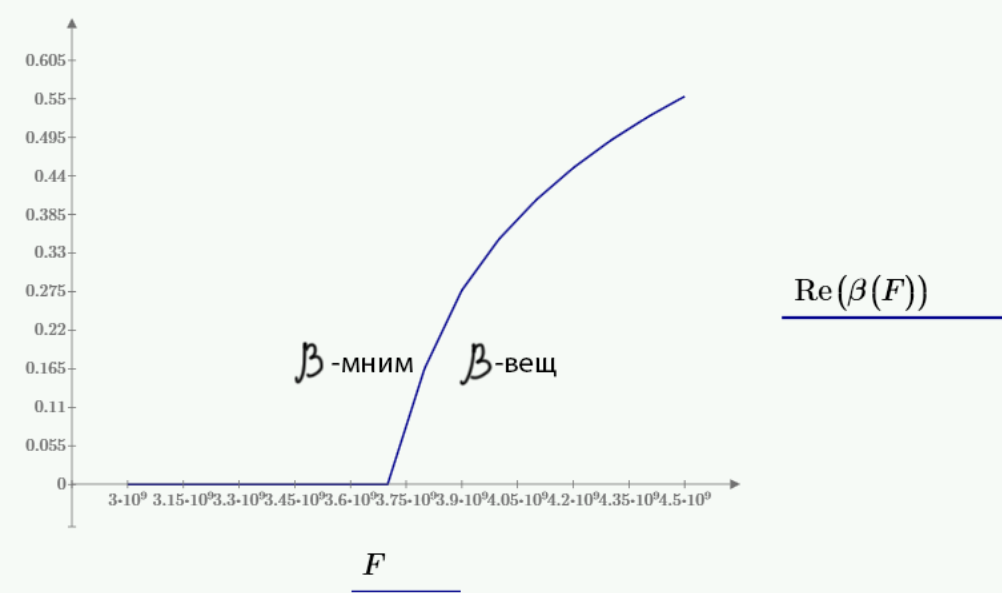
Рис. 1 – Графики зависимости реальной части параметра β от частоты и длины волны

3. Записать выражения для мгновенных значений всех составляющих векторов полей. Рассчитать и построить графики зависимостей мгновенных значений составляющих полей от координаты (при ) в два момента времени и в интервале , где – длина волны в волноводе на частоте .

м

м

м

Для частоты f1 = 2 ГГц:

рад/с

с

с ; с

м

Выражения для мгновенных значений составляющих векторов полей:

Рис. 2 – График зависимости мгновенного значения составляющей Hx от значения координаты z при частоте f1, при временах t1 и t2

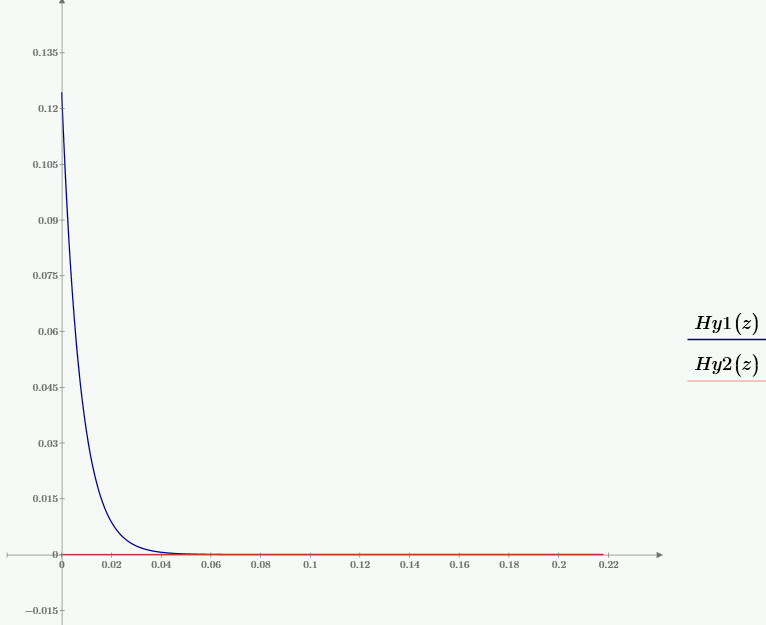
Рис. 3 – График зависимости мгновенного значения составляющей Hy от значения координаты z при частоте f1, при временах t1 и t2

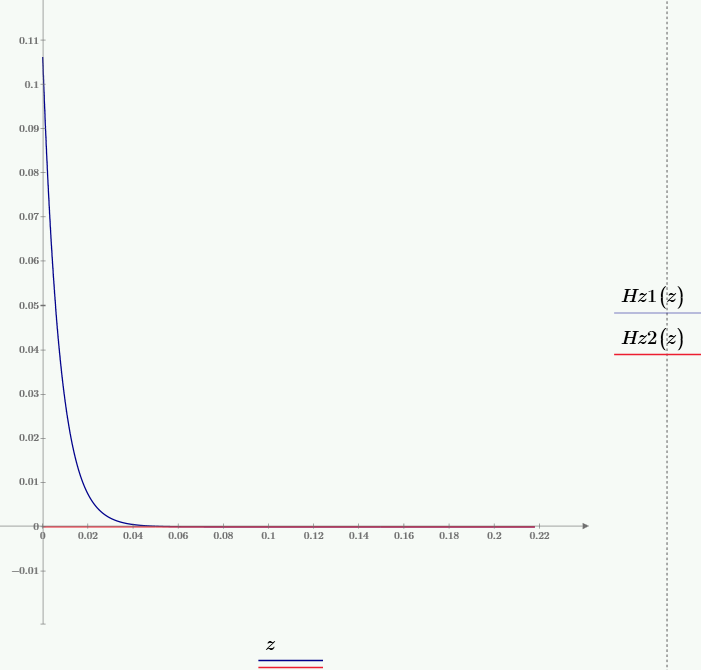
Рис. 4 – График зависимости мгновенного значения составляющей Hz от значения координаты z при частоте f1, при временах t1 и t2

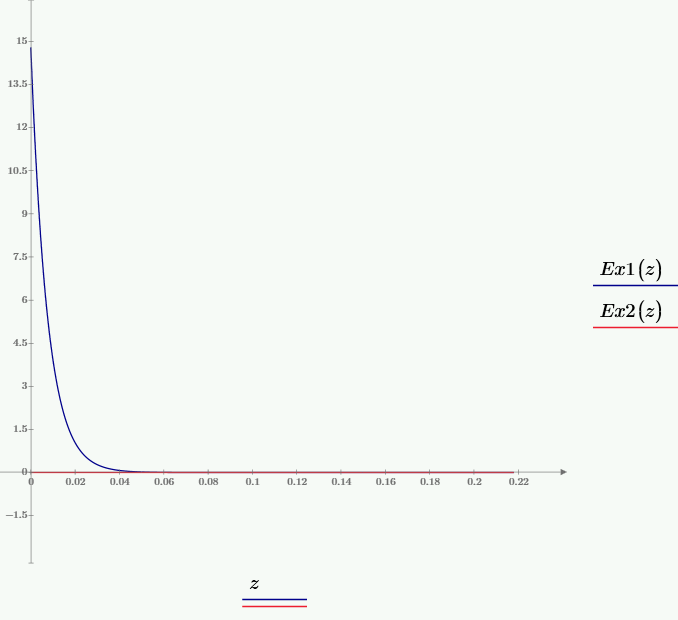
Рис. 5 – График зависимости мгновенного значения составляющей Ex от значения координаты z при частоте f1, при временах t1 и t2

Рис. 6 – График зависимости мгновенного значения составляющей Ey от значения координаты z при частоте f1, при временах t1 и t2

Для частоты f2 = 5.5 ГГц:

рад/с

с

с

с

м

Выражения для мгновенных значений составляющих векторов полей:

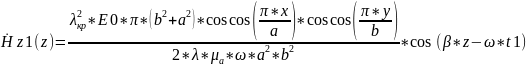
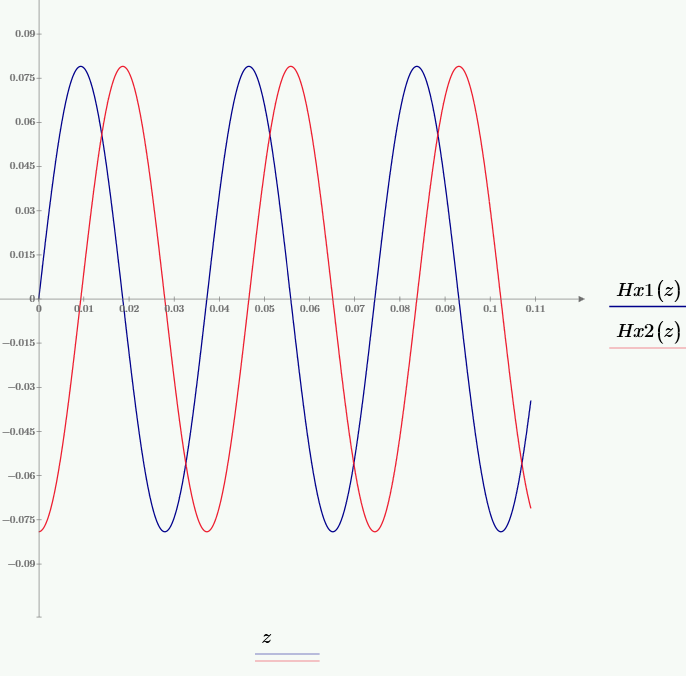
Рис. 8 – График зависимости мгновенного значения составляющей Hx от значения координаты z при частоте f2, при временах t1 и t2

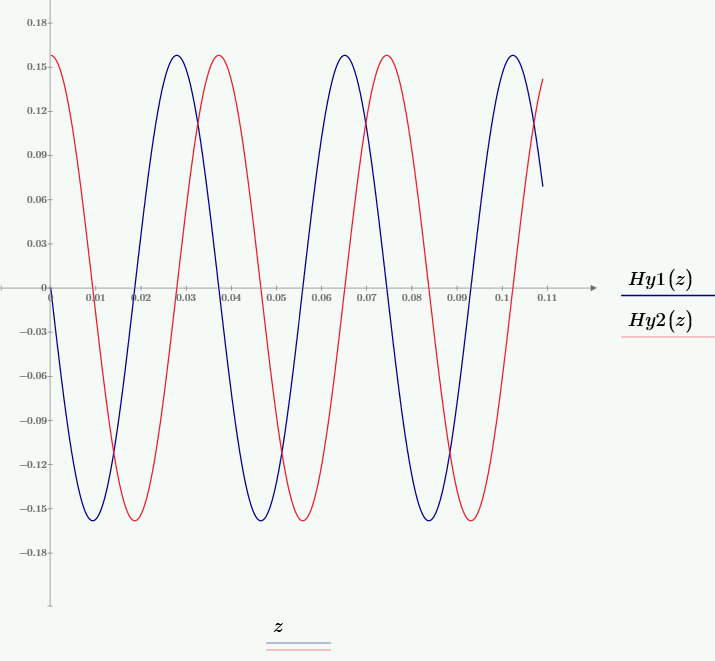
Рис. 9 – График зависимости мгновенного значения составляющей Hy от значения координаты z при частоте f2, при временах t1 и t2

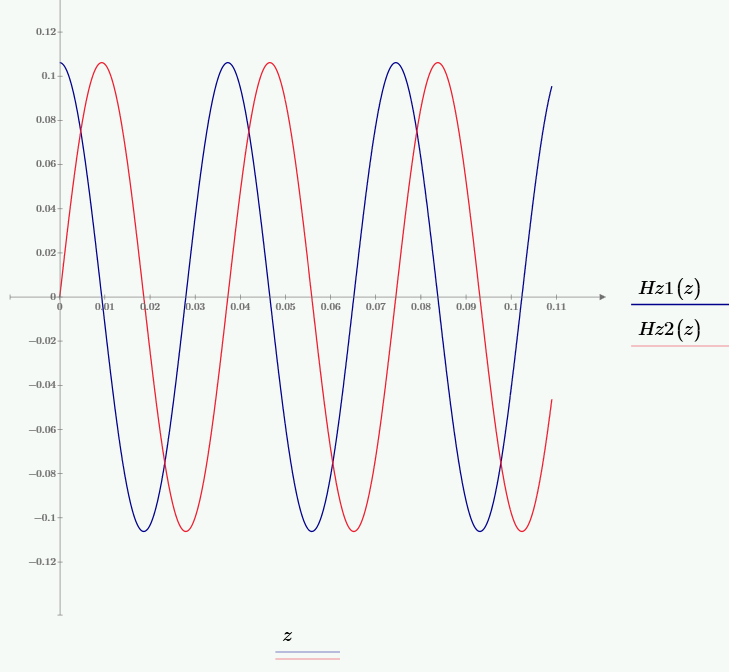
Рис. 10 – График зависимости мгновенного значения составляющей Hz от значения координаты z при частоте f2, при временах t1 и t2 (поправить)

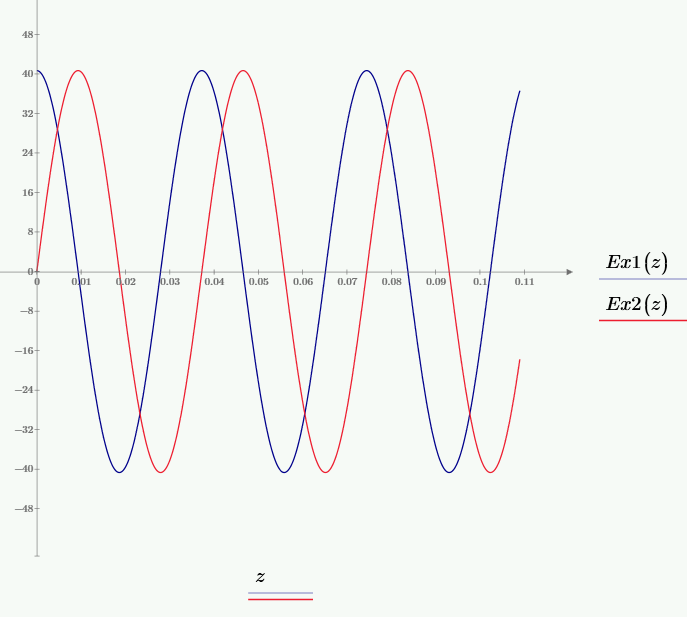
Рис. 11 – График зависимости мгновенного значения составляющей Ex от значения координаты z при частоте f2, при временах t1 и t2

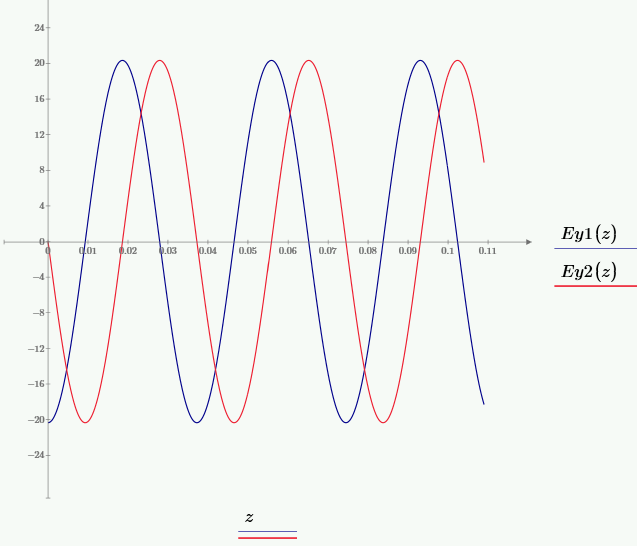
Рис. 12 – График зависимости мгновенного значения составляющей Ey от значения координаты z при частоте f2, при временах t1 и t2

4. Проверить выполнение граничных условий на стенках волновода (при x=0, a и y=0, b).

Граничные условия гласят, что касательные составляющие вектора и нормальная составляющая вектора будут равны 0 на границе сред (Границы сред: y = 0, b и x = 0, a)

Нижняя стенка:

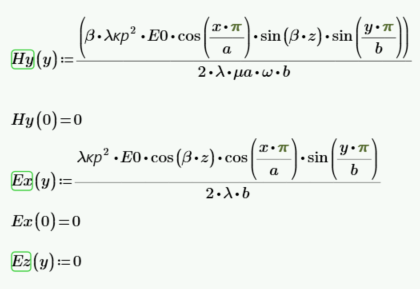
Верхняя стенка:

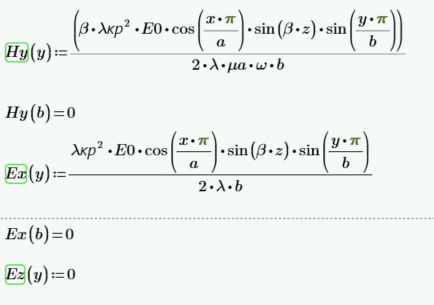
Правая стенка:

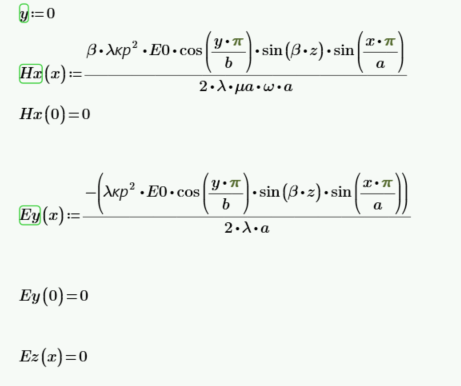
Левая стенка:

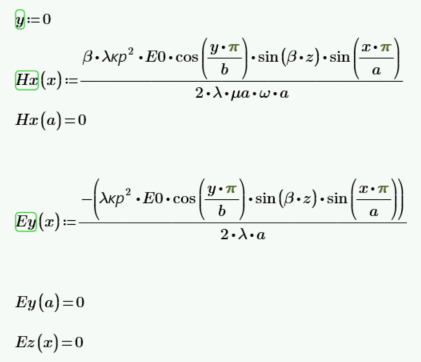
Нижняя и верхняя стенки:

H_n = H_y – нормальная

E_τ = E_x, E_z – касательные

Правая и левая стенки:

H_n = H_x – нормальная

E_τ = E_y, E_z – касательные

5. Определить максимальные значения плотностей продольного и поперечного поверхностных токов на всех стенках волновода на частоте f₂.

Верхняя стенка:

Максимальное значение – при модуле синуса и косинуса равном единице:

при x ,

при y ,

Максимальные значения x – при модуле косинуса равном единице:

при x ,

при y ,

Нижняя стенка:

Максимальное значение – при модуле синуса и косинуса равном единице:

при x ,

при y ,

Максимальные значения x – при модуле косинуса равном единице:

при x ,

при y ,

Правая стенка:

Максимальное значение – при модуле синуса и косинуса равном единице:

при x ,

при y ,

Максимальные значения y – при модуле косинуса равном единице:

при x ,

при y ,

Левая стенка:

Максимальное значение – при модуле синуса и косинуса равном единице:

при x ,

при y ,

Максимальные значения y – при модуле косинуса равном единице:

при x ,

при y ,

6. Вычислить средний за период поток энергии через поперечное сечение волновода на частоте f₂.

Выделим реальную часть:

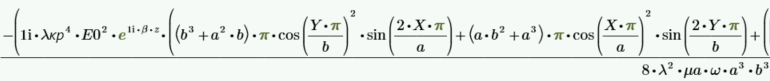
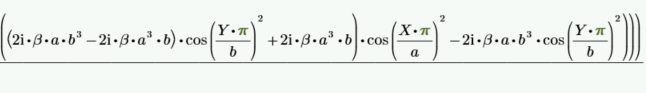
т

7. Определить фазовую скорость V_ф и скорость распространения энергии волны V₀ на частоте f₂. Рассчитать и построить графики зависимости этих скоростей от частоты.

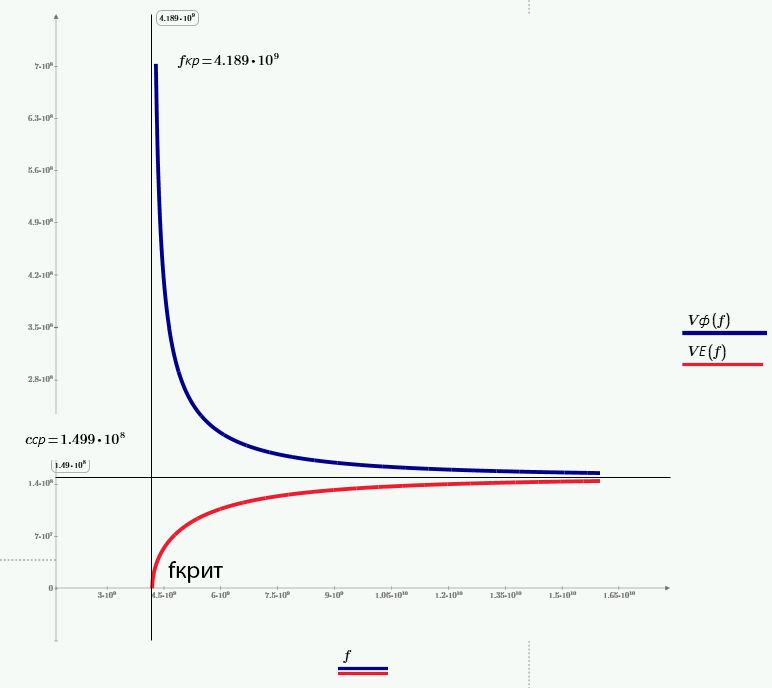
Рис. 13 – График зависимости фазовой скорости и скорости распространения энергии от частоты

8. Нарисовать структуру векторных линий полей и эпюры токов на стенках волновода.

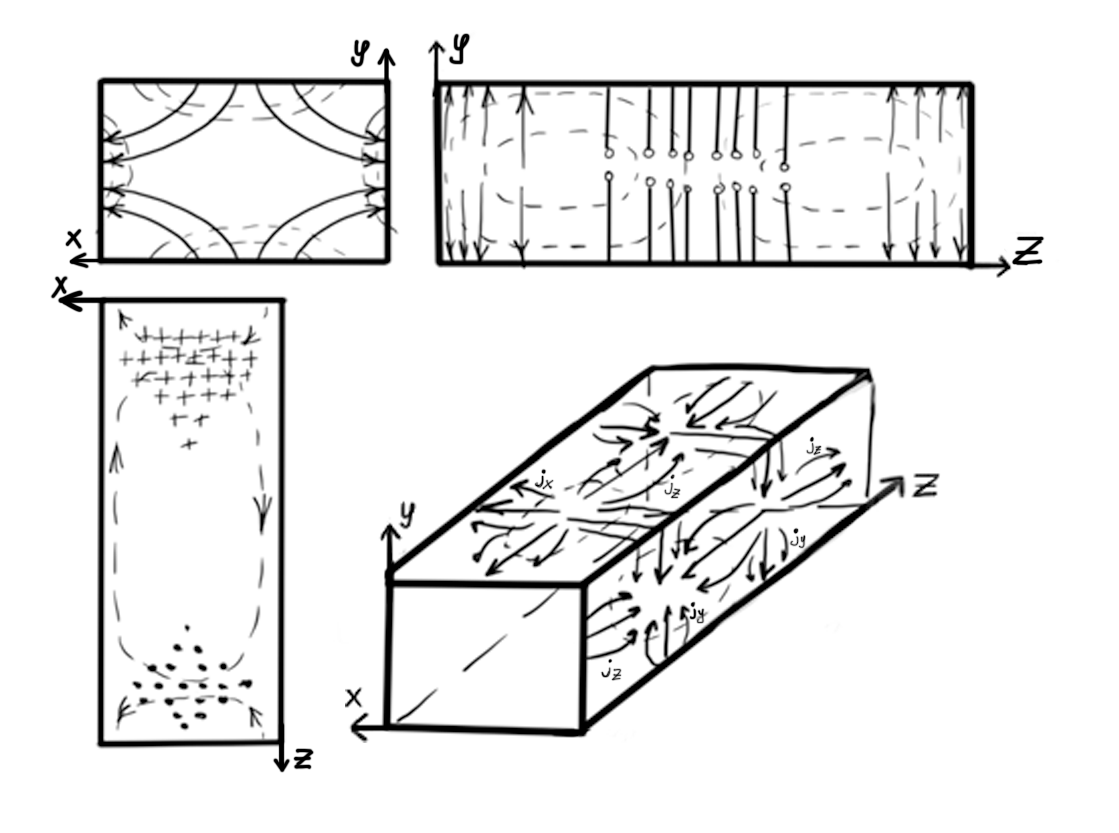
Рис. 14 – Рисунок структуры силовых линий электрического и магнитного полей волны в волноводе и структуры силовых линий плотности поверхностного тока проводимости, протекающего по стенкам волновода для волны H₁₁

Ток определяется составляющей – составляющей , – составляющей .

Вывод:

В ходе выполнения курсовой работы было проведено исследование поведения электромагнитной волны типа H11 в прямоугольном волноводе. В процессе были определены её основные характеристики, включая критическую частоту, критическую длину волны, фазовую и групповые скорости распространения. Было проанализировано изменение мгновенных значений полей вдоль оси z при частотах, как ниже, так и выше критической. Особое внимание уделялось проверке выполнения граничных условий и изучению распределения поверхностных токов на стенках волновода. Были также рассчитаны средние значения потока энергии через поперечное сечение волновода за период. На основании анализа типа волны и характеристик её векторных составляющих были построены графические структуры силовых линий электрического и магнитного полей. Эти результаты помогли лучше понять поведение электромагнитных полей внутри волновода и подтвердили теоретические предположения о его характеристиках.

Список литературы

1. Седов В.М., Гайнутдинов Т.А., Электромагнитные поля и волны. 2-е изд., перераб. и доп.. учебное пособие для студентов вузов 2023г., 282стр.

2. Седов В. М., Гайнутдинов Т. А., Электромагнитные поля и волны Конспект лекций 2000г., 49стр.