МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ СВЯЗИ И

МАССОВЫХ КОММУНИКАЦИЙ

Ордена трудового Красного Знамени федеральное государственное бюджетное

образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Кафедра «Информатика»

Лабораторная работа №2

по дисциплине «Численные методы»

на тему

«Интерполяция функций»

Проверил:

Москва, 2024

Содержание

1. Задание 2

2. Выполнение 3

Индивидуальное задание 4

Интерполяция с использованием полинома Ньютона 4

Ручной расчет по 1–й формуле Ньютона. 4

Произведем расчёты при помощи программы MathCad. 6

Интерполяция с использованием полинома Лагранжа 8

Ручной расчёт по формуле Лагранжа 8

Произведем расчёты при помощи программы MathCad. 11

3. Вывод 11

1. Задание

2. Выбрать индивидуальное задание из табл. 1-1:

• точку интерполяции x=a для интерполяции полиномом Ньютона;

• точку интерполяции x=b для интерполяции полиномом Лагранжа.

3. Выполнить вручную интерполяцию в заданной точке x=a с использованием полинома Ньютона 1–й, 2–й и 3–й степени:

• выбрать из таблицы 1–2 с интерполируемой функцией четыре подходящих узла. Перенумеровать узлы и занести перенумерованные узлы в таблицу.

• заполнить таблицу конечных разностей (для интерполяционной формулы Ньютона);

• записать интерполяционные формулы для 1, 2 и 3-ей степени полинома;

• выполнить расчеты по интерполяционным формулам для каждой степени полинома;

• занести полученные результаты в таблицу;

• вычислить оценки погрешности в точке и для полиномов различных степеней и занести их в таблицу.

4. Выполнить вручную интерполяцию в заданной точке x=b с использованием полинома Лагранжа 1–й, 2–й и 3–й степени:

• выбрать из таблицы 2–2 с интерполируемой функцией четыре подходящих узла. Перенумеровать узлы и занести перенумерованные узлы в таблицу;

• записать интерполяционные формулы для 1, 2 и 3-ей степени полинома;

• выполнить расчеты по интерполяционным формулам для каждой степени полинома;

• занести полученные результаты в таблицу;

• вычислить оценки погрешности в точке b для полиномов различных степеней и занести их в таблицу.

5. Решить задачу интерполяции в точке с точностью 0.0001 на компьютере.

6. Объяснить полученные результаты и сделать выводы.

2. Выполнение

Индивидуальное задание

№ варианта	Полином Ньютона x=a	Полином Лагранжа x=b
25	0.42	1.12

Интерполяция с использованием полинома Ньютона

Для ручной интерполяции в точке x = a = 0.42с использованием полинома Ньютона выбираем 4 узла из таблицы 1–2 так, чтобы точка a = 0.42 оказалась внутри таблицы между узлами с номерами 0 и 1:

k	0	1	2	3
xk	0.40	0.45	0.50	0.55
yk	-3.6320	-3.4890	-3.3250	-3.1385

Ручной расчет по 1–й формуле Ньютона.

Заполним таблицу конечных разностей:

x	y	Δy	Δy2	Δy3
0.40	-3.6320	0.1430	0,0210	0.0015
0.45	-3.4890	0.1640	0.0225	0.0015
0.50	-3.3250	0.1865	0.0240
0.55	-3.1385	0.2105

Запишем 1–ю интерполяционную формулу Ньютона

Произведём ручной расчёт:

Полиномы Ньютона в явном виде для точки x = 0.42:

(Полином Ньютона первой степени)

= 3.57732 (Полином Ньютона второй степени)

= 3.577224 (Полином Ньютона третьей степени)

Произведём оценку погрешности:

R₁=|P₂(x)-P₁(x)|=0,0025

R₂=|P₃(x)-P₂(x)|=0,0001

Результат ручного расчёта:

Степень многочлена k	Pk(x)	Погрешность
1		0.0025
2	3.57732	0.0001
3	3.577224	–

Проверка правильности построения полинома Ньютона:

Для узла 0.40:

= 3.632

= 3.632

Для узла 0.45:

= 3.489

= 3.489

Для узла 0.50:

= 3.325

= 3.325

Для узла 0.55:

= 3.14

= 3.1385

Полином	Точка 0.40	Точка 0.45	Точка 0.50	Точка 0.55
Исходный	0		-3.3250	3.1385
P1	0
P2	0		3.3250	3.1400
P3	0		3.3250	3.1385

Результаты интерполяции полиномом совпадают с реальными значениями в рамках погрешности, полиномы построены правильно.

Произведем расчёты при помощи программы MathCad.

Представим результаты в виде таблиц.

Таблица конечных разностей:

x	y	Δy	Δy2	Δy3
0.40	-3.6320	0.1430	0,0210	0.0015
0.45	-3.4890	0.1640	0.0225
0.50	-3.3250	0.1865
0.55	-3.1385

Значения полиномов Ньютона и оценка погрешностей с учётом округления результатов:

Степень многочлена k	Pk(x)	Погрешность
1		0.002520
2	-3.57732	0.000096
3	-3.577224	–

Интерполяция с использованием полинома Лагранжа

Для ручной интерполяции в точке x = b = 1.12 по формуле Лагранжа выбираем из таблицы 1–2 4 узла так, чтобы точка b = 1.12 оказалась внутри таблицы и узлы были наиболее близкими к этой точке.

k	0	1	2	3
xk	1.10	1.15	1.05	1.20
yk	0.8270	1.4005	0.2940	2.0160

Ручной расчёт по формуле Лагранжа

Запишем интерполяционные формулы полиномов Лагранжа

Произведём ручной расчёт:

Полиномы Лагранжа в явном виде для точки x = 1.12:

(Полином Лагранжа первой степени)

(Полином Лагранжа второй степени)

(Полином Лагранжа третьей степени)

Произведём оценку погрешности:

R₁=|L₂(x)-L₁(x)|=0,0025

R₂=|L₃(x)-L₂(x)|=0,0001

Результат ручного расчёта:

Степень многочлена k	Pk(x)	Погрешность
1		0.0049
2		0.0001
3		–

Проверка правильности построения полинома Лагранжа:

Для узла 1.10:

Для узла 1.15:

Для узла 1.05:

Для узла 1.20:

Полином	Точка 1.10	Точка 1.15	Точка 1.05	Точка 1.20
Исходный	0.8270	1.4005	0.2940	2.0160
L1	0.8270	1.4005		2.0160
L2	0.8270	1.4005	0.2940
L3	0.8270	1.4005	0.2940	2.0160

Результаты интерполяции полиномом совпадают с реальными значениями в рамках погрешности, полиномы построены правильно.

Произведем расчёты при помощи программы MathCad.

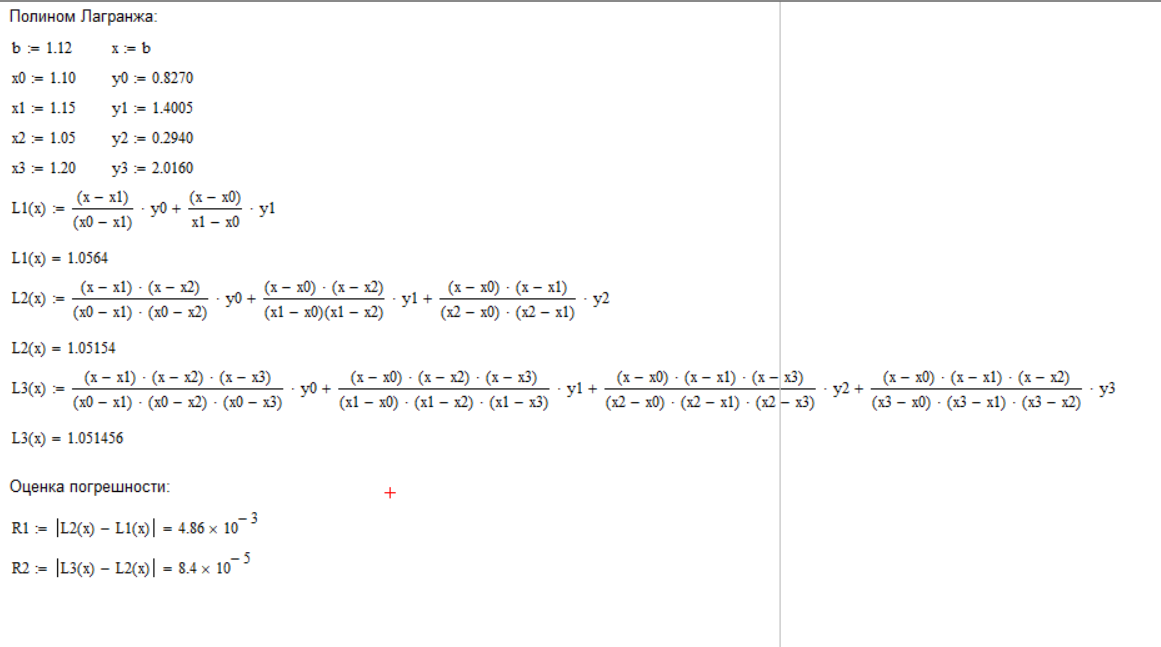
Представим результаты в виде таблиц:

Значения полиномов Лагранжа и оценка погрешностей с учётом округления результатов:

Степень многочлена k	Lk(x)	Оценка погрешности
1	1.056400	0.004860
2	1.051540	0.000084
3	1.051456

2. Вывод

Были проведены расчёты значений полиномов Ньютона и Лагранжа и оценок погрешностей.

После расчёта полинома Ньютона второй степени оценка погрешности составила 0.000096. Можно утверждать, что после 3-х итераций оценка погрешности не превышает 0.00096.

После расчёта полинома Лагранжа второй степени оценка погрешности составила 0.000084. Можно утверждать, что после 3-х итераций оценка погрешности не превышает 0.000084.