Ордена Трудового Красного Знамени Федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики» (МТУСИ)

Предмет:

Теоретические Основы Электротехники.

Лабораторная работа №33 по теме:

«Исследование активных интегрирующих и дифференцирующих цепей»

Проверила:

Степанова А. Г.

Москва 2023

Цель работы:

С помощью машинного эксперимента получить форму напряжения на выходе активных интегрирующих и дифференцирующих цепей при различных формах напряжения на входе. Сравнить полученные характеристики с помощью программы Micro-Cap, с аналогичными характеристиками, полученными расчетным путём.

Формулы:

u₁(t)=U_msin(2пft), - синусоидальное входное напряжение

где U_m=1В – амплитуда входного напряжения;

f=2 кГц – частота входного напряжения;

tϵ[0;1] мс – время.

u₁(t)- прямоугольное входное напряжение

Для интегрирующей цепи:

u₂(t)=K_{1 ,}

u₂(t) – выходное напряжение

K₁ – коэффициент пропорциональности

Для активной интегрирующей цепи:

U₂=(-1/ (jwRC)) U₁

Для дифференцирующей цепи:

u₂(t)= K₂(du₁/dt),

где

u₂(t) – выходное напряжение;

K₂ – коэффициент пропорциональности

Для активной дифференцирующей цепи:

U₂=-jwRC U₁

Предварительный расчет:

1)Графики активной интегрирующей цепи при K=10 (нижний график – вход, верхний – выход):

При синусоидальном входном напряжении

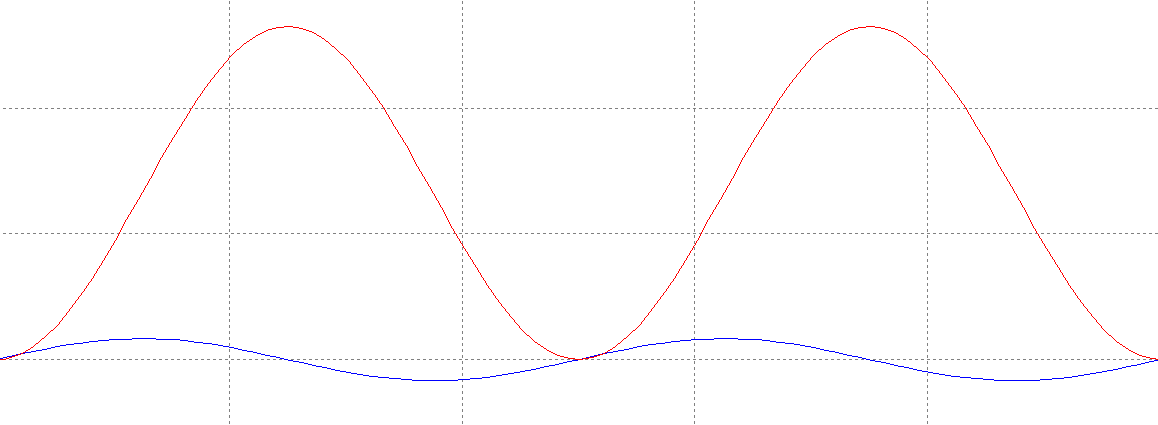
При прямоугольной форме входного напряжения

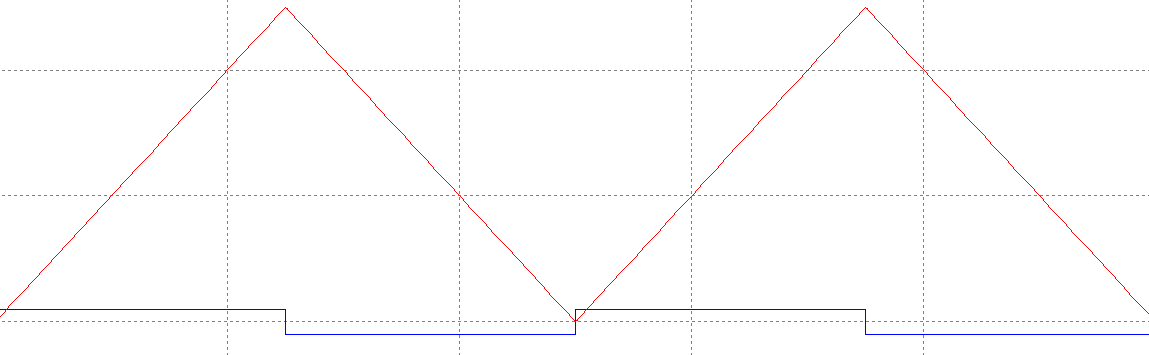
При треугольной форме входного напряжения

(средний график – вход, верхний – выход):

Расчет комплексно-передаточной функции интегрирующей цепи:

2)C = 100 нФ, R = 1 кОм, f = 2 кГц

Расчет комплексно-передаточной функции интегрирующей цепи

H=U₂/U₁= (I*Z₂)/I*(Z₁+Z₂)=Z₁/(Z₁+Z₁)

Z₁=R

Z₂=1/iωC

H=(1/iωC )/(R+1/ iωC)

ω=2πf

H=(1/i2πfC )/(R+1/i2πfC)

= 0,3877 – i 0,4872

3)Графики входных и выходных сигналов для дифференцирующей цепи при K=6 (средний график – вход, верхний – выход):

При синусоидальном входном напряжении

При прямоугольной форме входного напряжения

(верхний график – вход, прямая – выход):

При треугольной форме входного напряжения

(верхний график(М) – вход, нижний график – выход):

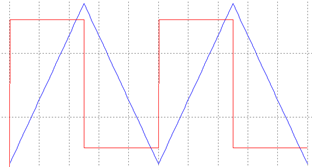
4)Расчет комплексно-передаточной функции дифференцирующей цепи:

C = 100 нФ, R = 1 кОм, f = 2 кГц

Расчет комплексно-передаточной функции дифференцирующей цепи

H=U₂/U₁= (I*Z₂)/I*(Z₁+Z₂)=Z₁/(Z₁+Z₁)

Z₂=R

Z₁=1/iωC

H=R/(R+1/ iωC)

ω=2πf

H=R/(R+1/i2πfC)

= 0,6123 + i 0,4872

Эксперимент:

Интегрирующая цепь при синусоидальном воздействии

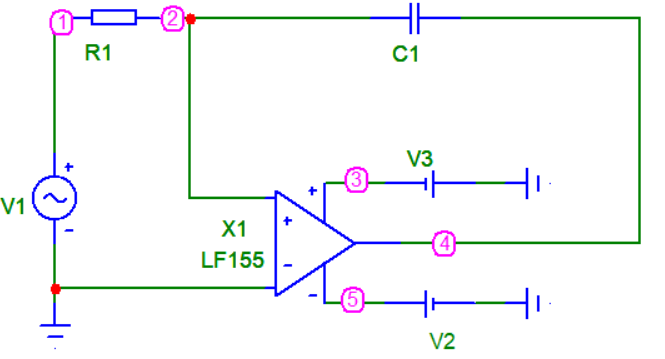
Графики входного и выходного сигнала интегрирующей цепи синусоидального воздействия (верхний график-вход, нижний график-выход)

Вывод: Из графиков мы видим, что выходной сигнал интегрирующей активной цепи представляет собой проинтегрированный входной сигнал, то есть, синусоида заменилась косинусоидой.

Интегрирующая цепь при прямоугольном воздействии

Графики входного и выходного сигнала интегрирующей цепи при прямоугольном воздействии (верхний график-вход, нижний график-выход)

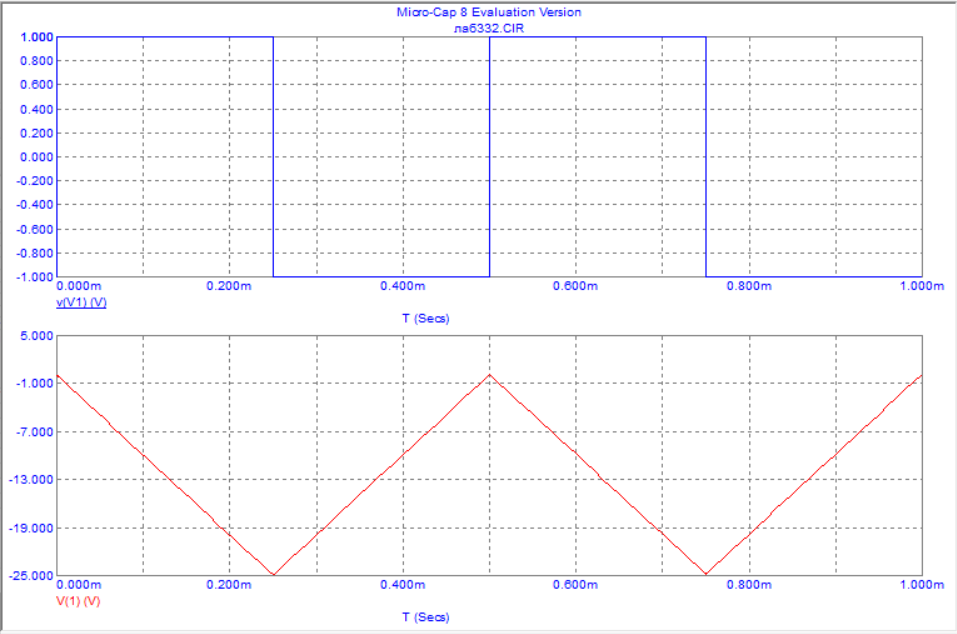
Вывод: Из графиков мы видим, что выходной сигнал интегрирующей активной цепи при прямоугольном воздействии представляет собой сигнал пилообразной формы, то есть, проинтегрированную прямоугольность последовательность импульсов.

Графики входного и выходного сигнала интегрирующей цепи при треугольном воздействии (верхний график-вход, нижний график-выход)

Вывод: Из графиков мы видим, что выходной сигнал интегрирующей активной цепи при треугольном воздействии представляет собой проинтегрированную пилообразную последовательность , то есть , синусоиду.

Графики входного и выходного сигнала дифференцирующей цепи при синусоидальном воздействии (верхний график-вход, нижний график-выход)

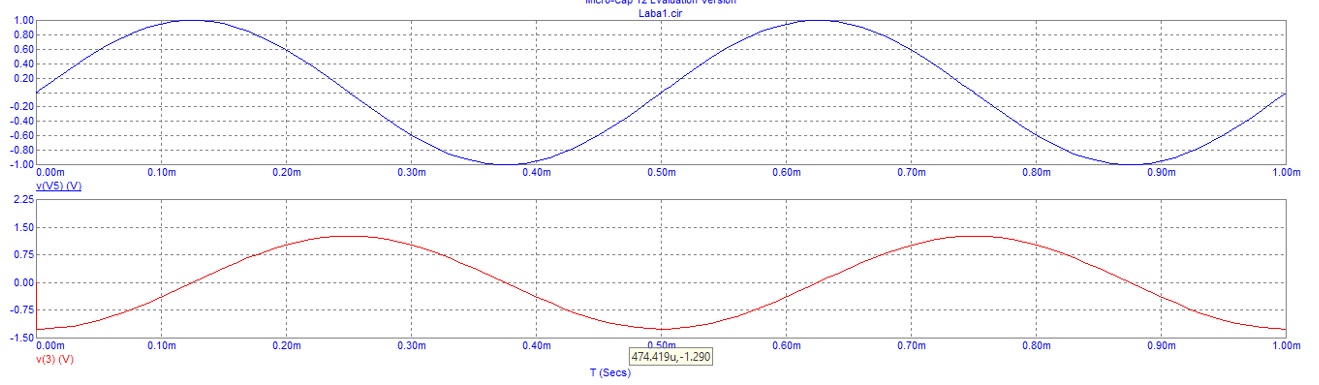
Вывод: Из графика мы видим, что выходной сигнал дифференцирующей активной цепи при синусоидальном воздействии представляет собой продифференцированную синусоиду, то есть, косинусоиду.

Графики входного и выходного сигнала дифференцирующей цепи при прямоугольном воздействии (верхний график-вход, нижний график-выход)

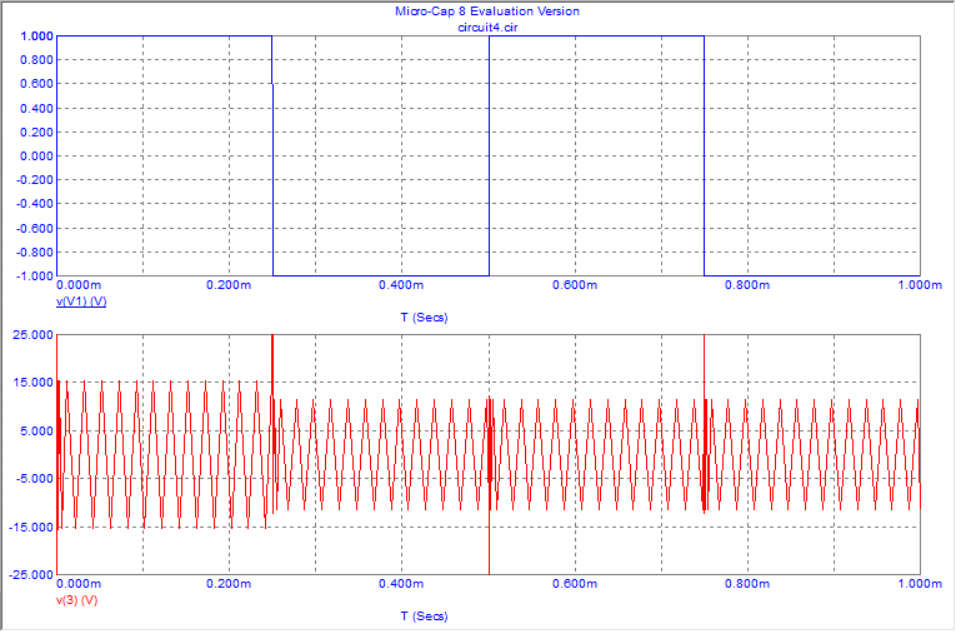
Вывод: Из графика мы видим, что выходной сигнал дифференцирующей активной цепи при прямоугольном воздействии представляет собой повторяющуюся последовательность продифференцированных прямоугольных импульсов.

Графики входного и выходного сигнала дифференцирующей цепи при треугольном воздействии (верхний график-вход, нижний график-выход)

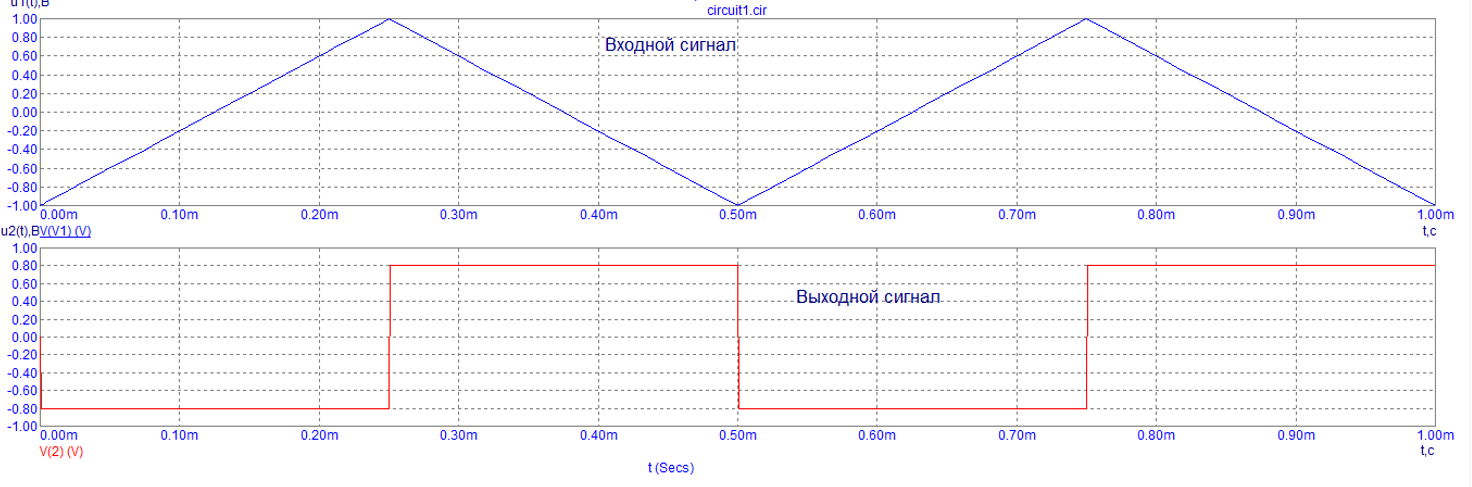
Вывод: Из графика мы видим, что выходной сигнал дифференцирующей пассивной цепи при треугольном воздействии представляет собой повторяющуюся последовательность прямоугольных импульсов с небольшими искажениями, которые являются производной от пилообразной последовательности на входе.

Вывод:

С помощью машинного эксперимента получил форму напряжения на выходе активных интегрирующих и дифференцирующих цепей при различных формах напряжения на входе.

Контрольные Вопросы:

1. Какие цепи называются интегрирующими? Приведите пример.

Ответ: Интегрирующие цепи – такие цепи, у которых выходное напряжение пропорционально интегралу входного напряжения.

Пример: Пассивная RC-цепь.

2. Какие цепи называются дифферинцирующими? Приведите пример.

Ответ: Дифференцирующие цепи – такие цепи, у которых выходной сигнал прямопропорционален производной входного сигнала.

Пример: Пассивная CR-цепь

3. В каких случаях применяются интегрирующие цепи?

Ответ: Интегрирующие цепи применяют для выполнения операций интегрирования в аналоговых вычислительных устройствах.

4. В каких случаях применяются дифференцирующие цепи?

Ответ: Дифференцирующие цепи применяют тогда, когда требуется преобразовать входное напряжение в сигнал ,изменяющийся по закону производной входного напряжения.

5. Нарисуйте схему интегратора на ОУ и выведите его передаточную функцию H.

Ответ:

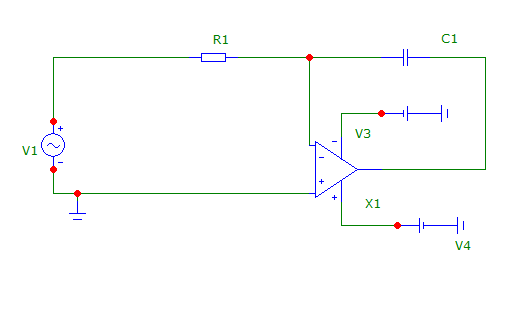
H=U₂/U₁= (I*Z₂)/I*(Z₁+Z₂)=Z₁/(Z₁+Z₁)

Z₁=R

Z2= Jwc/R

H=( Jwc/R)/(R+ Jwc/R)

ω=2πf

H=( J2πfc/R )/(R+ J2πfc/R)

6. Нарисуйте схему дифференциатора на ОУ и выведите его передаточную функцию H.

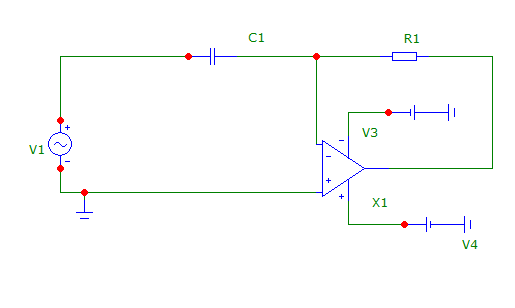
H=U₂/U₁= (I*Z₂)/I*(Z₁+Z₂)=Z₁/(Z₁+Z₁)

Z₂=R

Z₁= R/jwc

H=R/(R+ R/jwc)

ω=2πf

H=R/(R+ R/j2πf c)