лабы / лаба№5потоэ

Ордена Трудового Красного Знамени Федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики» (МТУСИ)

Предмет:

Теоретические Основы Электротехники.

Лабораторная работа №17 по теме:

«Исследование на ЭВМ резонансных явлений в пассивном параллельном колебательном контуре»

Проверил:

Волков А. С.

Москва 2023

Цель работы:

С помощью программы Micro-Cap получить входные и передаточные характеристики одиночного параллельного колебательного контура при различных добротностях.

Формулы:

lm(Y_BX)=0

Y_BX= +j(wC-

lm(Y_BX)=w_pC- =0 – резонансная частота контура

w_p= ; w_p=2пf_p; f_p=

p= – характеристическое сопротивление

Q= = – добротность

Нижняя граничная частота:

w₁=-

f₁₌

Верхняя граничная частота:

w₂=-

f₂₌

П=f2-f1 – абсолютная полоса пропускания

Z_BX= – комплексное входное сопротивление

Z_(w)= – модуль входного сопротивления

Ф(w)= – фаза входного сопротивления

Комплексные токи:

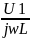I= , I_R= , I_L= , I_C=

Q= – добротность последовательного контура

R= – для контура первого типа

W_p=

f_p1=

Z_BX= – комплексное входное сопротивление

Z(f_p1)=RQ² – модуль входного сопротивления при резонансе

Таблица №1:

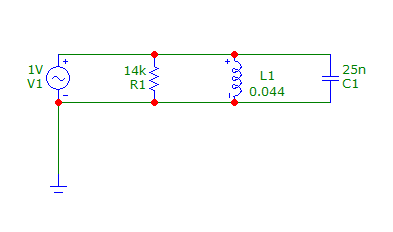
По предварительному расчету R=14 кОм, fp=5кГц, С=25 нФ, L=0,041 Гн						Получено экспериментально
ρ, кОм	Q	f1, кГц	f2, кГц	П, кГц	Z(fp), Ом		fp, кГц	Z(fp), Ом	f1, кГц	f2, кГц	П, кГц	Q
1,281	10,9	4,8	5,2	0,4	13907		5	13910	4,6	5	0,46	10,6

f_p=

L=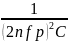 =0,041 Гн

p= =1,281

Q= =10,9

w₁=- =29838

f_{1= =}4751

w₂= =32695

f_{2= =}5206

П=f2-f1=0,4

Z_{(fp)= =}13907

Таблица №2:

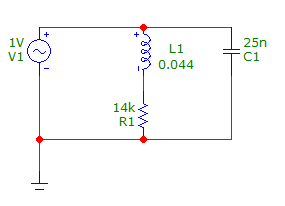
По предварительному расчету С=25 нФ L=0,041 Гн				Получено экспериментально
Q	R, Ом	fp1, кГц	Z(fp), кОм	fp1, кГц	Z(fp), кОм
2	640	4,3	2,6	4,4	2,896
100	12,8	4,9	128	5	130

R =640

W_{p= =}27057

f_p1= =4,3

W_{p= =}31233

f_p2= =4,9

Z(f_p1)=RQ²=2,6

Эксперимент:

Схема №1:

Графики:

1. Построение зависимости модуля входного сопротивления от частоты

2. Построение зависимости фазы входного сопротивления от частоты

3. Построение зависимости модуля входного тока от частоты

Схема №2:

Графики:

1. Построим график зависимости модуля входного сопротивления от частоты при Q=2

2. Построим график зависимости модуля входного сопротивления от частоты при Q=100

3. Построим график зависимости фазы входного сопротивления от частоты при Q=2

4. Построим график зависимости фазы входного сопротивления от частоты при Q=100

5. Построим график зависимости модуля входного тока(I), модуля тока в катушке(I_L), модуля тока в конденсаторе(I_C) от частоты при (U₁=1 В) для Q=2

6. Построим график зависимости модуля входного тока(I), модуля тока в катушке(I_L), модуля тока в конденсаторе(I_C) от частоты при (U₁=1 В) для Q=100

Общий вывод:

Данные и графики, полученные в результате машинного эксперимента в программе MicroCap, незначительно отличаются от предварительного расчета из-за погрешности вычислений

Вопросы для самопроверки и ответы на них:

1. Почему резонанс в параллельном пассивном колебательном контуре называется резонансом токов?

2. Как рассчитывается резонансная частота сложного параллельного колебательного контура?

3. Что такое добротность параллельного пассивного колебательного контура?

4. Что такое полоса пропускания параллельного пассивного колебательного контура? Какие существуют способы расчета полосы пропускания?

5. Выведите уравнения, с помощью которых рассчитывают входные АЧХ и ФЧХ параллельного пассивного колебательного контура.

ОТВЕТЫ НА ВОПРОСЫ

1. Резонанс в параллельном колебательном контуре называется резонансом токов ,потому что при резонансной частоте индуктивное сопротивление равно емкостному сопротивлению, а как следствие токи в цепях с индуктивностью и емкостью равны и находятся в противофазе. Поэтому ток в цепи имеет только активную составляющую.

2.  f_p=1/(2π )

3. Добротность – характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.

4. Полоса пропускания параллельного пассивного колебательного контура это диапазон частот, который определяют по резонансной кривой на уровне 0,7 от максимального значения напряжения,соответстующей резонансной частоте.

Способы расчета:

1. Графический способ (Это способ, при котором полосу пропускания определяют непосредственно по графику.)

2. Аналитический способ (Способ, при котором рассчитывают нижнюю и верхнюю граничные частоты,а потом из верхней вычитают нижнюю.)

5. Z_KK(jω)=  =  =

Так как вблизи от резонанса   L ,  , получим окончательное выражение сопротивления параллельного колебательного контура

 =  =

АЧХ: Z_ВХ(ω)=

ФЧХ: ϕ_Z(ω)=arg(z)