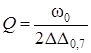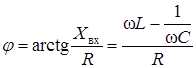лабы / лаба№4потоэ

Ордена Трудового Красного Знамени Федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики» (МТУСИ)

Предмет:

Теоретические Основы Электротехники.

Лабораторная работа №16 по теме:

“Исследование на ЭВМ резонансных явлений в пассивном и активном последовательном колебательном контуре ”

Проверил:

Волков А. С.

Москва 2023

ЦЕЛЬ РАБОТЫ:

С помощью программы Micro-Cap исследовать характеристики одиночного последовательного пассивного и активного колебательного контура при различных добротностях.

Формулы:

ZBX= -комплексное входное сопротивление контура

W0L= -резонансная частота контура

f0=

p= -характеристическое сопротивление

Q= – добротность

f1= – нижняя граничная частота

f2= – верхняя граничная частота

П=f2-f1 – абсолютная полоса пропускания

I0= – модуль входного тока при резонансе

I(w)= – резонансная кривая при условии, что меняется только частота источника напряжения

Q= - добротность последовательного контура

I1=-GU2

I2=-GU1

Z1= – входное сопротивление нагруженного гиратора

Z2=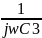 – выходное сопротивление

Z1 = jwL

L= – эквивалентная инжуктивность

f0= – резонансная частота

Таблица:

По предварительному расчёту U1=1B f0=4,8кГц C=25нФ L=0,044Гн										Получено экспериментально
R ом	p ом	Q	f1 кГЦ	f2 кГЦ	П кГЦ	I0 мА	f0 кГЦ	f0 кГЦ			I0 А	f1 кГЦ	f2 кГЦ	П кГЦ	Q
160	1326	8,28	4,8	4,817	0,017	6,25	4,8	4,796			6,25	4,8	4,9	0,23	8,3
640	1326	2,07	4,8	5,072	0,272	1,563	4,8	4,796			1,56	4,4	5,2	0,9	2,0
Гиратор
По предварительному расчёту U1=1B, f0=5кГц, C2=1мкФ, G=0,1См										Получено экспериментально
R, Ом				C1, мкФ					f0, кГц
0,1				10,14					5

С=25*10^-9 Ф

2пf0= , L= =0,044 Гн

p= =1326 Ом

Q= =8,28

f1= =4800

f2= =4817

П=f2-f1=17

I0= = 0,00625=6,3 мА

C1=

Эксперимент:

Схема №1:

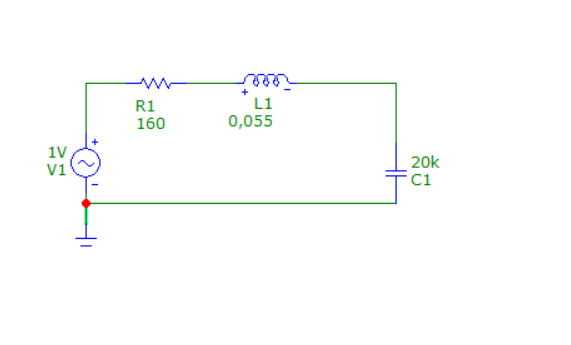
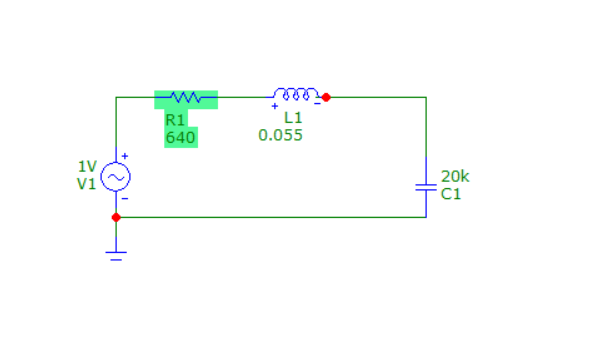
Схема №2:

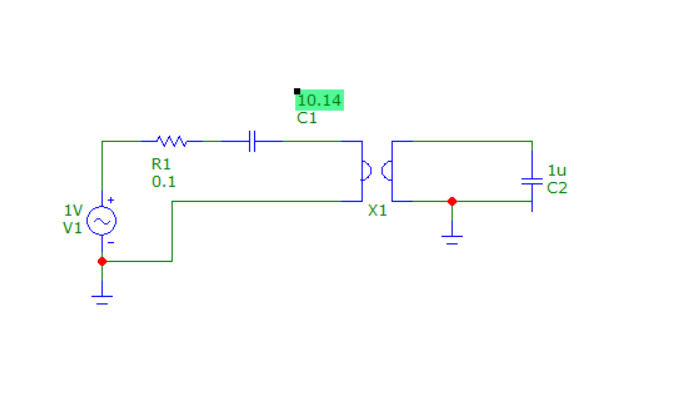
Графики:

1. Построение зависимости модуля входного сопротивления от частоты

Для 160:

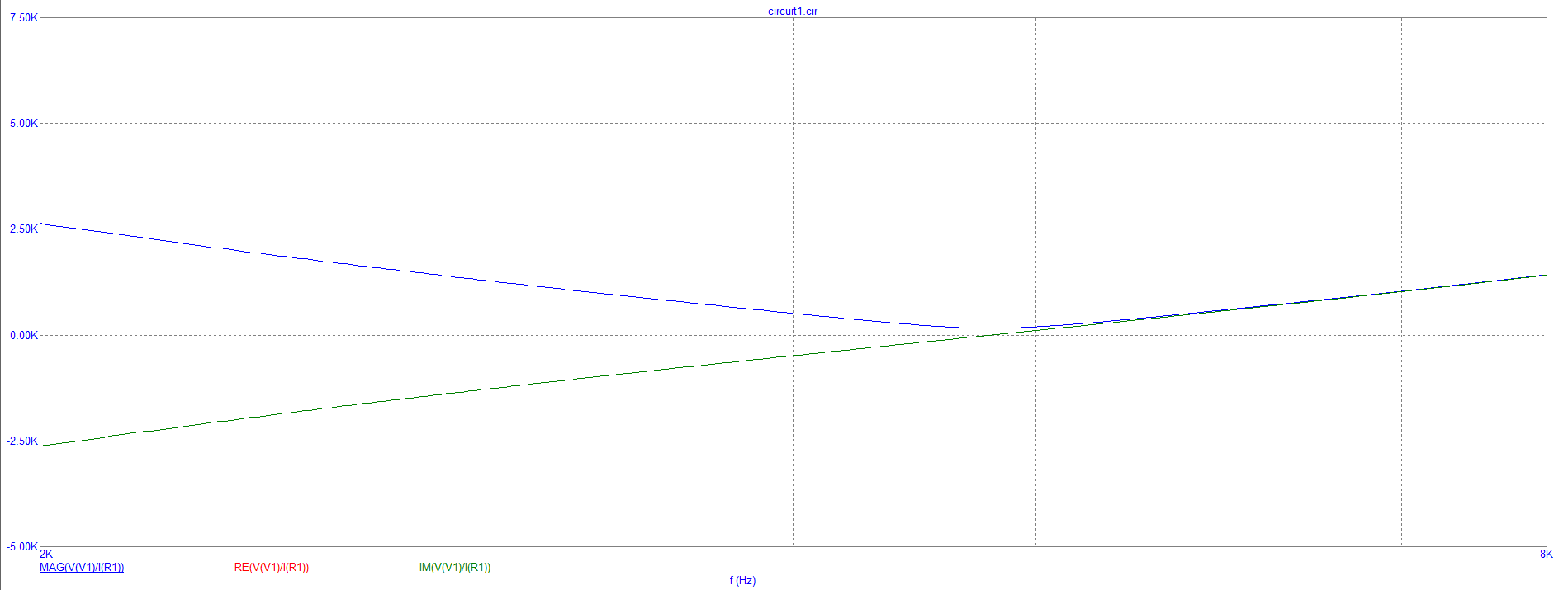
Для 640:

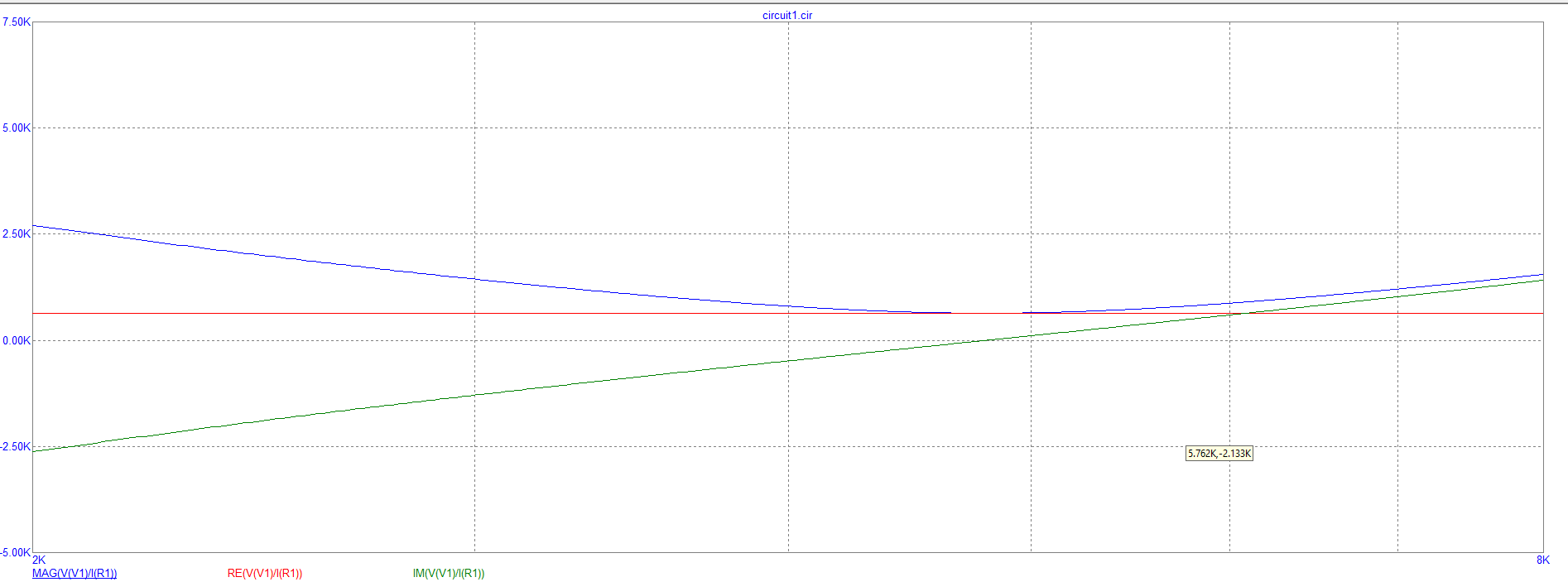
2. Построение зависимости фазы входного сопротивления от частоты

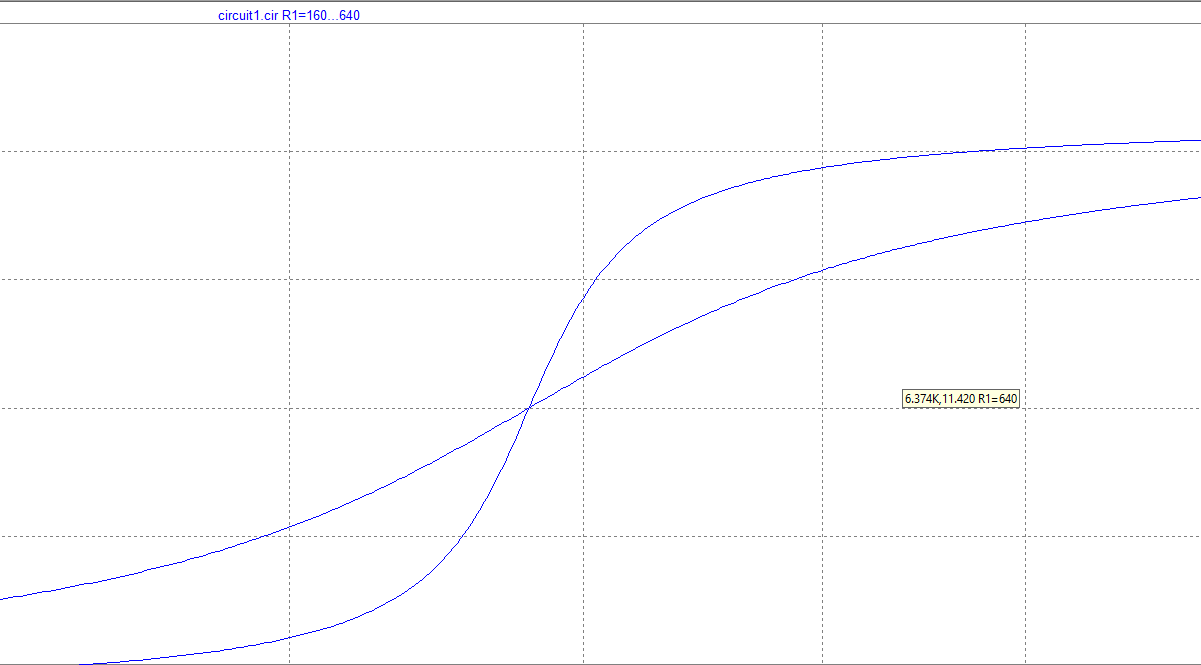
3. Построение зависимости модуля входного тока от частоты

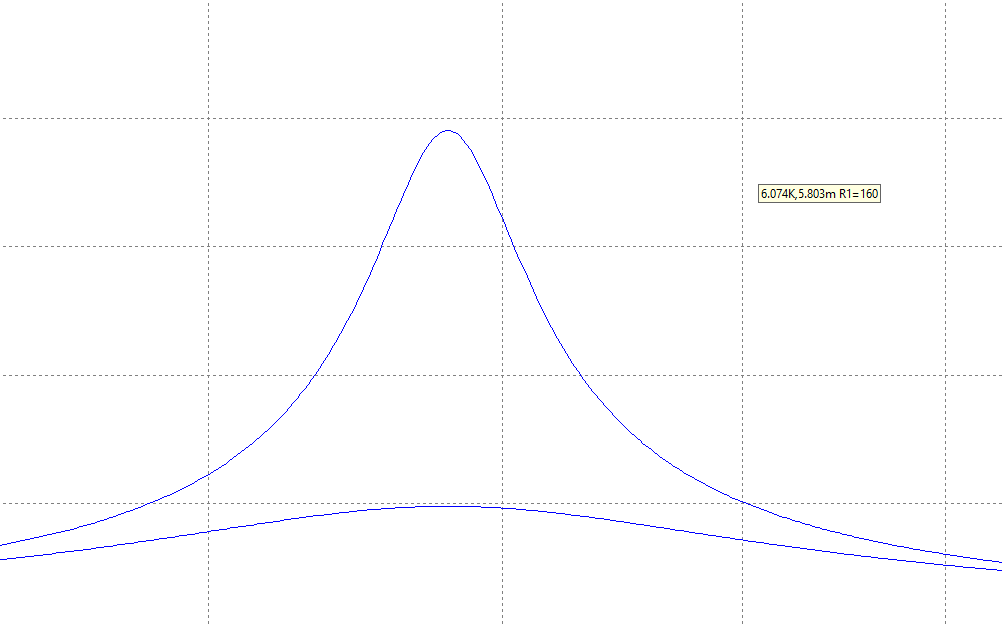
4. Построение зависимости модуля входного тока от частоты при изменении параметров индуктивности (L₁ = 0.044 Гн и L₂ = 0,088 Гн).

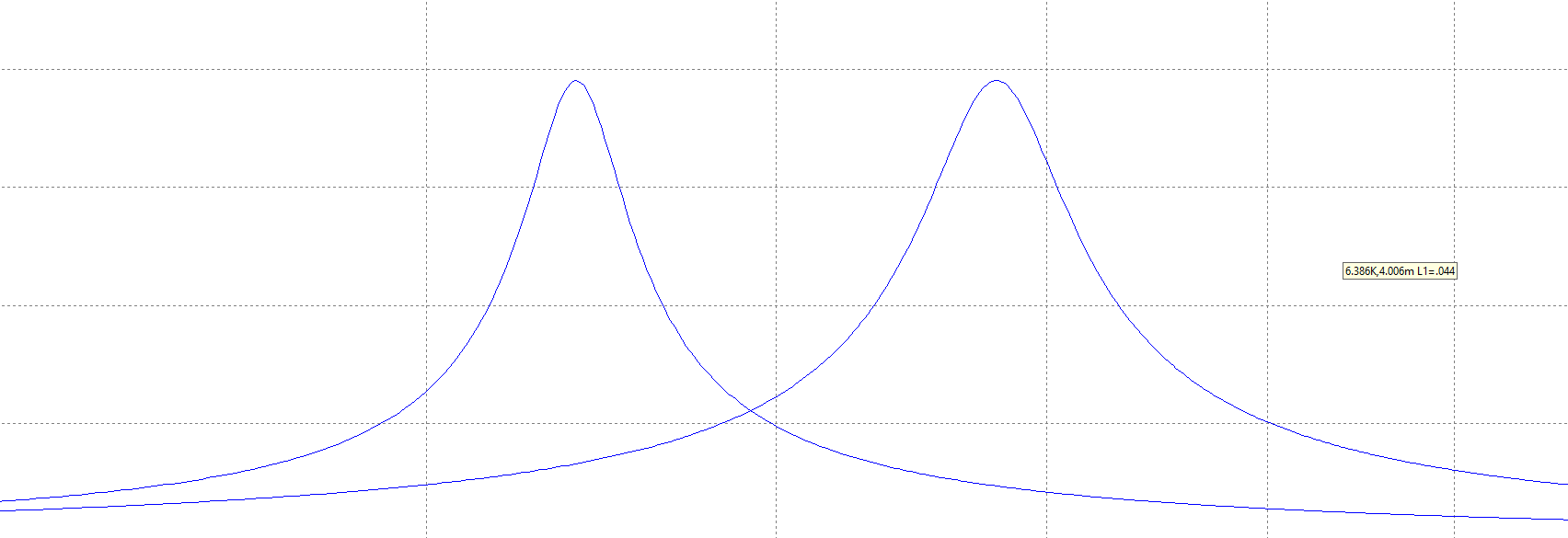
5. Построение зависимости модуля входного тока от частоты при изменении параметров емкости (C₁ = 25нФ и C₂ = 50нФ).

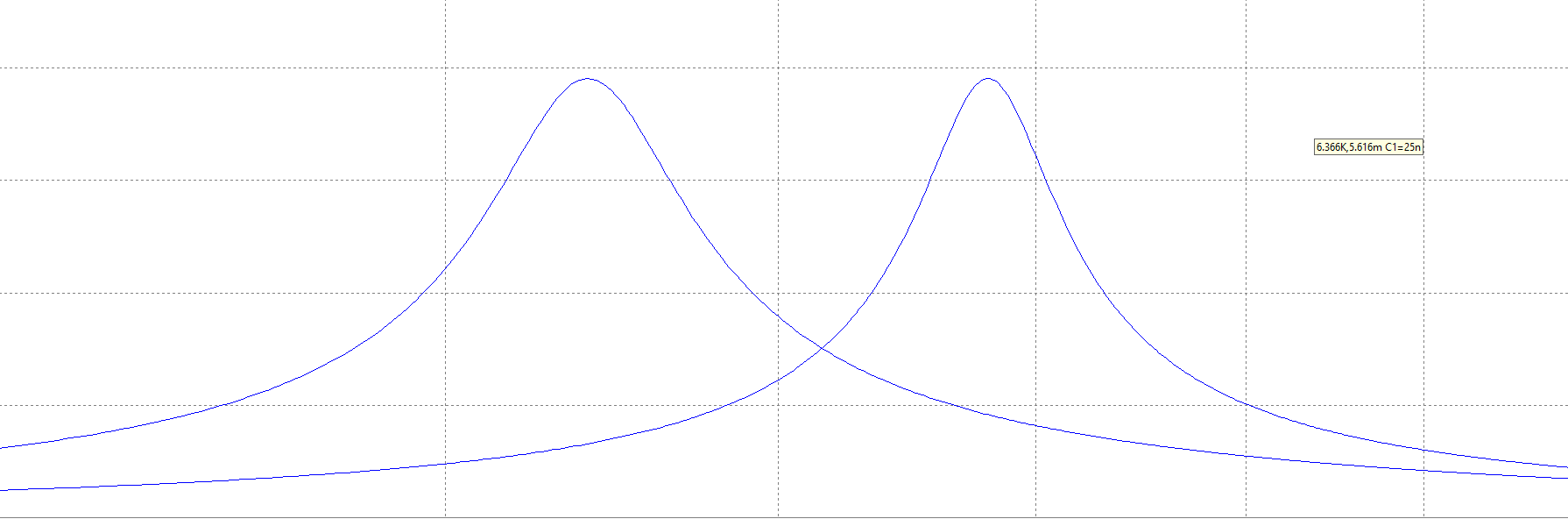
6. Построение зависимости модуля тока от частоты в схеме с гиратором

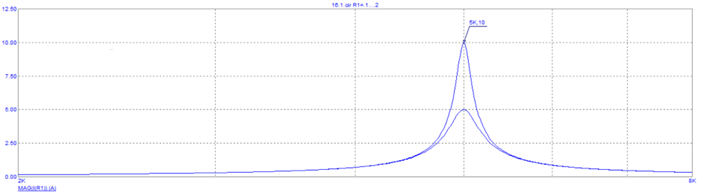
Общий вывод:

Данные и графики, полученные в результате машинного эксперимента в программе MicroCap, незначительно отличаются от предварительного расчета из-за погрешности вычислений

Вопросы для самопроверки и ответы на них

1. Почему резонанс в последовательном пассивном колебательном контуре называется резонансом напряжений?

2. Как рассчитывается резонансная частота сложного пассивного колебательного контура и как она рассчитывается для схем содержащих гиратор?

3. Что такое добротность последовательного пассивного колебательного контура?

4. Что такое полоса пропускания последовательного пассивного колебательного контура? Какие существуют способы расчета полосы пропускания?

5. Выведите уравнения, с помощью которых рассчитывают входные АЧХ и ФЧХ последовательного пассивного колебательного контура.

ОТВЕТЫ НА ВОПРОСЫ

1)На любой частоте, кроме резонансной, напряжения на индуктивности и емкости отличаются - они зависят от амплитуды тока в схеме и номиналами модулей реактивных сопротивлений X_L и X_С. Поэтому резонанс в последовательном колебательном контуре называют резонансом напряжений.

– резонансная частота контура.

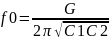– резонансная частота активного последовательного колебательного контура с гиратором в качестве индуктивности.

3)Добротность последовательного колебательного контура – величина, определяющая амплитуду и ширину АЧХ (амплитудно-частотные характеристики) резонанса и говорящая о том, во сколько раз сохраненной энергии в колебательном контуре больше, чем потери энергии за единичный период колебаний.

4) Полоса пропускания — диапазон частот, в пределах которого амплитудно-частотная характеристика акустического, радиотехнического, оптического или механического устройства достаточно равномерна для того, чтобы обеспечить передачу сигнала без существенного искажения его формы.

Рассчитать полосу пропускания можно с помощью следующих расчетных формул: Абсолютная полоса пропускания:

5) Зависимость тока в контуре или напряжения на реактивных элементах от частоты питающего генератора при постоянном по величине напряжении генератора называется резонансной кривой или амплитудно-частотной характеристикой контура.

 

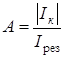
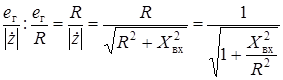
Реактивная составляющая входного сопротивления контура равна: 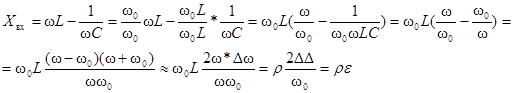  Здесь   - относительная расстройка контура. Для небольших абсолютных расстроек контура    (в пределах полосы пропускания)    С учетом этого амплитудно-частотная характеристика контура 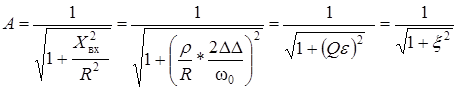Где:    - обобщенная расстройка контура. Окончательно уравнение амплитудно-частотной характеристики контура запишется в виде: 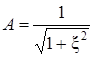  Фазовая характеристика контура    При настройке контура в резонанс   , обобщенная расстройка   , реактивная составляющая входного сопротивления равна нулю и эквивалентное сопротивление контура равно   . Характер зависимости   свидетельствует о том, что колебательный контур обладает свойством избирательности. Количественно избирательность контура оценивается коэффициентом прямоугольности   , который равен отношению ширины резонансной кривой на уровне 0,7 к ширине на уровне 0,1. Чем больше значение добротности, тем лучше избирательность контура. Для одиночных колебательных контуров      АЧХ последовательного контура Найдем выражение для полосы пропускания колебательного контура. Полоса пропускания оценивается по уменьшению тока в контуре или напряжений на реактивных элементах в    раз по сравнению с их значениями на резонансной частоте. 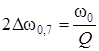Из формулы для АЧХ контура найдем полосу пропускания:   Отсюда полоса пропускания контура на уровне    Будет равна:    Зная резонансную частоту и полосу пропускания, можно рассчитать добротность контура: