лабы / лаба№2потоэ
.docxОрдена Трудового Красного Знамени Федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики» (МТУСИ)
Предмет:
Теоретические Основы Электротехники.
Лабораторная работа №32 по теме:
“Исследование пассивных цепей при гармоническом воздействии на постоянной частоте”
Проверил:
Волков А. С.
Москва 2023
ЦЕЛЬ РАБОТЫ
С помощью программы Micro-Cap исследовать электрический режим конденсатора и катушки индуктивности в цепях гармонического тока. Сравнить полученные характеристики с помощью программы Micro-Cap, с аналогичными характеристиками, полученными расчетным путем.
Формулы:
Комплексное сопротивление двухполюсника можно рассчитать следующим образом:
,
Где
R=Re(Z) – резистивное сопротивление двухполюсника;
X=Im(Z) – реактивное сопротивление двухполюсника;
|Z|=Z – модуль комплексного сопротивления двухполюсника;
Ф=arg(Z) – аргумент (фаза) комплексного сопротивления двухполюсника;
f – частота;
j=
– мнимая единица
Для С-цепи
Zc=-jXc=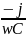
=
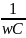e^-j*90
=
=|
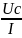|*e^j*arg(
)
– комплексное сопротивление конденсатора;
Xc= – ёмкостное сопротивление конденсатора.
Для L-цепи
Zl=jxl=jwL=wL*e^j90
=
=|
|e^j*arg(
)
– комплексное сопротивление катушки;
Xl=wL – индуктивное сопротивление катушки.
Закон Ома для комплексных величин
I=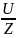
– комплексный ток;
U=Z*I – комплексное падение напряжения;
Ul=jwL*I=|Ul|e^j90 - комплексное напряжение на катушке;
Uc= *I=|Uc|e^-e90 - комплексное напряжение на конденсаторе.
Предварительный расчёт:
3.1
Рассчитать в алгебраической форме комплексное сопротивление конденсатора Zc, определить его полное сопротивление |Zc| (модуль) и аргумент arg|Zc| (фазу) на пяти частотах 1, 2, 3, 4 и 5 кГц, если С=38,7 нФ.
По предварительному расчету |
Получено экспериментально |
||||||
f, кГц |
C, нФ |
Zc, Ом |
|Zc|, Ом |
Arg(Zc), град. |
|Zc|, Ом |
Arg(Zc), град. |
|
1 |
38,7 |
-j*4115 |
4115 |
-90 |
4113 |
-90 |
|
2 |
38,7 |
-j*2057 |
2057 |
-90 |
2056 |
-90 |
|
3 |
38,7 |
-j*1372 |
1372 |
-90 |
1371 |
-90 |
|
4 |
38,7 |
-j*1029 |
1029 |
-90 |
1028 |
-90 |
|
5 |
38,7 |
-j*823 |
823 |
-90 |
823 |
-90 |
|
Найдём
Zc
по формуле
=
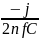
Найдём
|Zc|
по формуле
3.2
Рассчитать в алгебраической форме комплексное сопротивление ZRC RC-цепи для пяти частот 1, 2, 3, 4 и 5 кГц, определить его полное сопротивление и аргумент, если R=3 кОм, С=38,7 нФ.
По предварительному расчёту |
Получено экспериментально |
|||||||
f, кГц |
C, нФ |
R, кОм |
ZRC, Ом |
|ZRC| Ом |
Arg|ZRC|, град |
|ZRC| Ом |
Arg|ZRC|, град |
|
1 |
38,7 |
3 |
3*10^3-j*4115 |
5090 |
-53 |
5090 |
-53 |
|
2 |
38,7 |
3 |
3*10^3-j*2057 |
3637 |
-34 |
3637 |
-34 |
|
3 |
38,7 |
3 |
3*10^3-j*1372 |
3298 |
-24 |
3298 |
-24 |
|
4 |
38,7 |
3 |
3*10^3-j*1029 |
3171 |
-18 |
3171 |
-18 |
|
5 |
38,7 |
3 |
3*10^3-j*823 |
3110 |
-15 |
3111 |
-15 |
|
Найдём ZRC по формуле ZR+Zc=R -
Найдём
|ZRC|
по формуле
Найдём
Arg|ZRC|
по формуле arctg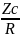
3.3
Рассчитать напряжения на конденсаторе U2=U2e^jф , если U1=0,707e^j0 на частотах 1, 2, 3, 4 и 5 кГц, определить его модуль и фазу.
По предварительному расчёту |
Получено экспериментально |
|||||||
f, кГц |
C, нФ |
R, кОм |
U1, B |
U2, B |
Ф, град |
U2, B |
U2, B |
Ф, град |
1 |
38,7 |
3 |
0,707 |
0.807 |
-36.11 |
0.807*e^-j36,11 |
807 |
-36.11 |
2 |
38,7 |
3 |
0,707 |
0.565 |
-55.572 |
0.565* e^-j56 |
565 |
-55.572 |
3 |
38,7 |
3 |
0,707 |
0.415 |
-65.442 |
0.415* e^-j65 |
415 |
-65.442 |
4 |
38,7 |
3 |
0,707 |
0.324 |
-71.083 |
0.324* e^-j71 |
324 |
-71.083 |
5 |
38,7 |
3 |
0,707 |
0.264 |
-74.668 |
0.264* e^-j75 |
264 |
-74.668 |
3.4
Рассчитать в экспоненциальной форме комплексное сопротивление катушки индуктивности ZL для пяти частот 1, 2, 3, 4 и 5 кГц, определить её полное сопротивление и аргумент, если L=31 мГн.
По предварительному расчёту |
Получено экспериментально |
||||||
f, кГц |
L, мГн |
ZL, Ом |
|ZL|, Ом |
Arg(ZL), град |
|ZL|, Ом |
Arg(ZL), град |
|
1 |
31 |
j*194.8 |
194.8 |
90 |
194 |
90 |
|
2 |
31 |
j*389.6 |
389.6 |
90 |
389 |
90 |
|
3 |
31 |
j*584 |
584 |
90 |
584 |
90 |
|
4 |
31 |
j*779 |
779 |
90 |
779 |
90 |
|
5 |
31 |
j*974 |
974 |
90 |
973 |
90 |
|
Найдём ZL по формуле: j*2*п*f*L
3.5
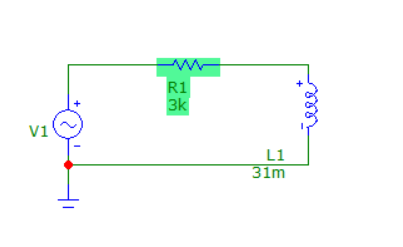
Рассчитать в алгебраической форме комплексное сопротивление ZRL RL-цепи для пяти частот 1, 2, 3, 4 и 5 кГц, определить его полное сопротивление и аргумент, если R=3 кОм, L=31 мГн.
По предварительному расчёту |
Получено экспериментально |
||||||
f, кГц |
L, мГн |
R, кОм |
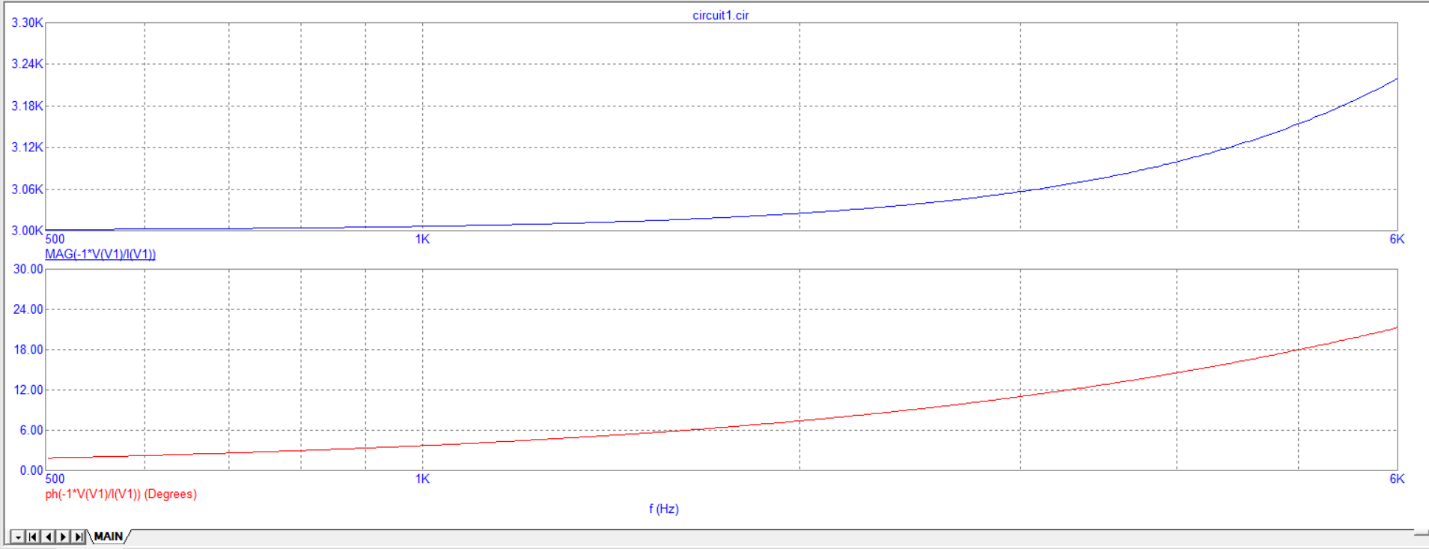
ZRL, Ом |
|ZRL|, Ом |
Arg(ZRL), Град |
|ZRL|, Ом |
Arg(ZRL), Град |
1 |
31 |
3 |
3*10^3+ j*194.8 |
3006 |
3.715 |
3006 |
3.715 |
2 |
31 |
3 |
3*10^3+ j*389.6 |
3025 |
7.399 |
3025 |
7.399 |
3 |
31 |
3 |
3*10^3+ j*584 |
3056 |
11.022 |
3056 |
11.022 |
4 |
31 |
3 |
3*10^3+ j*779 |
3099 |
14.558 |
3100 |
14.558 |
5 |
31 |
3 |
3*10^3+ j*974 |
3154 |
17.985 |
3154 |
17.985 |
Найдём ZRL по формуле: R+j*2*п*f*L
3.6
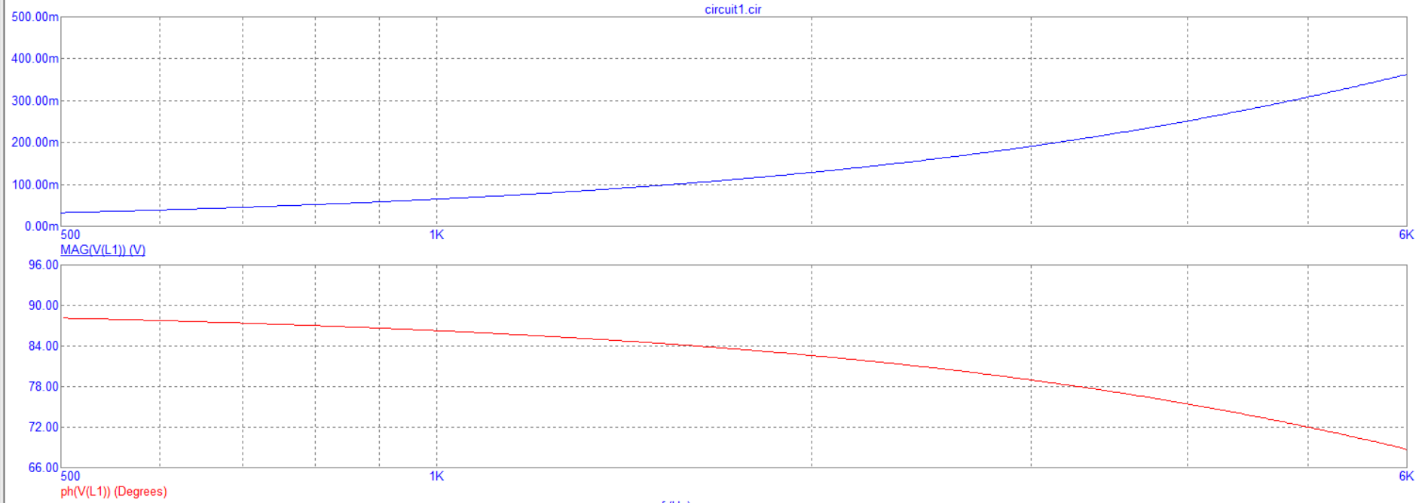
Рассчитать напряжения на катушке индуктивности U2=U2e^jф , если U1=0,707e^j0 для пяти частот 1, 2, 3, 4 и 5 кГц, определить его модуль и фазу.
По предварительному расчёту |
Получено экспериментально |
|||||||
f, кГц |
L, мГн |
R, кОм |
U1, B |
U2, B |
Ф, град |
U2, B |
U2, B |
Ф, град |
1 |
31 |
3 |
0,707 |
0.065 |
86.285 |
0.065*e^86.285 |
0.065 |
86.285 |
2 |
31 |
3 |
0,707 |
0.129 |
82.601 |
0.129*e^82.601 |
0.129 |
82.601 |
3 |
31 |
3 |
0,707 |
0.191 |
78.978 |
0.191*e^78.978 |
0.191 |
78.978 |
4 |
31 |
3 |
0,707 |
0.251 |
75.442 |
0.251*e^75.442 |
0.251 |
75.442 |
5 |
31 |
3 |
0,707 |
0.309 |
72.015 |
0.309*e^72.015 |
0.309 |
72.015 |
Эксперименты:
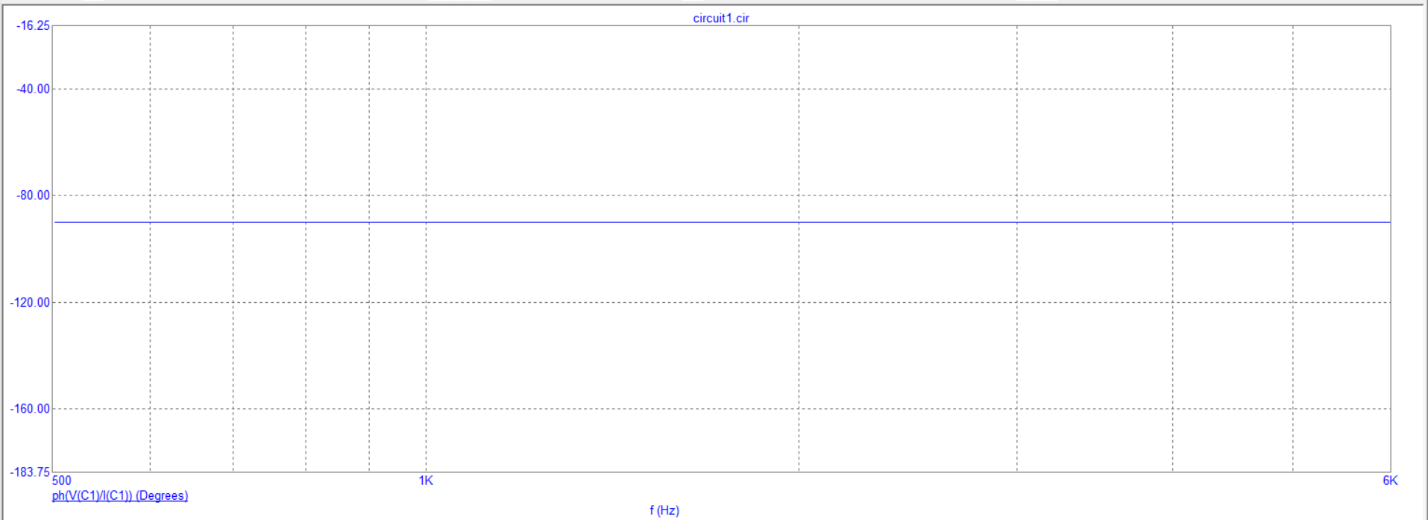
Эксперимент №1 1) Сборка С-цепи
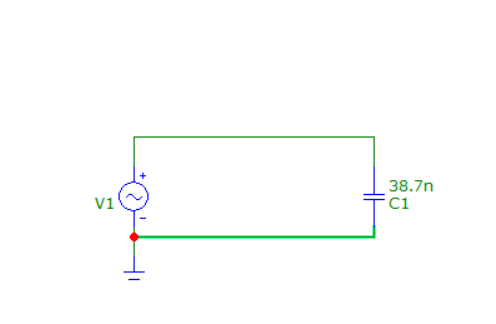
2) Исследование модуля и фазы комплексного сопротивления C-цепи.
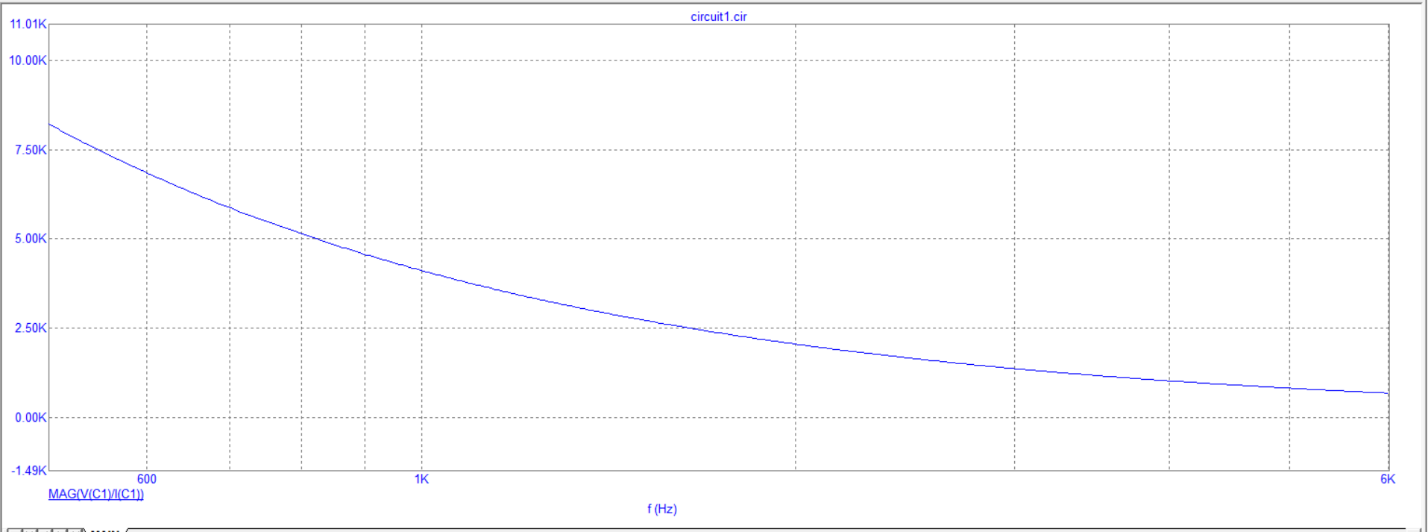
3) Построение зависимости фазы сопротивления С-цепи от частоты.
Эксперимент №2 1) Сборка RC-цепи.
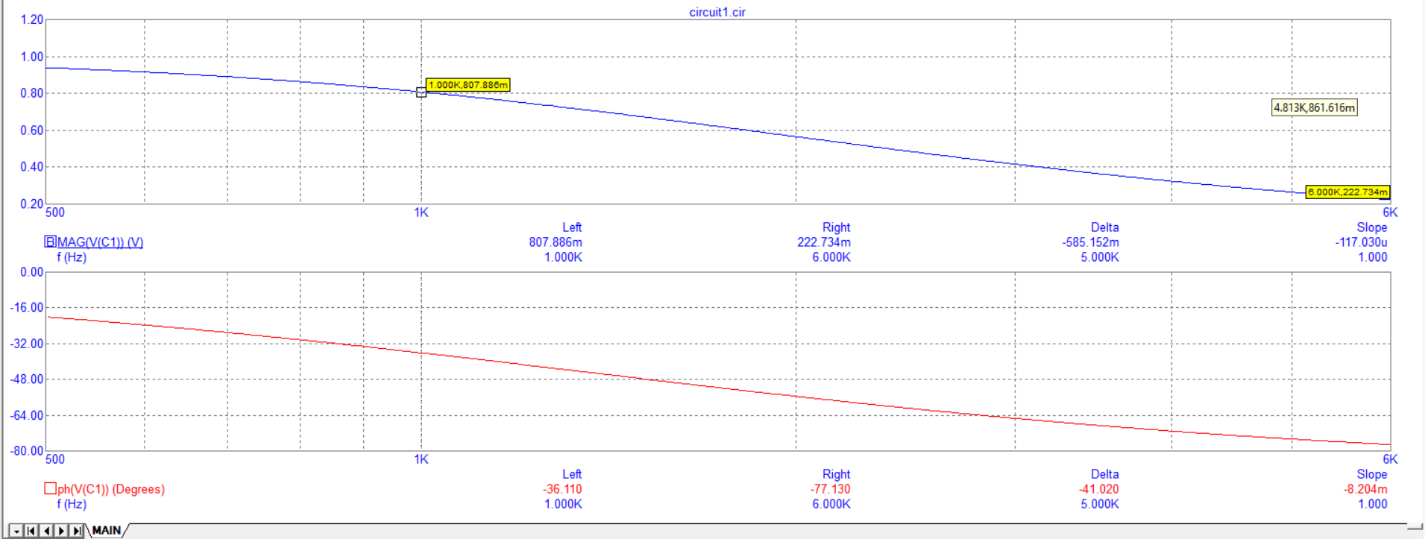
2) Исследование модуля и фазы комплексного сопротивления RC-цепи.
3) Исследование модуля и фазы комплексного напряжения на конденсаторе RC-цепи.
Эксперимент №3
1)Сборка L-цепи.
2) Исследование модуля и фазы комплексного сопротивления L-цепи.
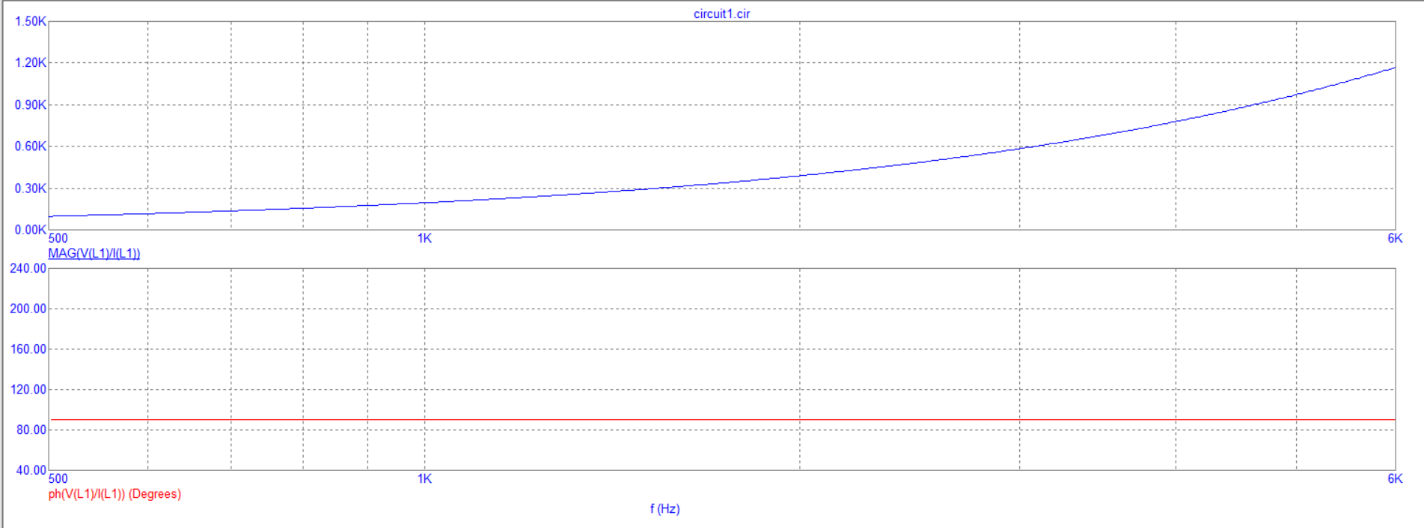
Эксперимент №4
1) Сборка RL-цепи.
2) Исследование модуля и фазы комплексного сопротивления RL-цепи.
3) Исследование модуля и фазы комплексного напряжения на катушке RL-цепи.
Общий вывод:
Данные и графики, полученные в результате машинного эксперимента в программе MicroCap, незначительно отличаются от предварительного расчета из-за погрешности вычислений
Вопросы для самопроверки и ответы на них
Какая частота называется граничной для RL-цепи?
Граничная частота - это частота, при которой модуль реактивного сопротивления равен активному сопротивлению. Для RL-цепи это означает: ωL = R или 2πfL = R
Каково значение модуля входного сопротивления RL-цепи на граничной частоте?
Входное сопротивление ZRL = ZR + ZL = R + jwL
|ZRL|
=
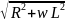
Так
как на граничной частоте wL
= R, то |ZRL|
= 
= R*
Каково значение аргумента входного сопротивления RL-цепи на граничной частоте?
Arg(ZRL)=arctg(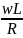
)
Так
как на граничной частоте wL
= R, то arg(ZRL)=
arctg(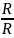
)=
45 град.
К чему стремится модуль тока RL-цепи при увеличении частоты?
Так
как I=
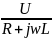, то при w->
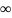I
-> 0
Чему равен модуль входного сопротивления RL-цепи при частоте равной нулю?
Входное сопротивление ZRL=ZR + ZL = R + jwL При w=0 ZRL=R