лабы / лаба

Ордена Трудового Красного Знамени Федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики» (МТУСИ)

Предмет:

Теоретические Основы Электротехники.

Лабораторная работа №31 по теме:

“Исследование входных частотных характеристик в RL-цепи”

Проверил:

Волков А. С.

Москва 2023

Цель работы:

С помощью программы Micro-Cap исследовать входные амплитудно-частотные(АЧХ) и фазочастотные(ФЧХ) характеристики RL-цепи. Сравнить АЧХ и ФЧХ, полученные с помощью программы Micro-Cap, с аналогичными характеристиками, полученными расчётным путём.

Данные:

R1=100 Ом

L1=45 мГн

E=0,9 B

Формулы:

ZBX=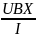 =Z(w)e^jфz(w)=Z(2пf)e^fфz(2пf)

Где

UBX – комплексное входное напряжение;

I=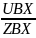 – комплексный входной ток;

UR=R*I – комплексное напряжение на резисторе;

J=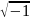 – мнимая единица;

w=2пf – угловая скорость;

f – частота;

UL=jwL*I – комплексное напряжение на катушке;

|ZBX|=Z(2пf) – модуль комплексного входного сопротивления (АЧХ);

Arg(ZBX)=фz(2пf) – аргумент (фаза) комплексного входного сопротивления (ФЧХ);

С другой стороны, входное сопротивление это сопротивление со стороны входных зажимов

ZBX = Re(ZBX) + jIm(ZBX)=R1 + jXL= 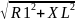* e^-j*arctg( 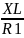) = R1*

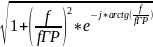
Re(ZBX)=R1 – резистивное входное сопротивление (равно сопротивлению резистора R1),

Im(ZBX)=XL – реактивное входное сопротивление,

fГР=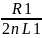 – граничное частота RL-цепи.

Таблица:

По предварительному расчёту:

f, кГц	f/fГр	XL, Ом	ZBX, Ом	Фz(f), град	I, мА	UR, B	UL, B
2	5,65	565,2	567	80	1,74	174	983,5
4	11,3	1130,4	1132	85	0,88	88	995
6	17	1695,6	1697	86,6	0,588	58,8	997
8	22,6	2260,8	2262	87,4	0,441	44,1	997
10	28,2	2826	2827	88	0,337	33,7	998
12	33,9	3391,2	3392	88,3	0,175	17,5	999
14	39,5	3956,4	3957	88,6	0,174	17,4	999

fГр=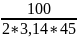 =0,354

f/fГр=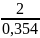 =5,65

XL=wL=2пfL=2*3,14*2*45=565,2

ZBX=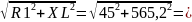 567

Фz(f)= arctg(5,65) = 80

I= =

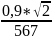
UR=R*I=100*1,74=174

UL=jwL*I=2пfL*I=983,5

Получено экспериментально:

f, кГц	XL, Ом	ZBX, Ом	Фz(f), град	I, мА	UR, B	UL, B
2	574,3	565,5	79	1,74	174,2	984,7
4	1135	1131	84	0,88	88	996,1
6	1699	1697	86	0,588	58,9	998,3
8	2264	2262	87,3	0,441	44,2	999
10	2829	2828	88	0,337	35,3	999,4
12	3395	3393	88,3	0,175	29,5	999,6
14	3960	3957	88,6	0,174	25,3	999,7

Эксперимент:

Схема:

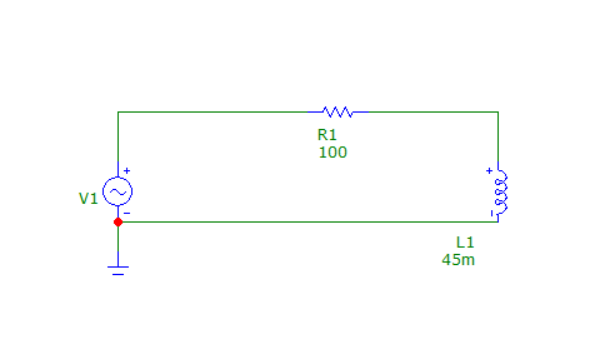
Графики:

1. Построение зависимости модуля входного сопротивления от частоты

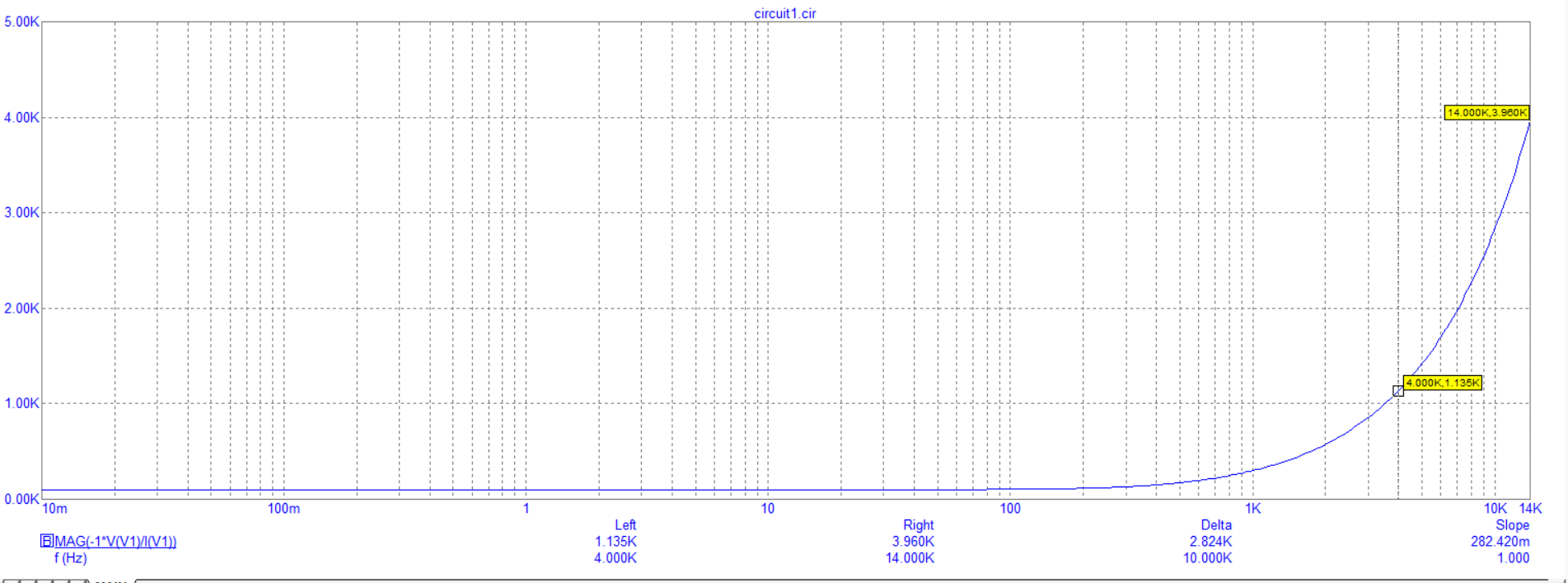
2. Построение зависимости фазы входного сопротивление от частоты

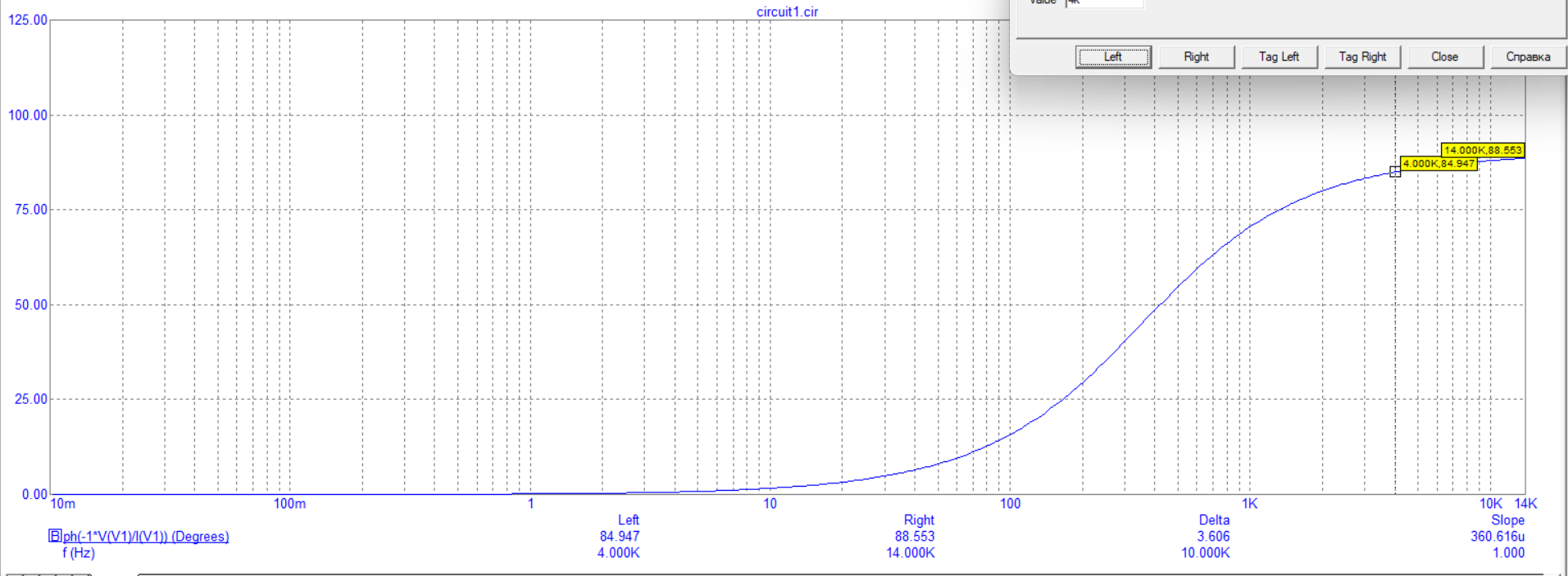
3. Построение зависимости модуля тока от частоты

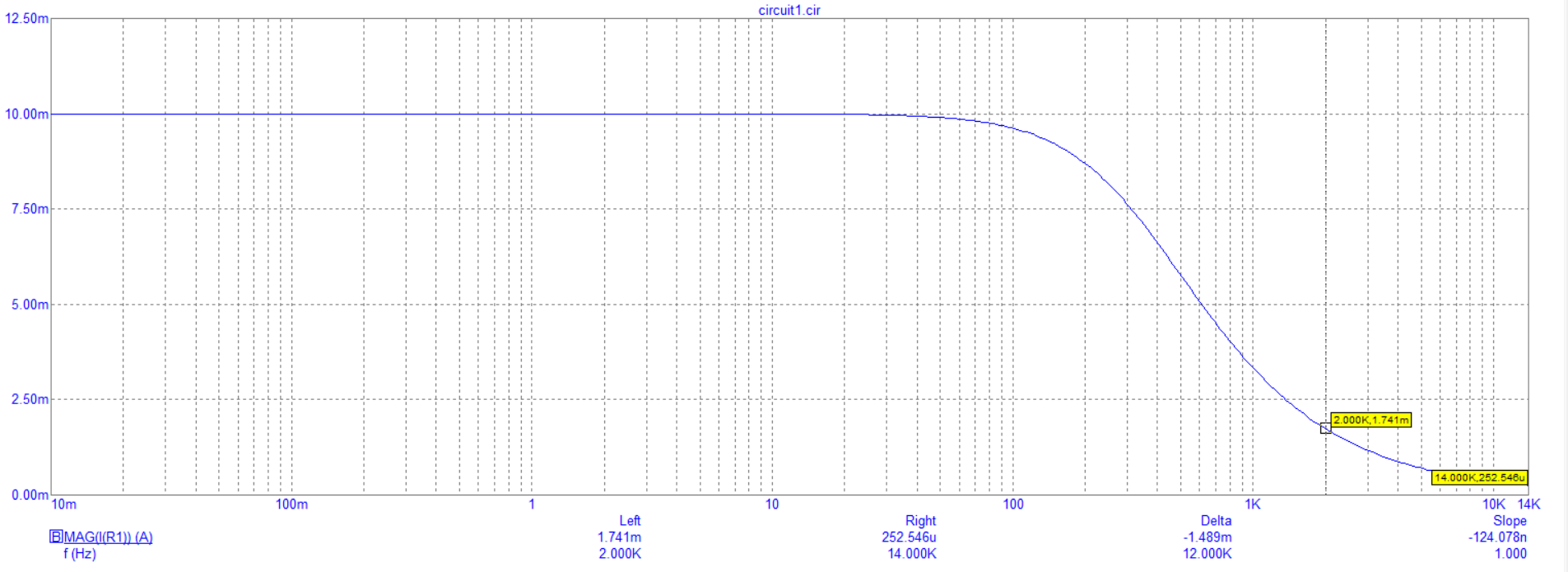
4. Построение зависимости модуля напряжения на резисторе от частоты

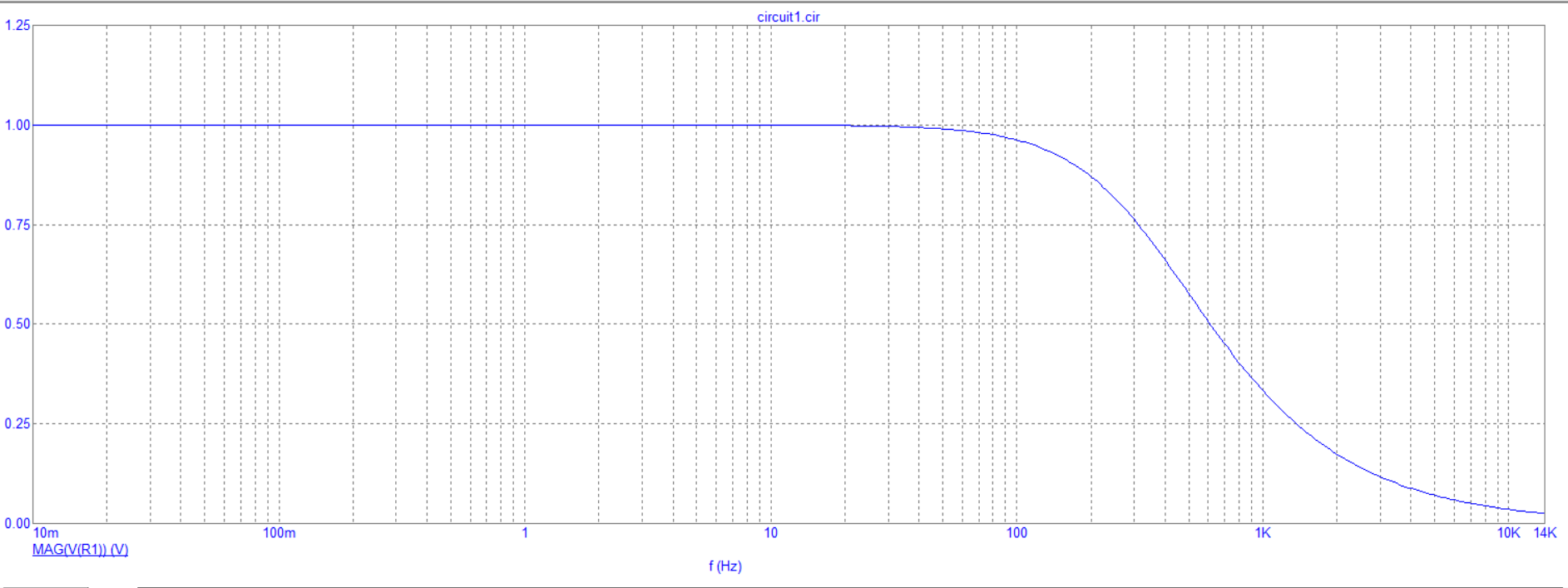
5. Построение зависимости резистивного сопротивления от частоты

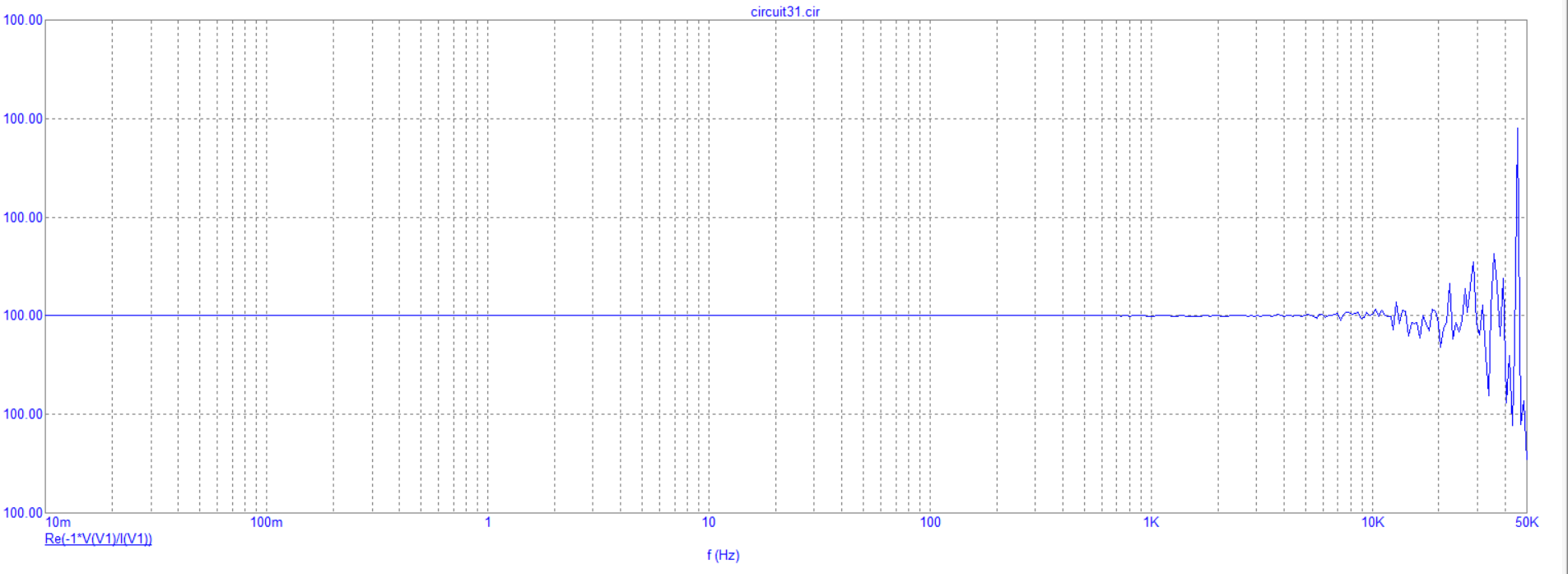
6. Построение зависимости индуктивного сопротивления от частоты

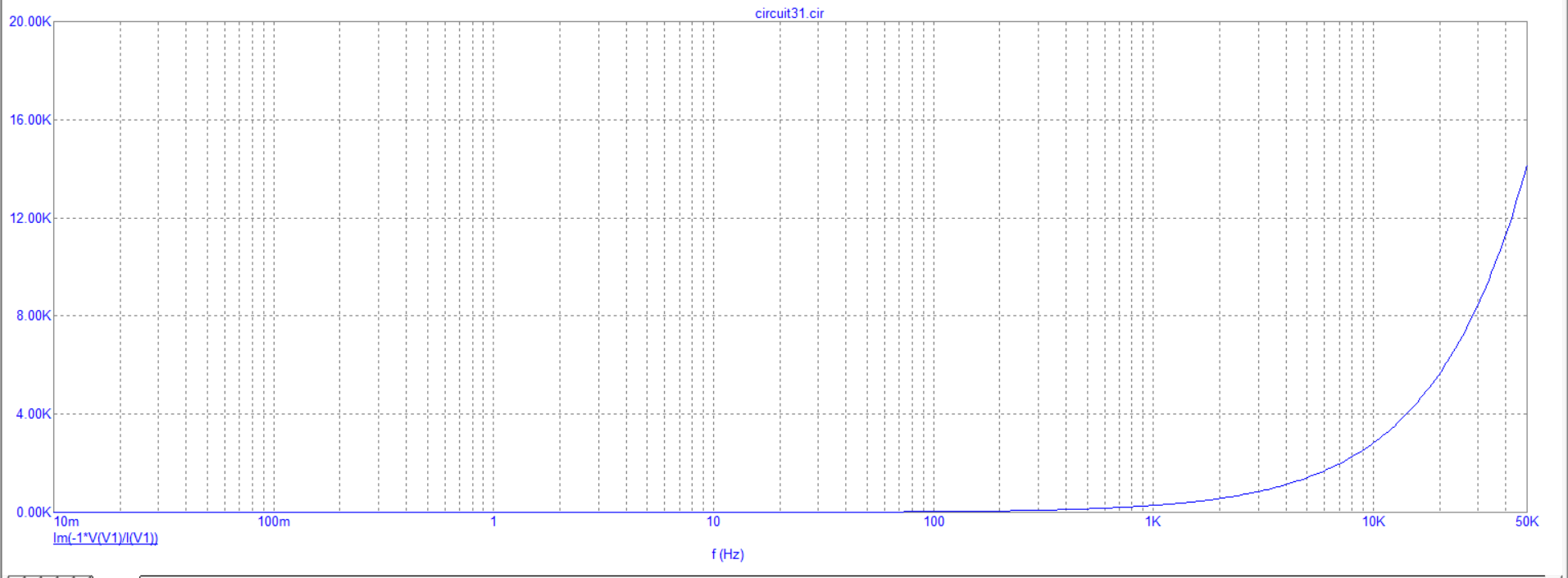
7) Построение зависимости модуля напряжения на катушке от частоты

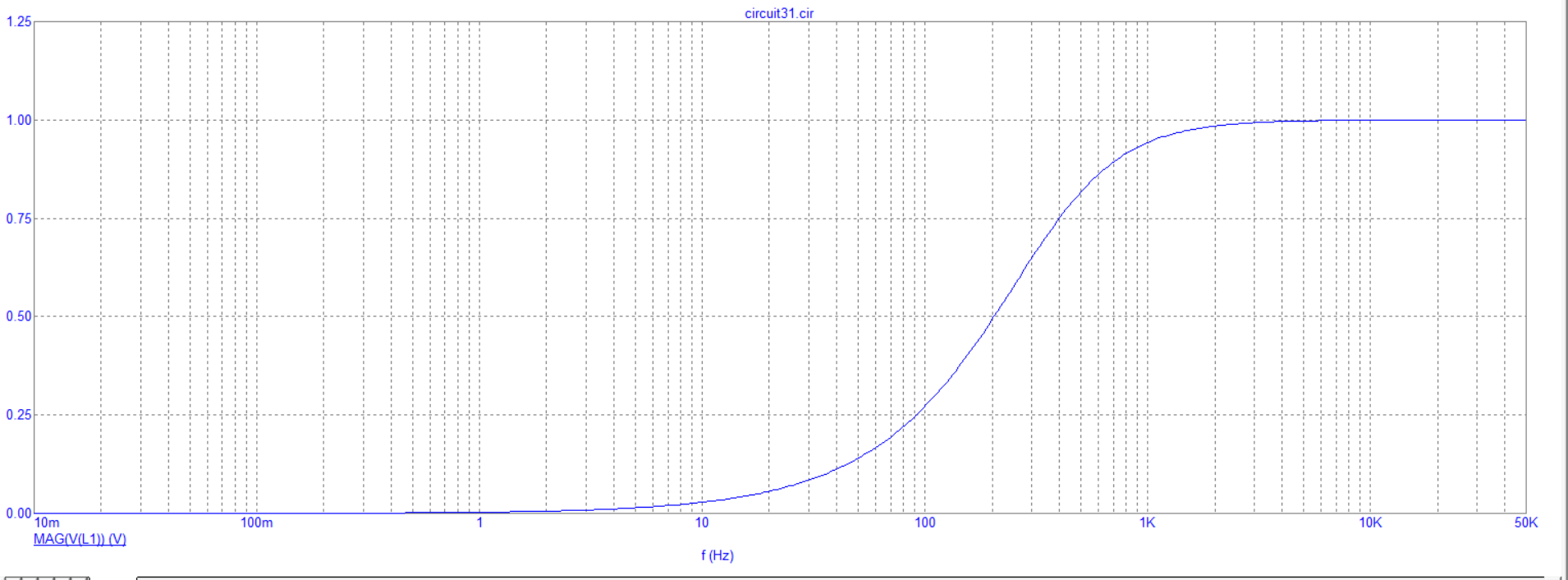
Общий вывод:

Данные и графики, полученные в результате машинного эксперимента в программе MicroCap, незначительно отличаются от предварительного расчета из-за погрешности вычислений

Вопросы для самопроверки и ответы на них

1. Какая частота называется граничной для RL – цепи?

Ответ: Частота, на которой действительная и мнимая часть комплексного входного сопротивления равны, называется граничной. R=jX

Для RL – цепи: R=wгр L

wгр=2πfгр

wгр=RL

2πfгр=RL

fгр=𝑅2π𝐿 – граничная частота для RL – цепи.

fгр=15,4 103 Гц

2. Каково значение модуля входного сопротивления RL – цепи на граничной частоте?

Ответ:

Z=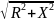

X= wгр L

wгр=2πfгр

Z=4241,28 Oм

3. Каково значение аргумента входного сопротивления RL – цепи на граничной частоте?

Ответ:

arg(Z)=𝑎𝑟𝑐𝑡𝑔(|𝑋||𝑅|)

X= wгр L

wгр=2πfгр

arg(Z)=44.98o

4. К чему стремится модуль тока RL – цепи при увеличении частоты?

Ответ:

I=ZL UZrl

I=wгр L U

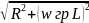
wгр=2πfгр

lim𝑓гр→∞2πfгр L U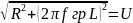

5. Чему равен модуль входного сопротивления RL – цепи при частоте равной нулю?

Ответ:

w=2πf

f=0, тогда ω=0

Z=

X= wL

Z=R

Z=3000 Oм