ПРО-332б Ихсанова ЛР 4

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное

образовательное учреждение высшего образования

«Уфимский университет науки и технологий»

Кафедра ВМиК

Отчет к лабораторной работе №4

По дисциплине «Логическое программирование»

Выполнил: 

Студентка группы ПРО-332Б:

 Ихсанова Э. А.

Проверил: 

Cтарший преподаватель кафедры ВМиК

Шакирзянов А. А.

Уфа 2024

Цель работы:

Ознакомиться с основными механизмами работы Пролога.

Задание:

Реализовать на Прологе задачи поиска совершенных чисел, генерации перестановок и сочетаний, наивной и быстрой сортировки.

Ход работы

1 задача: написать программу, которая бы находила все совершенные числа.

Код программы

%% Декларативное определение натуральных чисел

ints(0).

ints(X) :- ints(Y), X is Y + 1.

%% Сумма делителей числа

sum_divisors(Num, Sum) :- sum_divisors(Num, 1, Sum).

sum_divisors(Num, Num, Num) :- !.

sum_divisors(Num, Div, Sum) :-

Rem is Num mod Div,

(Rem = 0 ->

NextDiv is Div + 1,

sum_divisors(Num, NextDiv, TempSum),

Sum is TempSum + Div

;

NextDiv is Div + 1,

sum_divisors(Num, NextDiv, Sum)

).

%% Проверка на совершенное число

perfect_number(X) :- sum_divisors(X, Sum), X =:= Sum / 2.

%% Поиск всех совершенных чисел в заданном диапазоне

find_perfect_numbers(Start, End, PerfectNumbers) :-

findall(N, (between(Start, End, N), perfect_number(N)), PerfectNumbers),

write(PerfectNumbers), nl.

%% Пример использования:

:- find_perfect_numbers(1, 10000, _).

Результат работы

Ищем совершенные числа в диапазоне от 1 до 10000.

Р исунок 1

Рисунок 2

Этот код определяет сумму делителей числа, проверяет, является ли число совершенным, и затем находит все совершенные числа в заданном диапазоне. Переменная PerfectNumbers используется как аргумент в предикате findall, и затем мы выводим найденные совершенные числа с помощью write(PerfectNumbers).

2 задача: написать программу, которая бы генерировала перестановки.

Код программы

%% Если исходный список пустой, то существует одна перестановка - пустой список

perm([], []).

%% Генерация перестановок

perm(Source, [Element|Tail]) :-

member_list_exclude(Element, Source, SourceExcluded),

perm(SourceExcluded, Tail).

%% Проверка того, что элемент содержится в списке, а 2-й список является списком без элемента

%% Название предиката member_list_exclude соответствует порядку аргументов:

%% 1-й - элемент, 2-й - список, 3-й - список без элементов

member_list_exclude(X, [X|L], L).

member_list_exclude(X, [Y|L], [Y|Ls]) :- member_list_exclude(X, L, Ls).

%% Пример использования:

%% Генерация всех перестановок списка [1, 2, 3]

:- perm([1, 2, 3, P), write(P), nl, fail.

Результат работы

Г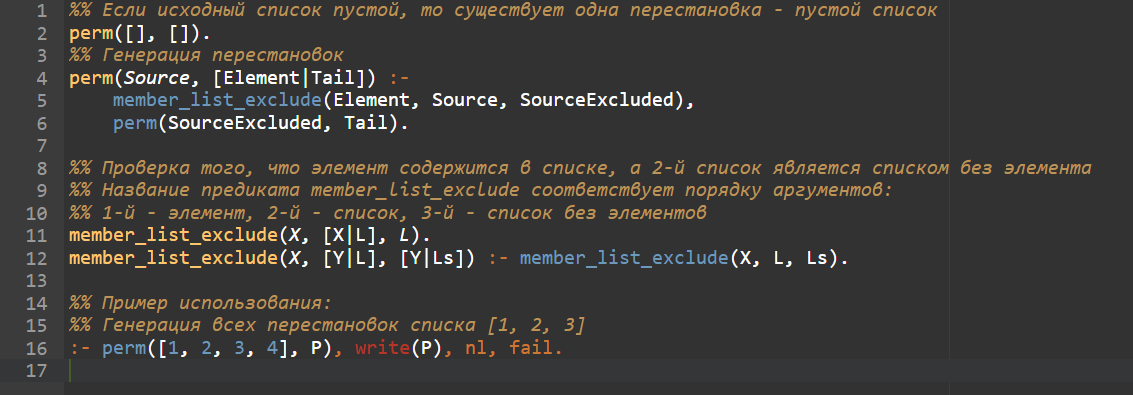 енерируем перестановки списка [1, 2, 3].

Р исунок 3

Рисунок 4

Этот код позволяет генерировать все перестановки элементов списка. Вызов perm([1, 2, 3], P) сгенерирует и выведет все перестановки элементов списка [1, 2, 3].

3 задача: написать программу, которая бы генерировала сочетания.

Код программы

%% Предикат member(X, L) проверяет принадлежность элемента X списку L

member(X, [X|_]).

member(X, [_|L]) :- member(X, L).

%% Генерация сочетаний

comb([], []).

%% Вариант 1: 1-й элемент сочетания содержится в исходном списке

comb([X|List], [X|Tail]) :- comb(List, Tail).

%% Вариант 2: сочетание является правильным сочетанием хвоста списка,

%% то есть 1-й элемент исходного списка не содержится в сочетании

comb([_|List], Tail) :- comb(List, Tail).

%% Генерация всех сочетаний для списка [1, 2, 3]

:- comb([1, 2, 3], C), write(C), nl, fail.

Результат работы

Г енерируем перестановки сочетания [1, 2, 3].

Рисунок 5

Рисунок 6

Этот код позволяет генерировать все сочетания элементов списка. Вызов comb([1, 2, 3], C) сгенерирует и выведет все сочетания элементов списка [1, 2, 3].

4 задача: написать программу, которая бы реализовывала наивную сортировку.

Код программы

%% Наивная сортировка списка

sort([], []).

sort(List, [Min|SortRest]) :-

min_list_exclude(Min, List, Exclude),

sort(Exclude, SortRest).

%% Рекурсивное исключение минимального элемента из списка

min_list_exclude(M, [M], []).

min_list_exclude(Min, [M|L], ExcludeRes) :-

min_list_exclude(Ms, L, Exclude),

find_result(M, Ms, M, L, Min, ExcludeRes).

%% Поиск минимального элемента в списке и формирование результата

find_result(M, Ms, M, L, M, L):- M < Ms.

find_result(M, Ms, Ms, Exclude, Min, Exclude):- Ms =< M.

%% Сортировка списка [3, 1, 4, 1, 5, 9, 2, 6]

:- sort([3, 1, 4, 1, 5, 9, 2, 6], Sorted), write(Sorted), nl.

Результат работы

С овершаем наивную сортировку списка [3, 1, 4, 1, 5, 9, 2, 6].

Р исунок 7

Рисунок 8

При каждом шаге алгоритм находит минимальный элемент в списке и добавляет его в отсортированный список, исключая его из оригинального. Затем процесс повторяется с оставшимися элементами, пока список не будет полностью отсортирован.

5 задача: написать программу, которая бы реализовывала быструю сортировку.

Код программы

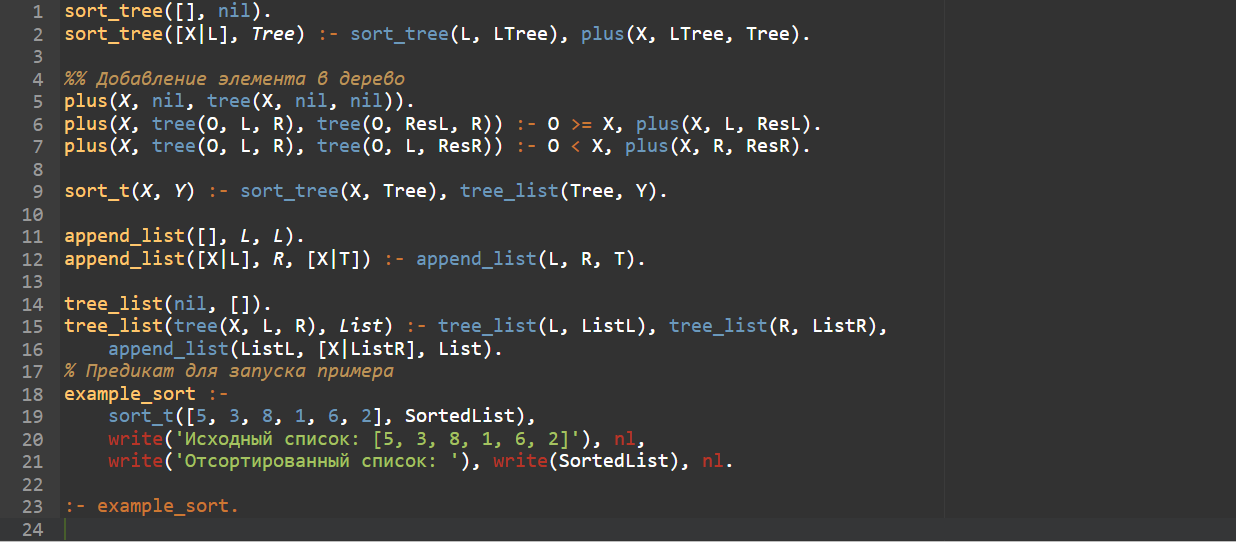
sort_tree([], nil).

sort_tree([X|L], Tree) :- sort_tree(L, LTree), plus(X, LTree, Tree).

%% Добавление элемента в дерево

plus(X, nil, tree(X, nil, nil)).

plus(X, tree(O, L, R), tree(O, ResL, R)) :- O >= X, plus(X, L, ResL).

plus(X, tree(O, L, R), tree(O, L, ResR)) :- O < X, plus(X, R, ResR).

sort_t(X, Y) :- sort_tree(X, Tree), tree_list(Tree, Y).

append_list([], L, L).

append_list([X|L], R, [X|T]) :- append_list(L, R, T).

tree_list(nil, []).

tree_list(tree(X, L, R), List) :- tree_list(L, ListL), tree_list(R, ListR),

append_list(ListL, [X|ListR], List).

% Предикат для запуска примера

example_sort :-

sort_t([5, 3, 8, 1, 6, 2], SortedList),

write('Исходный список: [5, 3, 8, 1, 6, 2]'), nl,

write('Отсортированный список: '), write(SortedList), nl.

:- example_sort.

Результат работы

Р еализуем быструю сортировку списка [5, 3, 8, 1, 6, 2].

Р исунок 9

Рисунок 10

Этот код позволяет реализовать быструю сортировку на основе деревьев.

Вывод:

В ходе выполнения лабораторной работы были получены навыки для работы на Прологе и реализованы задачи поиска совершенных чисел, генерации перестановок и сочетаний, наивной и быстрой сортировки.