Министерство науки и образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Уфимский университет науки и технологий»

Кафедра вычислительной математики и кибернетики

ОТЧЁТ

По лабораторной работе №2

«ПАРАЛЛЕЛЬНОЕ ВЫЧИСЛЕНИЕ ПРОИЗВЕДЕНИЯ ДВУХ МАТРИЦ СРЕДСТВАМИ OPENMP»

по дисциплине «Параллельные вычисления»

Выполнили:

студенты группы ПРО-429

Ихсанова Э. А., Видманов А. А.,

Мустафин А.А.

Проверила:

проф. каф. ВМИК,

канд. физ.-мат. наук Шерыхалина Н.М.

Уфа — 2024 г.

Цель работы

Приобрести навыки распараллеливания вложенных циклов с использованием директив OpenMP. Исследовать ускорение, эффективность и производительность многопоточных реализаций алгоритмов решения задачи матричного умножения.

Ход работы

Мы написали код последовательной программы перемножения матриц, по заданию было необходимо ее распараллелить, реализовывав три алгоритма.

Было подобрано значение q = 1700, N = 100, при этом время работы составило 10.042

Используя интерфейс OpenMP можно распределить между потоками итерации любого из этих циклов.

Пусть для определенности внешнему циклу соответствует счетчик і,

среднему - j, а внутреннему - k. Тогда распараллеливание внутреннего цикла будет соответствовать алгоритму 1, то есть вычисление суммы по k из

будет распределено по потокам, в результате чего над вычислением каждого элемента будут параллельно работать все потоки.

Для 1-го алгоритма распараллеливания было необходимо распараллелить k-ый цикл:

Распараллеливание среднего цикла (по j) соответствует алгоритму 2, то есть осуществляется столбцевая декомпозиция матрицы С.

Для 2-го – j-ый:

Наконеw, распараллеливание внешнего цикла (по і) приводит к алгоритму 3, когда имеет место строковая декомпозиция матрицы С.

Для 3-го – i-ый

Сравнив время работы каждой из программы, мы пришли к выводу, что. самым эффективным является 3-й алгоритм.

Сравнили значения времени последовательной работы программы и при параллельной ее версии:

N	q(кол-во матричных умножений)	T1	Tp
5	14000000	10,314	30,303
10	1700000	10,009	11,123
50	14000	10,404	5,651
100	1700	10,075	4,607
200	210	10,09	4,33
500	13	10,03	4,281

Вычислили ускорение и эффективность для каждого N:

N	S	E
5	0,3403623	0,08509059
10	0,8998472	0,22496179
50	1,8410901	0,46027252
100	2,1868895	0,54672238
200	2,330254	0,58256351
500	2,3429105	0,58572763

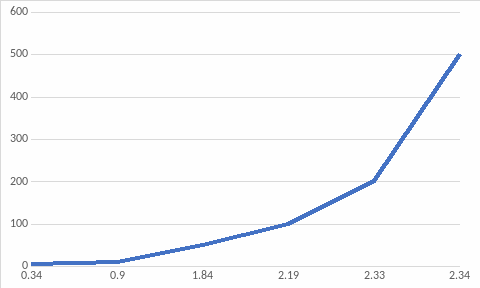
Построили график зависимости ускорения параллельной программы от размерности умножаемых матриц и пришли к выводу, что чем больше размерность матриц тем больше ускорение параллельной программы:

П иковая производительность системы:

4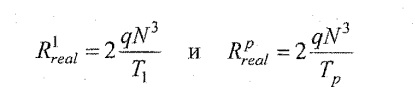 * 3,2 *10^9 * 2,6 = 33,28^9 = 33280000000

N	R1real	Rpreal	U1	Up
5	339344580	115500116	0,01019665	0,00347056
10	339694275	305672930	0,01020716	0,00918488
50	336409073	619359405	0,01010845	0,01861056
100	337468983	738007380	0,01014029	0,0221757
200	333002973	775981524	0,0100061	0,02331675
500	324027916	759168419	0,00973642	0,02281155

Вывод

В ходе выполнения лабораторной работы мы приобрели навыки распараллеливания вложенных циклов с использованием директив OpenMP. Исследовали ускорение, эффективность и производительность многопоточных реализаций алгоритмов решения задачи матричного умножения. Пришли к выводу о том, что чем больше выбранная в программе размерность матриц, тем более эффективно работает распараллеливание программы.