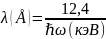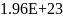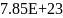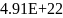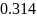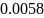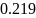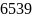идз / ИДЗ1 Андреева
.docxМИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра микро- и наноэлектроники |
||||||
ОТЧЁТ по индивидуальному домашнему заданию № 1 по дисциплине «Методы анализа структур электроники и микросистемной техники» Тема: Моделирование рентгеновского спектра заданного образца
|
||||||
|
||||||
Санкт-Петербург 2025 |
МОДЕЛИРОВАНИЕ СПЕКТРА
Исследуемый
образец – Mn2O4Ti.
В таблице 1 приведём значения энергии
связи
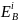 электронов на i-ом
слое для атомов, содержащихся в исследуемом
образце.
электронов на i-ом
слое для атомов, содержащихся в исследуемом
образце.
Таблица 1 – Энергии связи электронов в атомах образца, еВ
Z |
М, г/моль |
Элемент |
K |
LI |
LII |
LIII |
MI |
MII |
MIII |
MIV |
MV |
25 |
54,938 |
Mn |
6539 |
769 |
652 |
641 |
84 |
49 |
4 |
||
8 |
16 |
O |
532 |
24 |
7 |
– |
– |
– |
– |
– |
|
22 |
47,9 |
Ti |
4965 |
564 |
461 |
455 |
59 |
34 |
3 |
||
Для ионизации всех К-оболочек достаточно энергии Е0 = 10 кэВ, возьмём это значение как энергию зонда. При этом будем наблюдать следующие переходы:
Kα: K→LⅢ
Kβ: K→MⅢ
Lα: LⅢ→MⅤ
Lβ: LⅡ→MⅣ
Энергии квантов характеристического рентгеновского излучения элементов образца рассчитываются по формулам (1) − (4).
|
(1) |
|
(2) |
|
(3) |
|
(4) |
В таблице 2 приведём расчёт значений энергии квантов характеристического рентгеновского излучения в спектре.
Таблица 2 – Положение по энергии линий характеристического рентгеновского излучения в спектре, эВ
Элемент |
|
|
|
|
Mn |
5898 |
6490 |
637 |
648 |
O |
525 |
– |
– |
– |
Ti |
4510 |
4931 |
452 |
458 |
Пример расчёта для титана (Ti):
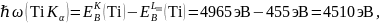
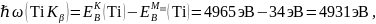
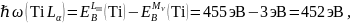
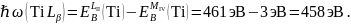
На рисунке 1 качественно изобразим спектр исследуемого образца.
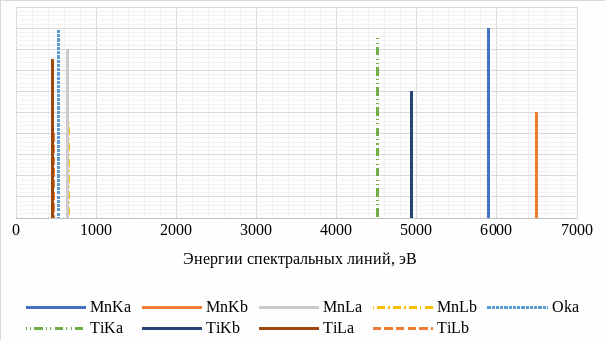
Рисунок 1 – Качественный рентгеновский спектр
Из-за ограничений по разрешению энергетического спектра в спектроскопии с дисперсией по энергии (150 эВ) некоторые спектральные линии будут сливаться в одну детектируемую спектрометром линию – в данном случае это MnLα-линия и MnLβ-линия, OKα-линия, TiLα-линия, и TiLβ-линия.
Так как среди этих линий есть линия кислорода, необходимая нам для детектирования, мы не можем убрать их из рассмотрения. Соответственно, необходимо использовать спектрометрию с волновой дисперсией.
В спектрометрии с волновой дисперсией также есть ограничения по разрешению энергетического спектра (10 эВ), некоторые спектральные линии также будут сливаться в одну детектируемую спектрометром линию: TiLα-линия, и TiLβ-линия.
Для
детектирования всех элементов остаётся
достаточно энергии электронного зонда
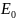 ,
равной 10 кэВ.
,
равной 10 кэВ.
Для расчёта выхода характеристического рентгеновского излучения используем соотношение (5).
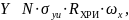 (5)
(5)
где
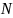 – атомный процент содержания элемента,
– атомный процент содержания элемента,
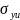 – сечение
ударной ионизации, определяемое
соотношением (6),
– сечение
ударной ионизации, определяемое
соотношением (6),
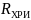 – радиус
сферы генерации характеристического
рентгеновского излучения, определяемый
соотношением (7),
– радиус
сферы генерации характеристического
рентгеновского излучения, определяемый
соотношением (7),
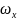 – выход
флюоресценции, справочное значение.
– выход
флюоресценции, справочное значение.
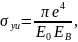 (6)
(6)
где
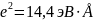 .
.
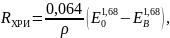 (7)
(7)
где
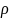 – плотность соединения, определяемая
соотношением (8).
– плотность соединения, определяемая
соотношением (8).
|
(8) |
где n – количество формульных единиц в единице объёма,
М – молярная масса одной формульной единицы,
NA = 6,02∙1023 моль-1 – число Авогадро.
Для того, чтобы найти количество формульных единиц в единице объёма, необходимо найти объём ячейки. В нашем случае решётка имеет тетрагональную сингонию, как видно на рисунке 2, соответственно объём можем найти по формуле (9).
|
(9) |
где 𝑎 = 6,17 Å,
c = 8,564 Å.
Число формульных единиц на одну ячейку равно 4. Тогда количество формульных единиц в единице объёма будет определяться выражением (10).
|
(10) |
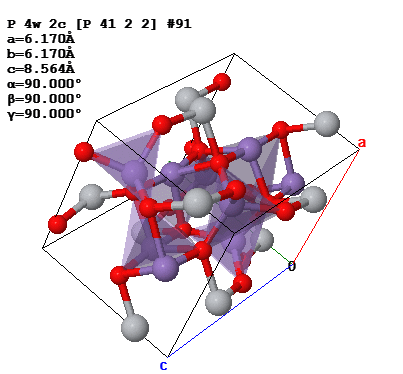
Рисунок 2 – Элементарная ячейка Mn2O4Ti
Молярная масса одной формульной единицы рассчитывается по формуле (11):
|
(11) |
где M𝑖 – молярная масса i-го элемента.
Произведём расчёт плотности соединения:
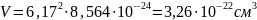
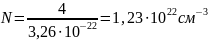
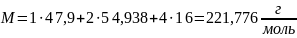
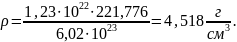
Количество атомов элемента в единице объёма можно найти как произведение количества формульных единиц в единице объёма на количество атомов элемента в одной формульной единице. Произведём расчёт для каждого элемента.
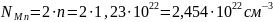
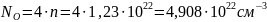
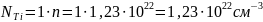
В спектрометрии с волновой дисперсией основной характеристикой спектральной линии является длина волны λ. Для этого значения энергий спектральных линий из таблицы 2 переведём в значение длин волн по формуле (12) и запишем полученные значения в таблицу 3.
|
(12) |
Таблица 3 – Положение по длине волны линий характеристического рентгеновского излучения в спектре, Å
Элемент |
|
|
|
|
Mn |
2,10 |
1,91 |
19,47 |
19,14 |
O |
23,62 |
– |
– |
– |
Ti |
2,75 |
2,51 |
27,43 |
27,07 |
Выбор аналитических линий обусловливается яркостью, возможностью регистрации на конкретном спектрометре, а также возможностью возбуждения. В данной работе в качестве аналитических были выбраны следующие линии: MnKα, OKα, TiKα.
Полученные расчётные данные для сечения ударной ионизации, радиуса сферы генерации характеристического рентгеновского излучения и интенсивности спектральной линии укажем в таблице 4. На рисунке 3 построим нормированный модельный спектр исследуемого образца.
Пример расчёта для Kα титана (Ti):
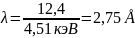
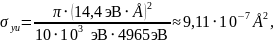
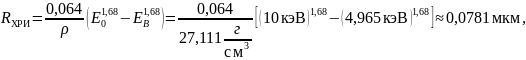
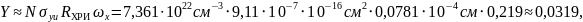
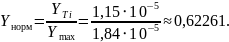
Таблица 4 – Параметры модельного рентгеновского спектраXспектральная линия |
MnKa |
Oka |
TiKa |
||
атомов на эл ячейку |
8 |
16 |
4 |
||
n, 1/см^3 |
2.45E+22 |
4.91E+22 |
1.23E+22 |
||
N,частиц/см^3 |
|
|
|
||
ρ, г/см^3 |
9.037 |
18.074 |
4.518 |
||
Re, мкм |
0.172928 |
0.168259 |
0.468851 |
||
ωx |
|
|
|
||
Eв, эВ |
|
|
|
||
σун, Å^2 |
6.92E-07 |
8.5E-06 |
9.11E-07 |
||
интенсивность |
7.37E-05 |
6.52E-05 |
4.59E-05 |
|
|
нормированная интенсивность |
1 |
0.883633 |
0.62261 |
|
|
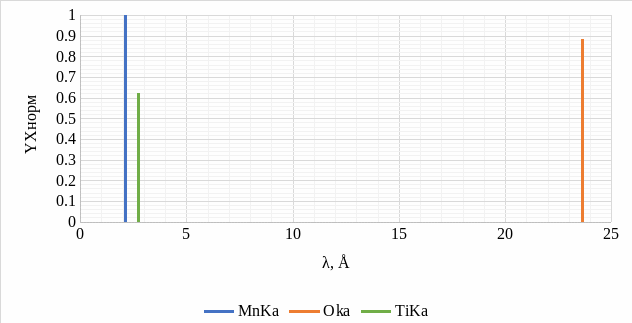
Рисунок 3 – Модельный спектр исследуемого образца

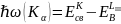
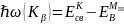
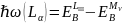
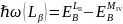
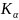
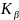
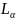
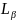
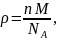
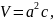
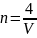
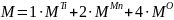 ,
,