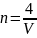идз / ИДЗ3 Андреева

МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра микро- и наноэлектроники

отчет по индивидуальному домашнему заданию № 3 по дисциплине «Методы анализа структур электроники и микросистемной техники» Тема: «Рентгеновская фотоэлектронная спектроскопия»

Студентка гр. 1283 ____________________ Григорьева. В.В. Преподаватель __________________________ Андреева Н.В.

Санкт-Петербург 2025

МОДЕЛИРОВАНИЕ СПЕКТРА

Исследуемый образец – Mn₂O₄Ti. В таблице 1 приведём значения энергии связи 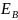электронов, содержащихся в исследуемом образце.

Таблица 1 – Энергии связи электронов для различных оболочек атомов, входящих в состав образца, эВ

Z	М, г/моль	Элемент	Оболочка
			1s1/2	2s1/2	2p1/2	2p3/2	3s1/2	3p1/2	3p3/2	3d3/2	3d5/2
25	54,938	Mn	6539	769	652	641	84	49		4
8	16	O	532	24	7		–	–	–	–	–
22	47,9	Ti	4965	564	461	455	59	34		3

В качестве источника излучения возьмём мишень Mg:

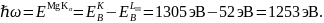
В таблице 2 приведём значения энергии фотоэлектронов.

Таблица 2 – Кинетические энергии фотоэлектронов, эВ

Элемент	Оболочка
	1s1/2	2s1/2	2p1/2	2p3/2	3s1/2	3p1/2	3p3/2		3d3/2	3d5/2
Mn	–	484	601	612	1169	1204		1249
O	721	1229	1246		–	–	–		–	-
Ti	–	689	792	798	1194	1219		1250

Пример расчёта для фотоэлектрона на уровне 2s_1/2 атома Mn:

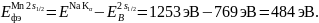
На рисунке 1 изобразим качественный обзорный РФЭ-спектр исследуемого образца.

Из-за ограничений по разрешению энергетического спектра (10 эВ) некоторые спектральные линии будут сливаться в одну детектируемую спектрометром линию – в данном случае это: Ti_2p1/2-линия и Ti_2p3/2-линия, Mn_3d-линия, O_2p-линия, и Ti_3d-линия.

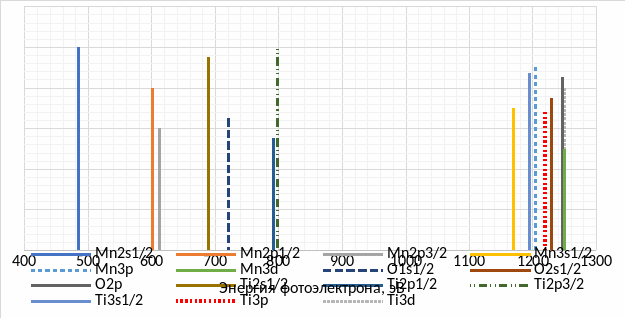
Рисунок 1 – Качественный рентгеновский спектр

Для всех значений энергий фотоэлектронов проведём расчет сечения фотоионизации, используя соотношение (1). Данные приведём в таблице 3.

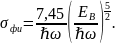(1)

Таблица 3 – Сечение фотоионизации, Ų

Элемент

Оболочка

1s1/2

2s1/2

2p1/2

2p3/2

3s1/2

3p1/2

3p3/2

3d3/2

3d5/2

Mn

–

0,00175

0,00116

0,00111

6,9⋅10-6

1,8⋅10-6

3,4⋅10-9

O

0,0007

3⋅10-7

1,4⋅10-8

–

–

–

–

–

Ti

–

0,00081

0,00049

0,00047

2,9⋅10-6

7,2⋅10-7

1,7⋅10-9

Пример расчёта для уровня 2s_1/2 атома Mn:

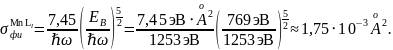
Для того, чтобы найти количество формульных единиц в единице объёма, необходимо найти объём ячейки. В нашем случае решётка имеет тетрагональную сингонию, как видно на рисунке 2, соответственно объём можем найти по формуле (2).

(2)

где 𝑎 = 6,17 Å,

c = 8,564 Å.

Число формульных единиц на одну ячейку равно 4. Тогда концентрация формульных единиц в единице объёма будет определяться выражением (3).

(3)

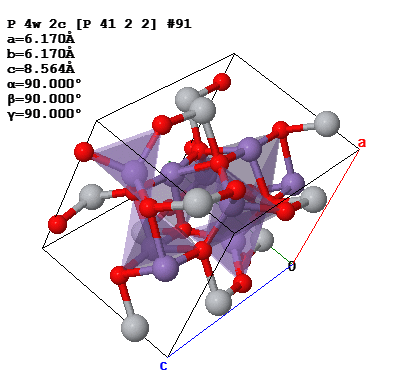
Рисунок 2 – Элементарная ячейка Ti₂O₄Ti

Произведём расчёт:

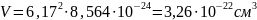
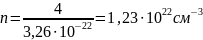
Количество атомов элемента в единице объёма можно найти как произведение количества формульных единиц в единице объёма на количество атомов элемента в одной формульной единице. Произведём расчёт для каждого элемента.

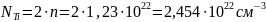
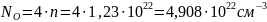
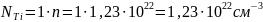
Проведем расчет интенсивности спектральных линий, используя соотношение (4). Расчет представим в таблице 4. Спектр представим на рисунке 3, причём изобразим только самые интенсивные линии для каждого из элементов соединения.

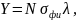(4)

Длину свободного пробега найдём по универсальной кривой, где энергии сопоставим энергиям фотоэлектрона, представленным в таблице 2.

Таблица 4 – Расчет интенсивности

	N,см-3	σфи, Å^2	Ефэ, эВ	λ, Å	Y	Yнорм
Mn2s1/2	2,45⋅1022	1,75⋅10-3	484	10	4,31⋅10-4	0,739
O1s1/2	4,91⋅1022	6,98⋅10-4	721	17	5,83⋅10-4	1
Ti2s1/2	1,23⋅1022	8,08⋅10-4	689	16,5	1,64⋅10-4	0,281

Пример расчёта для Mn2s1/2:

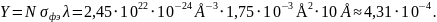
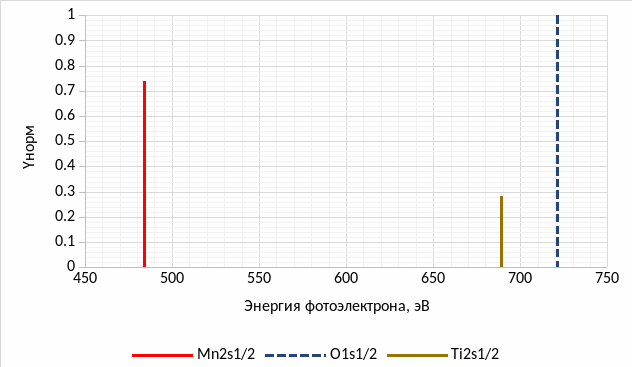
Рисунок 3 – Нормированный спектр