Курсовая работа 2 сем / Элтех курсовая 1 вариант 21
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра
Теории электрических цепей
КУРСОВАЯ РАБОТА
по дисциплине
ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Задача 1
«Расчет разветвленных цепей»
Студент:
Группа: БИК
Преподаватель:
Москва г.
ЗАДАНИЕ №1
1. Расчет резистивных цепей постоянного тока
1.1. Перечертите для вашего варианта N исходную схему и рассчитайте параметры её элементов по формулам:
Е1 = 10 + N В; Е2 = 5 + N B; J=N/10 А;
R1 = 1 + N Ом; R2 = 2 + N Oм; R3 = 3 + N Oм; R = 4 + N Ом;
N = 21 - номер варианта
1.2. Методом уравнений Кирхгофа определить
токи во всех ветвях.
1.3. Методом контурных токов определить токи во
всех ветвях.
1.4. Методом узловых потенциалов определить токи
во всех ветвях.
1.5. Методом двух узлов определить токи во всех ветвях.
1.6. Методом наложения определить токи во всех ветвях.
1.7. Рассчитать ток в сопротивлении R1 методом эквивалентного генератора ЭДС.
1.8. Рассчитать ток в сопротивлении R2 методом эквивалентного
генератора тока.
1.9. Рассчитать баланс мощностей для исходной схемы. Проверить баланс мощностей с помощью ЭВМ, например программ МіcroСар или Circuit Maker.
Параметры элементов схемы:
N = 21
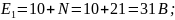
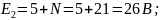

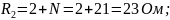
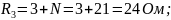
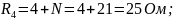
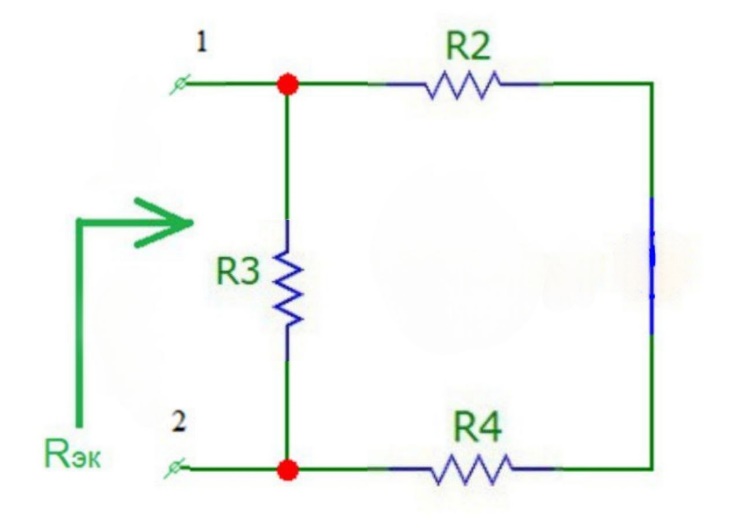
Исходная схема представлена на рис.1:
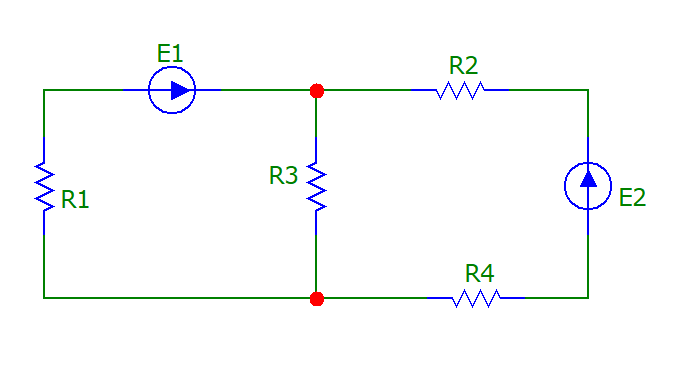
Рисунок 1
Метод уравнения Кирхгофа
Используя метод уравнений Кирхгофа, определим токи во всех ветвях. Для применения этого метода необходимо произвольно задать направление токов во всех ветвях, что представлено на рис.2:


Рисунок 2
Далее, выбираем произвольные положительные направления токов во всех ветвях и вычисляем необходимое количество уравнений, основываясь на первом и втором законах Кирхгофа:
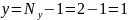
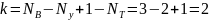
Запишем уравнение по 1-ому закону Кирхгофа:
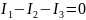
Для записи уравнений по второму закону Кирхгофа произвольно выбираем первый контур и в нем произвольно задается направление обхода контура. Затем, из цепи в уме удаляется какая-либо ветвь, и снова задается направление обхода для оставшегося участка.
По второму закону Кирхгофа:

Представим систему в матричном виде:

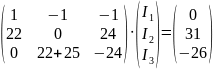
или
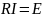
Находим токи:
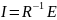
Вычисление было произведено с помощью программы Mathcad:
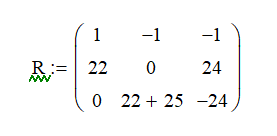
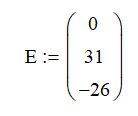
![]()
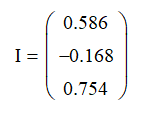
Ответ:
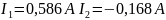
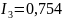 А
А
Метод контурных токов
С помощью метода контурных токов определим токи во всех ветвях.
Произвольно выбираем направления всех токов в ветвях на исходной
схеме (рис.3)
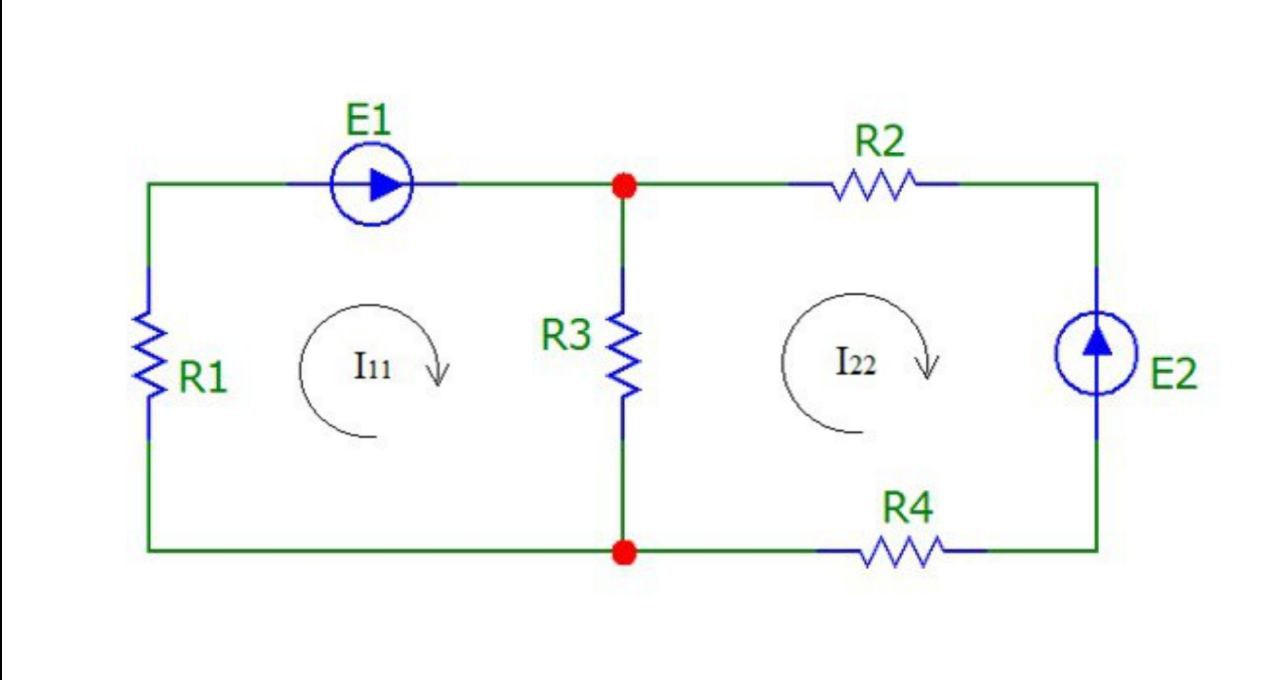
Рисунок 3
Число независимых контуров:
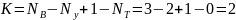
Выбираем положительные направления для контурных токов
положительные направления для контурных токов:

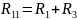
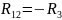
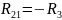
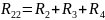
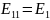
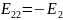
Выпишем систему уравнений:
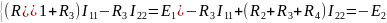
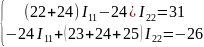
Вычисление было произведено с помощью программы Mathcad:
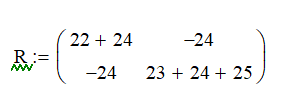

![]()
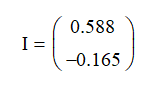
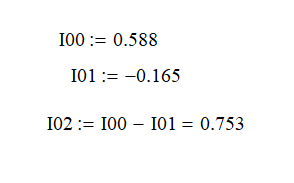
Ответ:
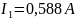

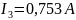
Метод узловых потенциалов
С помощью метода узловых потенциалов определим токи во всех ветвях.
Произвольно выбираем направление всех токов в ветвях на исходной схеме (рис.4)
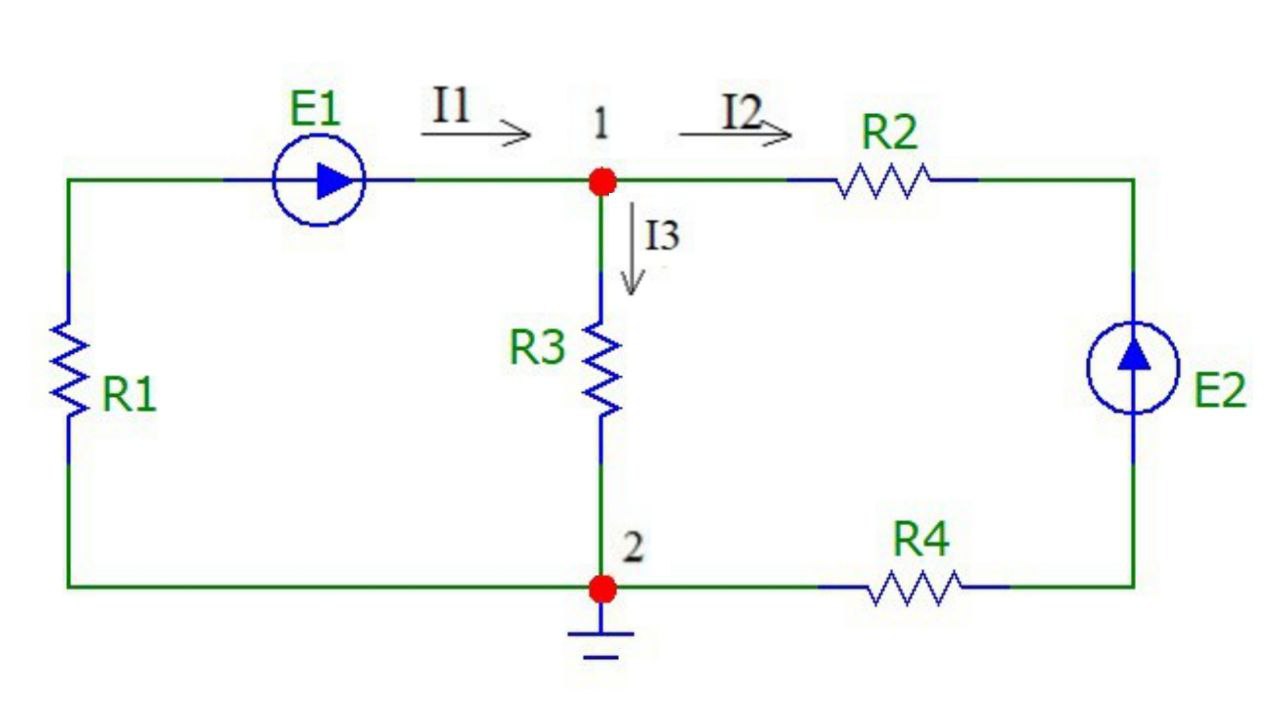
Рисунок 4
Число уравнений:
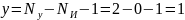
Принимаем потенциал узла 2 за ноль. Тогда уравнение для нахождения потенциала узла 1:
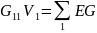
Где
 – потенциал узла 1;
– потенциал узла 1;
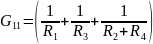 -
сумма проводимостей ветвей, сходящихся
в узле 1;
-
сумма проводимостей ветвей, сходящихся
в узле 1;
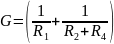 -
сумма проводимостей ветвей, непосредственно
соединяющих узел 1 с узлом 2;
-
сумма проводимостей ветвей, непосредственно
соединяющих узел 1 с узлом 2;
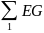 –
алгебраическая
сумма произведения ЭДС ветвей, примыкающих
к узлу 1.
–
алгебраическая
сумма произведения ЭДС ветвей, примыкающих
к узлу 1.
С помощью программы Mathcad находим:
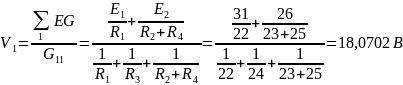
Токи в ветвях, согласно обобщенному закону Ома, при V2=0 В равны:
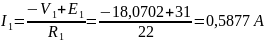
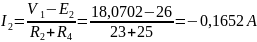
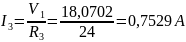
Ответ:
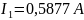
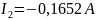
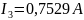
Метод двух узлов
Используя метод двух узлов, определим токи во всех ветвях. Этот метод представляет собой частный случай метода узловых потенциалов и является наиболее оптимальным для анализа цепей, содержащих два узла. Для применения метода двух узлов мы сначала определяем напряжение между этими двумя узлами (U12), а затем используем его для расчёта всех токов в ветвях. Схема, учитывающая этот метод, изображена на рис.5:
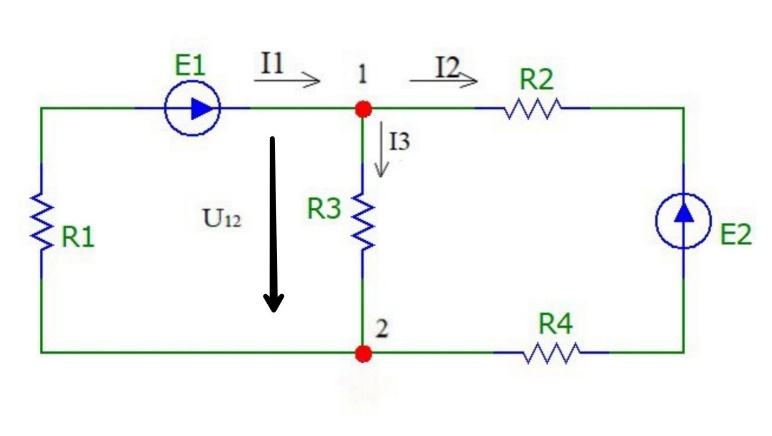
Рисунок 5
Примем потенциал узла 2 равным нулю V2=0 В. Тогда напряжение U12 будет направлено из точки с большим потенциалом, к точке с меньшим.
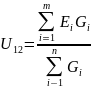
Где
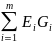 -
алгебраическая сумма произведения ЭДС
ветвей, примыкающих к узлу 1, на их
проводимости;
-
алгебраическая сумма произведения ЭДС
ветвей, примыкающих к узлу 1, на их
проводимости;
 -
алгебраическая сумма проводимостей
всех ветвей схемы.
-
алгебраическая сумма проводимостей
всех ветвей схемы.
Определяем напряжение U12 между узлами по формуле:
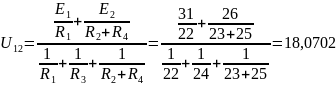 В
В
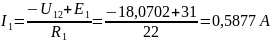
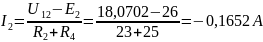
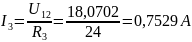
Ответ:
;
;
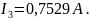
Метод наложения
Используя метод наложения, необходимо определить токи во всех ветвях. Вначале произвольно выбираем направления всех токов на исходной схеме, а затем пронумеруем все независимые источники целыми числами, как показано на рис.6

Рисунок 6
Обнулим все источники ЭДС и тока, за исключением первого. При этом, независимые источники с нулевой ЭДС заменяем короткозамкнутыми отрезками. Для удобства, частичные токи будем обозначать штрихами. Исходная схема представлена на рис.7:
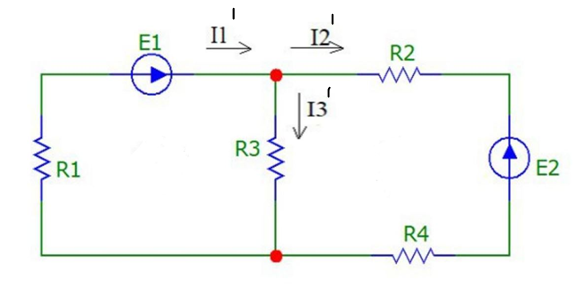
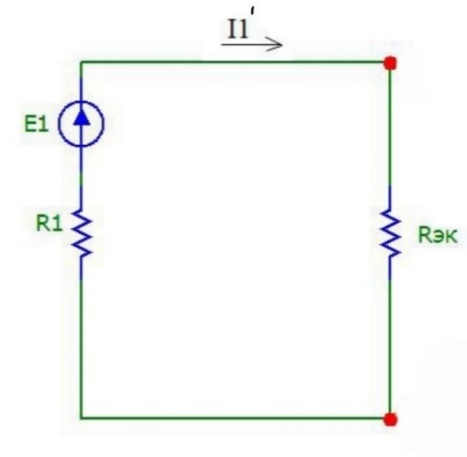
Рисунок 7
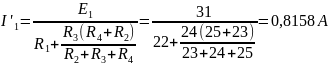
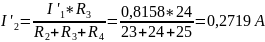
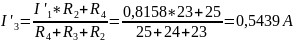
Пусть источник ЭДС E1 отключён. Метод вычисления частичных токов остаётся прежним, что продемонстрировано на рис.8:
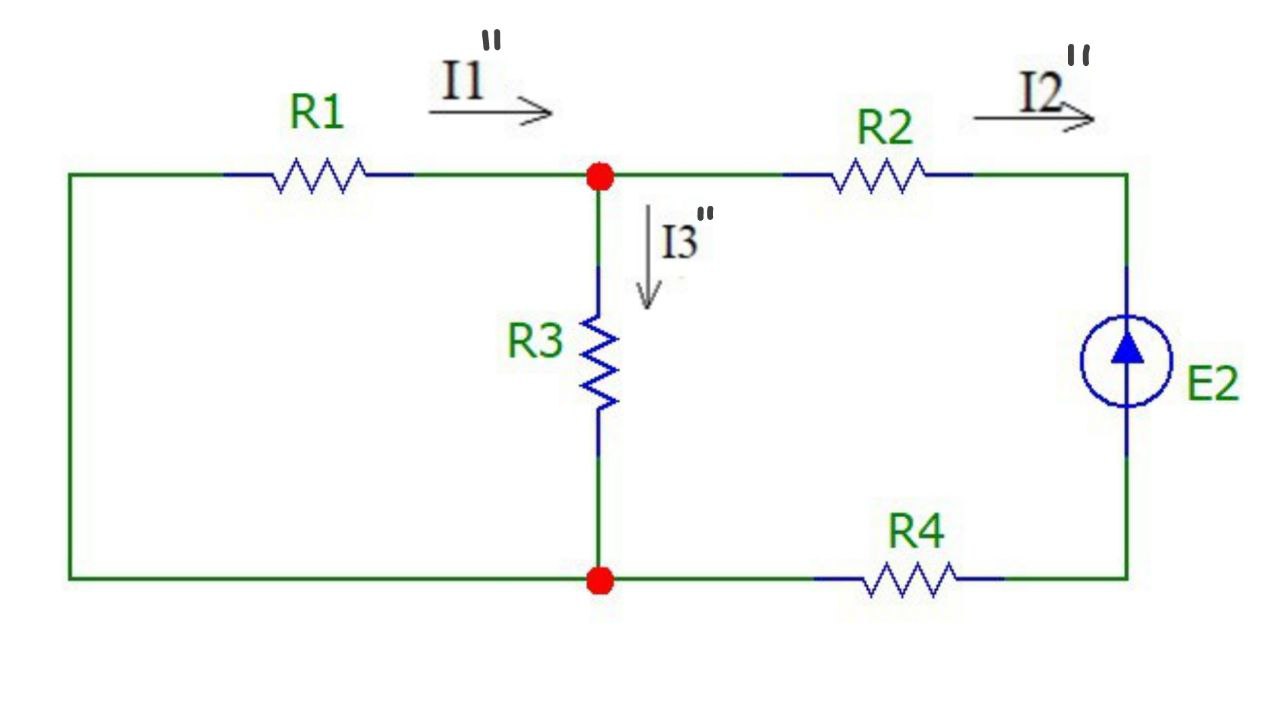
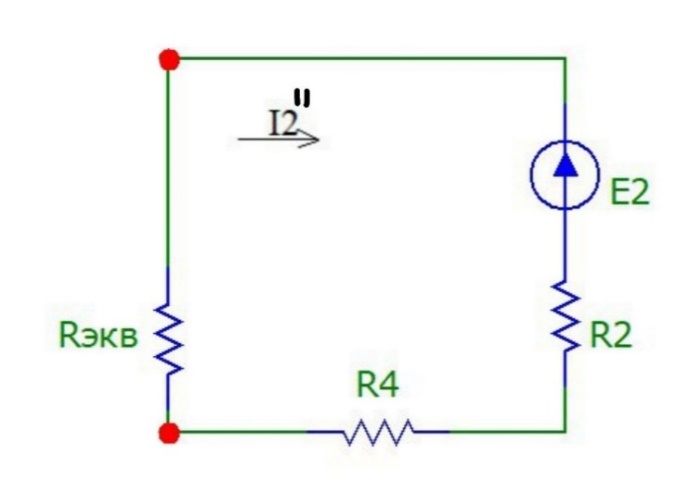
Рисунок 8
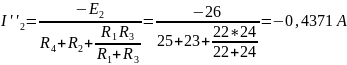
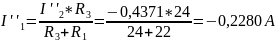
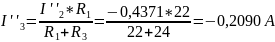
Токи ветвей находим по формулам:
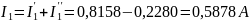
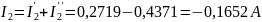
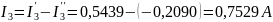
Ответ:
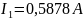
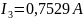
Метод эквивалентного источника ЭДС
С помощью метода эквивалентного источника ЭДС определить ток в сопротивлении R1. Произвольно выбираем направление искомого тока I в ветви на исходной схеме (рис.9):
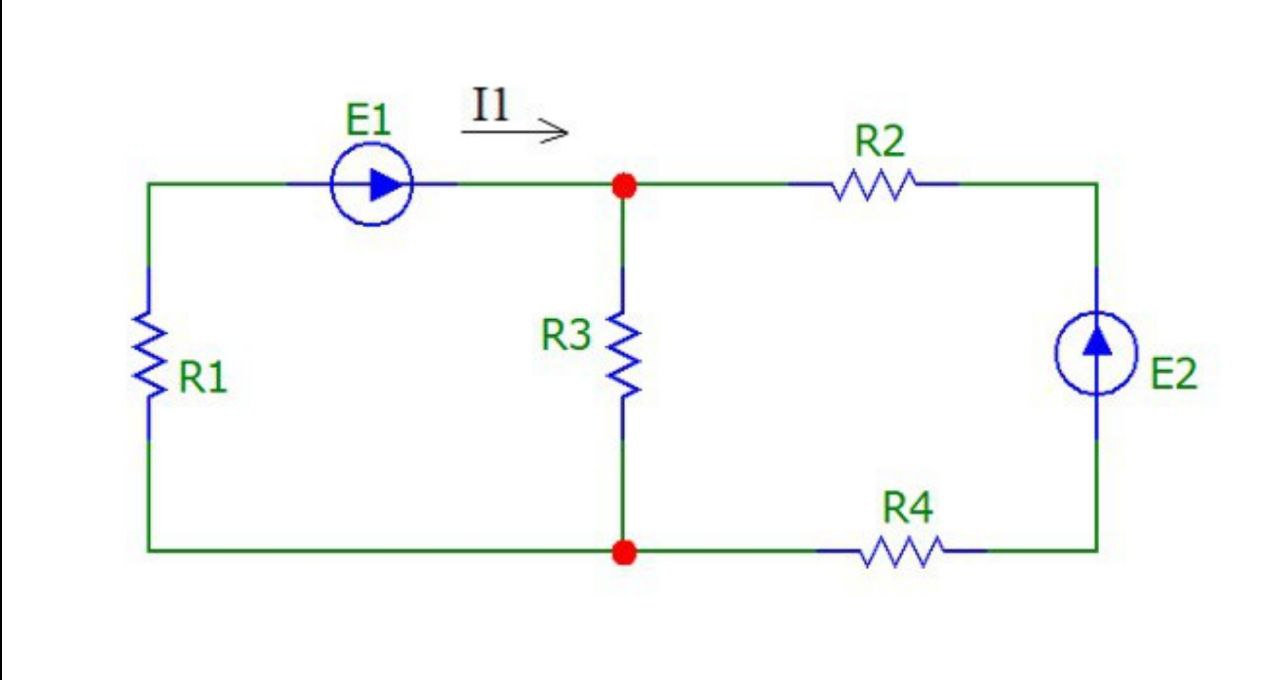
Рисунок 9
Составим схему 2, исключив ветвь из исходной схемы, и вычислим относительно зажимов 12 методом эквивалентного источника ЭДС напряжение холостого хода Uхх (рис.10):

Рисунок 10
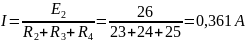
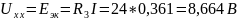
Составим схему 3 для вычисления Rэк. Для этого в схеме 2 источники ЭДС заменим короткозамкнутыми отрезками (рис.11):
Рисунок 11 |
|
Используя эквивалентные преобразования, вычислим Rэк:
С помощью программы Mathcad находим:
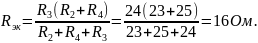
Составим одноконтурную цепь с подключенной ветвью 12, при это напряжение Eэк принять противоположным направлению Uхх на схеме 2 (рис.12):
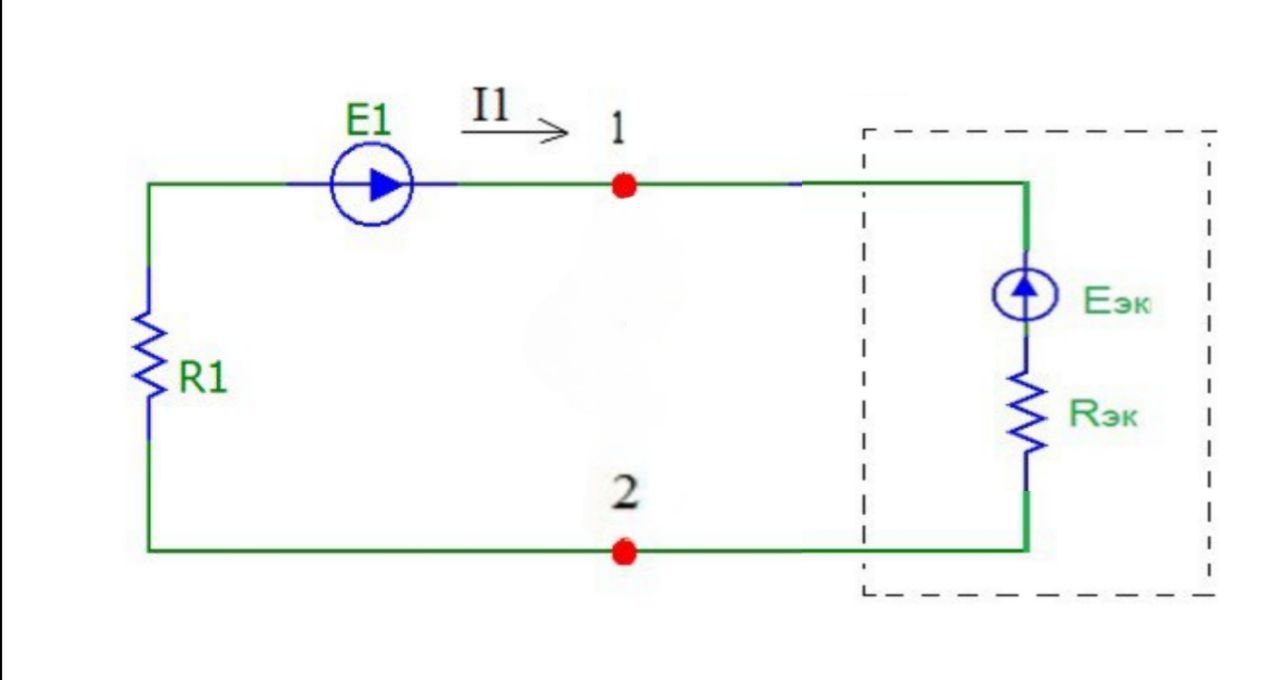
Рисунок 12
По закону Ома найдем значение искомого тока:
С помощью программы Mathcad находим:
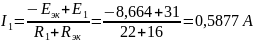
Ответ:
I1
=
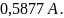
Метод эквивалентного источника тока
С помощью метода эквивалентного источника тока определим ток в сопротивлении R2. Произвольно выбираем положительное направление искомого тока I2 в ветви на исходной схеме 1 (рис. 13):
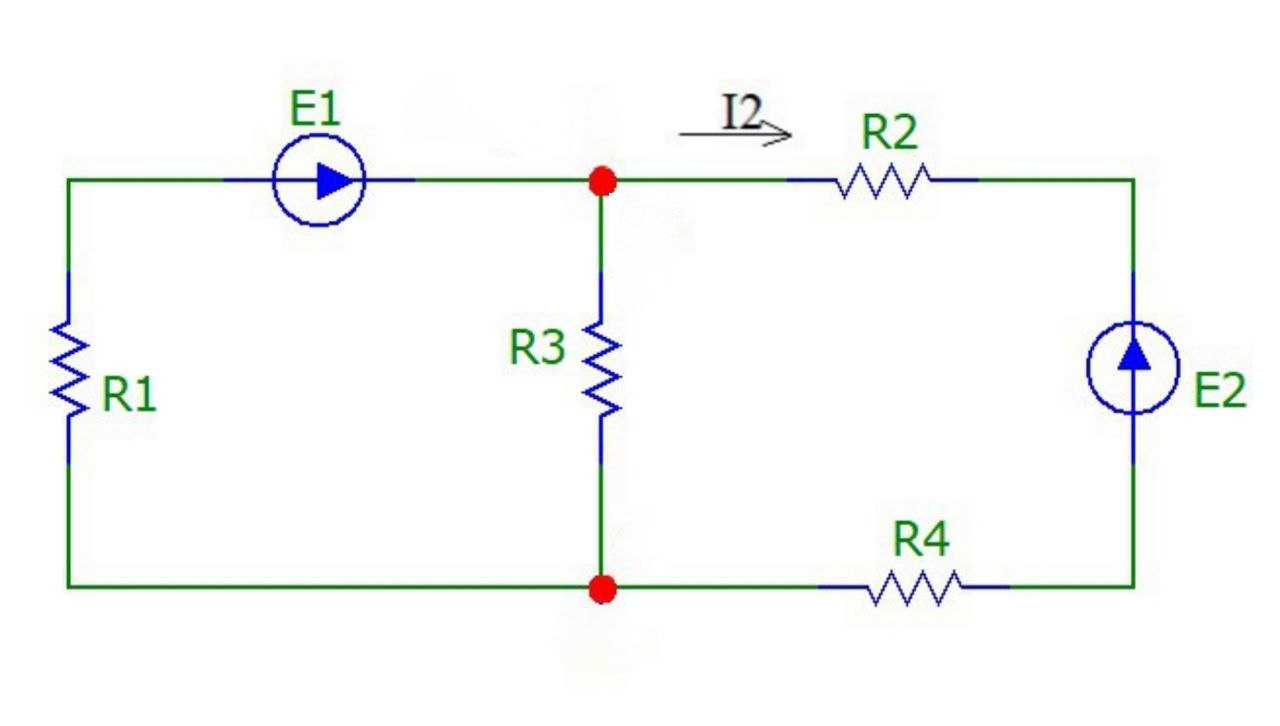
Рисунок 13
Составляем схему 2 (рис.14), заменив ветвь 12 короткозамкнутым отрезком. Направление тока короткого замыкания Ik выбираем совпадающим с направлением тока I2:
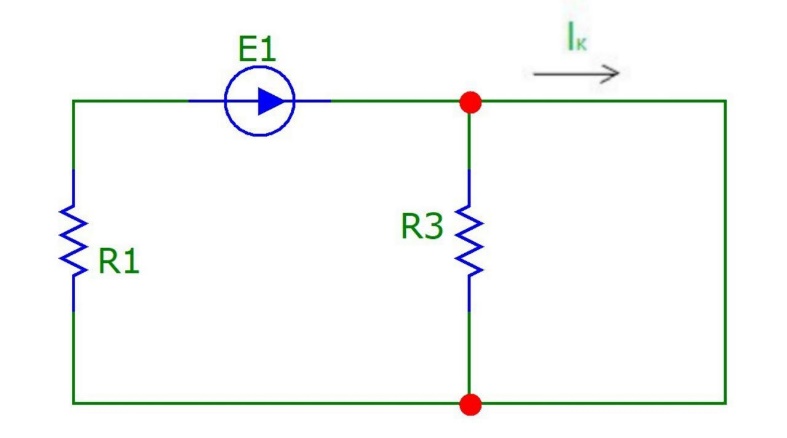
Рисунок 14
Вычисляем ток Ik:
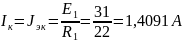
Составляем схему 3 (рис.15) для вычисления RЭК. Для этого используем схему 2, в которой источники ЭДС заменяют короткозамкнутыми отрезками:
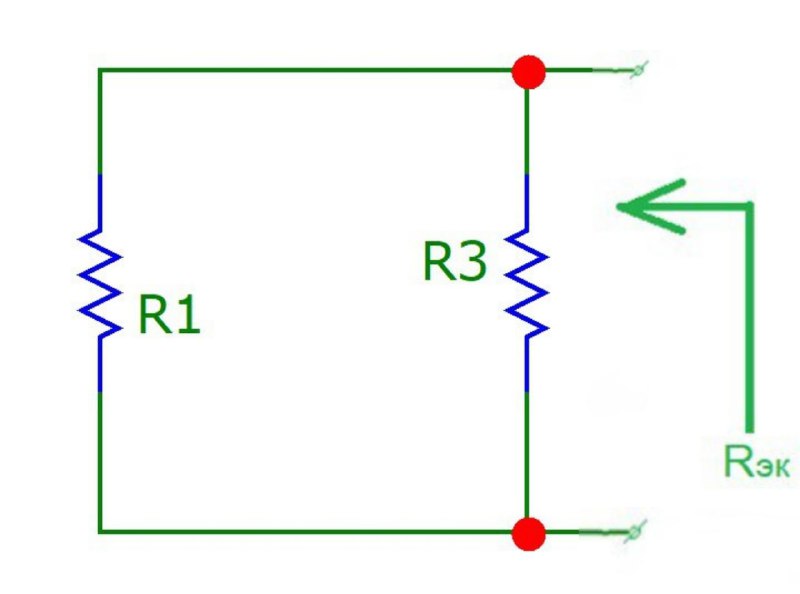
Рисунок 15
Используя эквивалентные преобразования, вычисляем RЭК относительно зажимов:
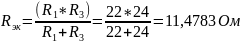
Составим цепь (рис.16) с подключенной ветвью 12. При этом направление JЭК на схеме 4 должно быть противоположным направлению Ik в схеме 2.
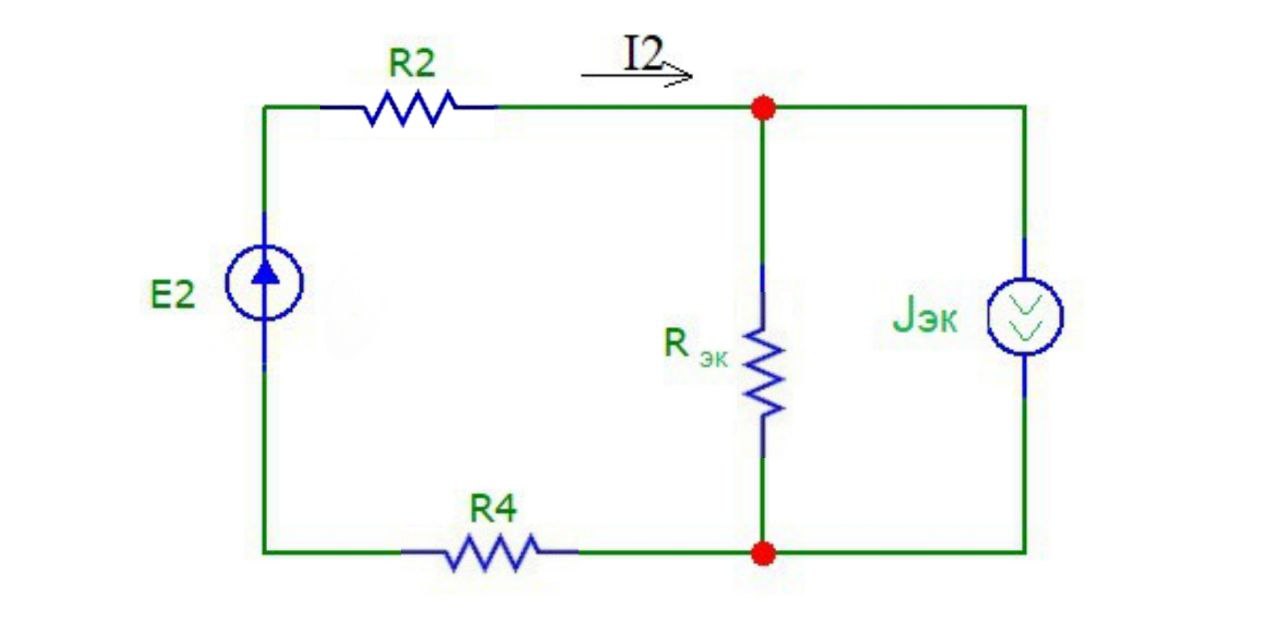
Рисунок 16
Используем метод уравнений Кирхгофа, находим искомый ток:
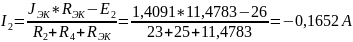
Ответ:
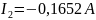
Баланс мощностей
Исходная электрическая цепь представлена на рис.17:
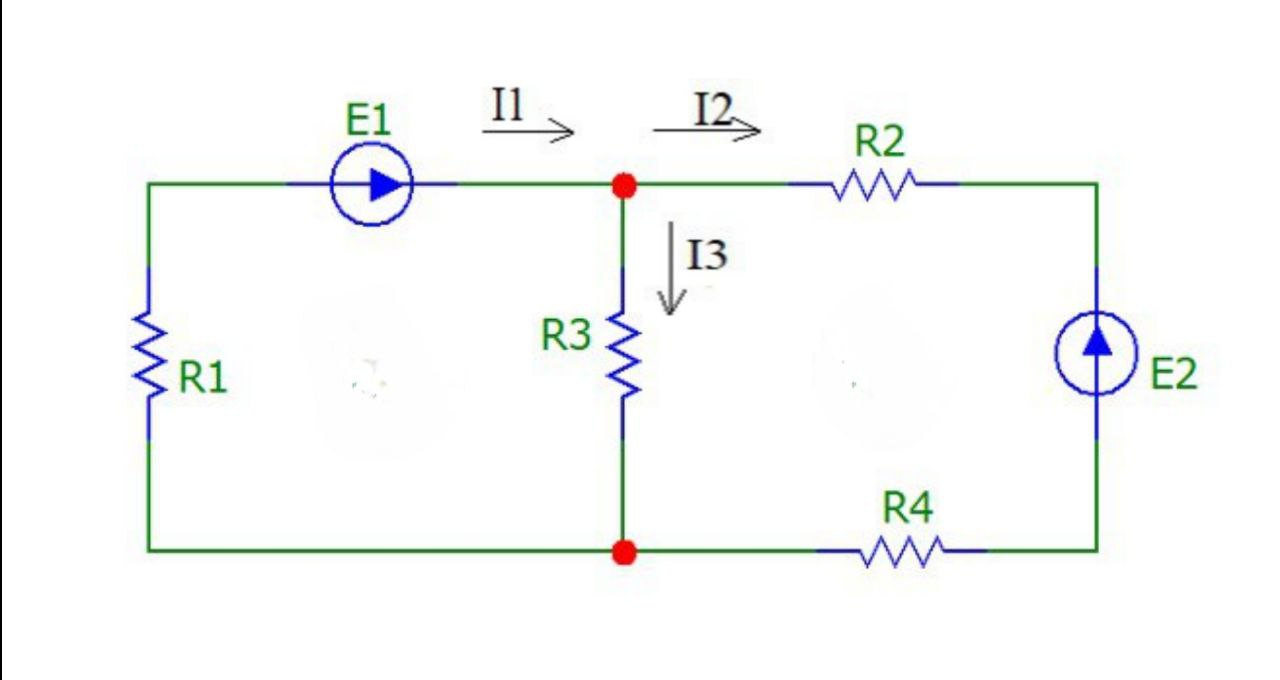
Рисунок 17
Найдем мощность источников по формуле с помощью программы Mathcad:
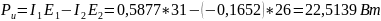
Вычислим мощность, расходуемую в приемниках по формуле:
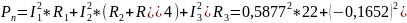
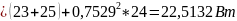
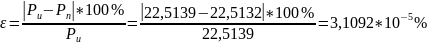
Баланс
сошелся с точность
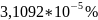 .
.
Ответ пришлось немного подгонять, но вроде как +- всё верно должно быть