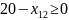УБТС ИДЗ №4

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра Биотехнических систем

индивидуальное домашнее задание

по дисциплине «Управление в биотехнических системах»

Тема: Линейное программирование. Игровые задачи

Вариант 18

Задание 4

Студентки гр. 1502		Титова В.Д.
Преподаватель		Корнеева И.П.

Санкт-Петербург

2024

Задача 1.

Для лечения трех групп больных B₁, B₂, B₃ применяются два медикаментозных препарата A₁ и A₂. Так как общее число доз этих препаратов равно общему числу больных, то каждому больному может быть выдана только одна доза какого-то из этих двух лекарств. Число больных в группе B_j равно N_j. Число доз препарата A_i равно K_i. Очевидно, что (N₁+N₂+N₃)=(K₁+K₂).

Эффективность лечения больного типа B_j препаратом A_i равна C_ij. Пусть X_ij - число больных группы B_j, получающих препарат A_i. Нужно распределить дозы препарата по больным так, чтобы суммарная эффективность лечения была максимальной, т. е. найти оптимальные значения элементов матрицы [X_ij], если K₁=60, K₂=40, N₁=30, N₂=20, N₃=50.

Таблица 1.1 – Матрица коэффициентов [C_ij]

		B1	B2	B3
[Cij]=	A1	1	0,3	0,1
	A2	0,2	0,6	1

Таблица 1.2 – Матрица коэффициентов [X_ij]

	x11	x12	x13
[Xij]=
	x12	x22	x23

Метод решения – линейное программирование.

Решение.

1). Проиллюстрируем данную задачу на рис. 1.1.

Рисунок 1.1 – Иллюстрация Задачи 1

2). Для решения задачи запишем уравнения-ограничения (1.1)-(1.5):

3). Выбрем в качестве свободных переменных x₁₁ и x₁₂, тогда базисные переменные будут определяться уравнениями (6)-(9):

4). Функция L с учетом табл. 1 имеет вид уравнения (10):

5). Выражая функцию L через свободные переменные, получаем уравнение (11):

6). Тогда уравнение основной прямой L’=L-14=0 имеет вид уравнения (12):

7). Так как все переменные должны быть неотрицательными, то x₁₃≥0; x₂₁≥0; x₂₂≥0; x₂₃≥0 и из уравнений (6)-(9) получаем неравенства (13)-(16):

Данные условия (вместе с условиями неотрицательности свободных переменных x₁₁≥0; x₁₂≥0) образуют ОДР на рис. 2. На нем же изображена прямая L’=0.

Рисунок 1.2 – Область допустимых решений

Из рисунка видно, что L’ достигает максимума в точке x₁₂=20, x₁₁=30. При этом остальные элементы решения равны:

x₁₃=60-30-20=10

x₂₁=30-30=0

x₂₂=20-20=0

x₂₃=30+20-10=40

L=1,7∙30+0,6∙20+14=77

Таким образом, полученное значение суммарной эффективности равно 77.

Ответ: L=77;

	30	20	10
[Xij]=
	0	0	40

Задача 2.

Больной находится в одном из четырех состояний {S₁, S₂, S₃, S₄}, а у врача есть два варианта лечения: A₁ и A₂. Применение лечения A_i к больному, находящемуся в состоянии S_j, приводит к выздоровлению с вероятностью  a(i,j).

Матрица M_a = [a(i,j)] имеет следующий вид:

Таблица 2.1 – Матрица коэффициентов M_a

	S1	S2	S3	S4
A1	0,6	0,5	0,4	0,3
A2	0,4	0,7	0,8	0,9

Расчетным путем обосновать оптимальное решение врача в данной ситуации:

1) при использовании минимаксной смешанной стратегии для показателя a(i,j) и для показателя полезности f(i,j) = a(i,j) - r(i,j), где r(i,j) - риск , r(i,j) = bj - a(i,j), bj=max{a(i,j)};

2) в случае, когда известны априорные вероятности состояний: P(S₁)=0,8; P(S₂)=0,1; P(S₃)=0,05; P(S₄)=0,05 на основе максимизации среднего значения a(i,j);

3) в случае, когда все состояния равновероятны.

Решение.

I. 1). По матрице определяются нижняя α и верхняя β цены игры. Рассчитанные по этой матрице значения α_i приведены справа от соответствующих строк табл. 2.2, а значения β_j – под соответствующими столбцами.

Таблица 2.2 – Матрица M_a с рассчитанными значениями α_i и β_j

	S1	S2	S3	S4
A1	0,6	0,5	0,4	0,3
A2	0,4	0,7	0,8	0,9

Таким образом, α=0,4; β=0,6. То есть α≠β, из чего следует вывод, что у нас нет устойчивых чистых стратегий, определяемых седловой точкой. Для решения задачи воспользуемся геометрической интерпретацией, представленной на рисунке 2.1.

Рисунок 2.1 – Геометрическая интерпретация игры

Из рисунка 2.1 видно, что нижняя граница выигрыша – прямая BAM, ее максимум достигается в точке A, которая определяет оптимальную стратегию =(p₁, p₂).

Пара оптимальных смешанных стратегий =(p₁, p₂) и =(q₁, q₂). и цена игры определяются по формулам (2.1), (2.2), (2.3), (2.4) и (2.5) соответственно:

Таким образом, γ=0,525; =(0,625, 0,375) и =(0,4375, 0,5625).

(2.6)

2). Матрица рисков M_r получается из M_a на основе соотношения (2.6):

	β1	β2		β3	β4
Mr=						-Ma,
	β1	β2	β3		β4

поэтому M_r имеет вид, представленный в таблице 2.3.

Таблица 2.3 – Матрица рисков M_r

	S1	S2	S3	S4
A1	0	0,2	0,4	0,6
A2	0,2	0	0	0

Матрица M_f сочетанного показателя полезности f_ij определяется разностью M_f=M_a-M_r и имеет вид таблицы 2.4.

Таблица 2.4 – Матрица M_a с рассчитанными значениями α_i и β_j

	S1	S2	S3	S4
A1	0,6	0,3	0	-0,3
A2	0,2	0,7	0,8	0,9

Для этой матрицы также рассчитаны нижняя α*=0,2 и верхняя β*=0,6 цены игры.

Таким образом, α*≠β*, а следовательно, необходимо искать решение в смешанных стратегиях.

Выполним геометрическую интерпретацию игры на рисунке 2.2.

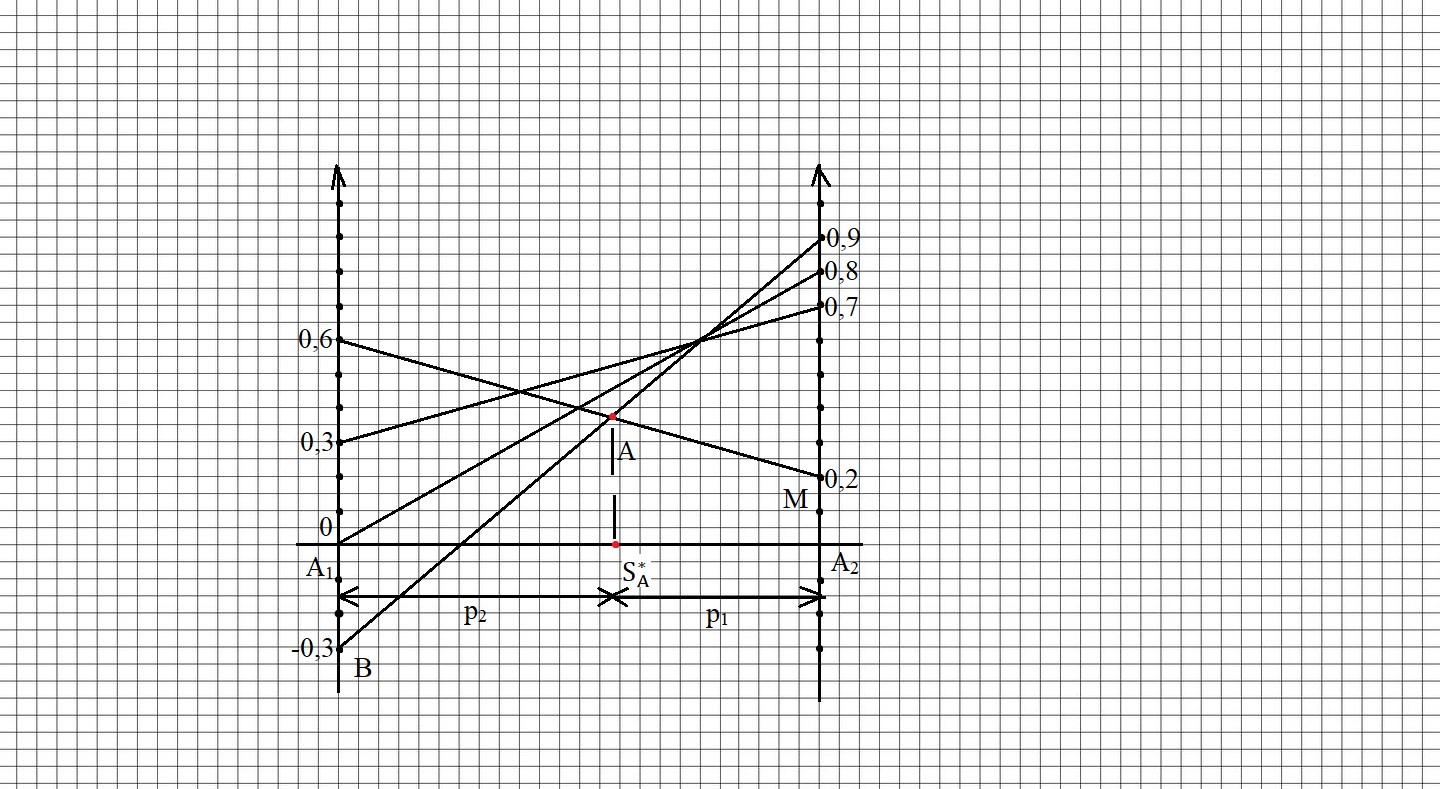
Рисунок 2.2 – Геометрическая интерпретация игры

Из рисунка 2.2 видно, что нижняя граница выигрыша – прямая BAM, ее максимум достигается в точке A, которая определяет оптимальную стратегию =(p₁, p₂).

Пара оптимальных смешанных стратегий =(p₁, p₂) и =(q₁, q₂). и цена игры определяются по формулам (2.1), (2.2), (2.3), (2.4) и (2.5) соответственно:

Таким образом, γ=0,525; =(0,625, 0,375) и =(0,4375, 0,5625).

II. 1). Представим матрицу M_a и априорные вероятности в виде одной таблицы 2.5:

Таблица 2.5 – Матрица коэффициентов M_a и априорные вероятности

	S1	S2	S3	S4
A1	0,6	0,5	0,4	0,3
A2	0,4	0,7	0,8	0,9
Pj	0,8	0,1	0,05	0,05

2). Так как вероятности P_j известны, то при использовании показателя a_ij решение игры находится на основе максимизации среднего значения , где определяется формулой (2.7):

с учетом