
МСИС_КР Архангельский 2154
.pdf
Министерство цифрового развития, Связи и Массовых Коммуникаций Российской Федерации Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное
учреждение высшего образования «Московский Технический Университет Связи и Информатики» (МТУСИ)
Кафедра «Метрологии,стандартизациииизмеренийв инфокоммуникациях»
Контрольная работа
по дисциплине:
«Метрология,стандартизацияиспецификация»
Выполнил: Архангельский М.В.
студент группы БСТ2154
Номер зачетной книжки:
ЗБСТ21001
Проверил:
доцент, Шестаков В.В.
Москва 2025

Задача №1.
Показание цифрового (электронно-счетного) измерителя частоты при измерении периода N=350 мкс.
Найти максимальную абсолютную и относительную погрешности дискретности.
Решение:
Длительность периода измеряемого сигнала N в цифровом (электронносчётном) измерителе частоты определяется при помощи подсчёта количества m эталонных счетных импульсов Т0 прошедших за длительность временного строба Тх, равной (или кратной, что зависит от установленного коэффициента деления) периоду измеряемой частоты.
N=mT0
Погрешность дискретизации определяется тем, что измеряемое значение интервала времени заменяется целым числом периодов следования счётных импульсов. Она возникает вследствие того, что импульс Тх и периодическая последовательность счетных импульсов в общем случае не синхронные сигналы. В реальной схеме измерения непосредственно фиксируется число попавших во временные ворота счетных импульсов, а не число периодов их следования и поэтому, максимальное значение абсолютной погрешности дискретности составляет плюс-минус один период следования счетных импульсов.
Таким образом, максимальное значение абсолютной погрешности дискретности при измерении интервалов времени:
∆д= ± T0,c
Абсолютная погрешность дискретизации не зависит от значения измеряемого интервала времени: она определяется единицей дискретизации, т.е. Т0.

Задача №2.
Измеряется напряжение в виде периодической последовательности прямоугольных импульсов с параметрами= 50 В : длительность импульсов τ=10 мкс, период Т=100 мкс, амплитуда .
Найти чему равно:
1.Показание пикового вольтметра с закрытым входом, проградуированного в среднеквадратических значениях синусоидального сигнала.
2.Показание пикового вольтметра с открытым входом, проградуированного в среднеквадратических значениях синусоидального сигнала.
3.Показание квадратичного вольтметра с закрытым входом, проградуированного в среднеквадратических значениях синусоидального сигнала.
4.Показание вольтметра средневыпрямленных значений с открытым входом, проградуированного в среднеквадратических значениях синусоидального сигнала.
5.Показание вольтметра средневыпрямленных значений с закрытым входом, проградуированного в среднеквадратических значениях синусоидального сигнала.
6.Показание пикового вольтметра с закрытым входом, проградуированного в максимальных значениях синусоидального сигнала.
7.Показание пикового вольтметра с открытым входом, проградуированного в максимальных значениях синусоидального сигнала.
Решение:
Запишем аналитическое описание исследуемого сигнала:
u(t)= U m , 0 ≤ t ≤τ |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
0,τ ≤ t ≤T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Рассчитаем нужные значения напряжения выходного сигнала заданной |
||||||||||||||||||||||||||||||||
формы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пиковое (Um): U m = max{u(t)}=50 В. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
1 |
|
|
( ) |
|
1 |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( −0); |
||||||||||
= |
|
|
|
= |
|
|
|
+ 0 = |
|
|
|
|0 = |
|
|
||||||||||||||||||
Среднее (Uср |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
|
|
050 |
|
|
|
|
|
0 |
−6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
100 10−6 |
(10 10 |
|
|
1 |
− 0) = 5 . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
. |
в |
= |
1 |
|
|
|
|
|
|
|
|
|
|
| | |
= |
|
= |
|
( −0); |
|||||||||||||
|
|
|
| ( )| = |
|
|
|
|
|
|
|0 |
|
|
|
|||||||||||||||||||
Средневыпрямленное (Uср.в): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
. |
в |
= |
|
|
050 |
|
|
|
|
|
|
|
10 |
−6 |
−0) |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
100 10−6 (10 |
|
|
|
= 5 . |
|
|
|
|
|
|
|
|||||||||||||||||||

Среднеквадратическое (U): |
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
2 |
|
1 |
|
|
|
) |
2 |
|
2 |
( −0); |
|
= 0 |
|
( ) = 0 |
|
( |
= |
|
|
||||||
|
502 |
|
10 |
−6 |
|
−0) ≈ 15,81 . |
|
||||||
= 100 10−6 (10 |
|
|
|
||||||||||
Найдем значения напряжения переменной составляющей заданного выходного сигнала, зная, что u ~(t) = u(t) −U cp :
|
|
|
Пиковое (U m ): |
U m = max{u (t)}= max{u(t)−U cp }=50 – 5 = 35 В; |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
~ |
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
в |
Средневыпрямленное значение напряжения переменной составляющей |
|||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
~ |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
(Ucp~ |
.в ): |
|
|
|
| |
|
( )| = |
|
|
|
|
− |
+ |
|
0 − |
|
|
|||||||||||||||||||||||
. |
|
= |
|
|
1 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
= |
|
|
|
|
0 |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
− |0 |
| = |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
= 1 − + |
( |
− ) ; |
|
|
|
|
|
|
|
|
|
|
|
−6 |
|
−6 |
|
|||||||||||||||||||||||
~ в |
= |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
−6 |
+ 5 |
(100 10 |
−10 10 |
) = 9 . |
||||||||||||||||
. |
|
100 10−6 [50 −5] 10):10 |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
Среднеквадратическое (U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
~ = |
1 |
~( ) 2 |
|
= |
1 − 2 + 0 − 2 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
= |
|
1 |
|
|
|
− |
|
|
2 0 |
|
|
+ |
2 |
|
| |
|
|
= |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
0 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= |
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
+ |
|
( − ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
1 |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
~ = |
100 110−6 |
(50 −5)2 10 10−6 + 52 |
(100 10−6 −10 10−6) |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= 15 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Рассчитаем искомые коэффициенты для всего исследуемого сигнала и |
|||||||||||||||||||||||||||||||||||||
его переменной составляющей. |
|
|
|
|
|
|
= |
|
|
= 15 = 1,667 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
= |
15,81 |
= 3,162; |
|
|
|
||||||||||||||||||||||||
|
|
|
Коэффициенты формы (Kф, |
KΦ~ |
): |
|
|
~ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
в |
9 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||
|
= |
|
= |
50 |
= 3,162; |
|
|
|||
|
Коэффициенты амплитуды (Ka, |
Ka~ ): |
|
|
|
|
|
|||
|
|
|
|
15,81 |
|
|
|
|
|
|
|
= |
= 35 = 2,33. |
|
|
|
|||||
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|||
|
|
|
|
|||||||
№ |
Тип преобразователя |
|
|
Уравнение |
преобразования и значение |
|||||
п/п |
вольтметра |
|
|
|
|
показания шкалы |
||||
|
значениях синусоидального |
|
|
|
шк = 0,707 ∙ |
− ср = |
||||
1 |
Показание пикового |
|
|
|
= 0,707 ∙ (50 −5) = 31,815 |
|||||
вольтметра с закрытым |
|
|
|
|||||||
|
сигнала |
|
|
|
||||||
|
входом, проградуированного в |
|
|
|
|
|
|
|
|
|
|
среднеквадратических |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
Показание пикового |
|
|
шк = 0,707 ∙ |
|
= 0,707 ∙ 50 = 35,35 |
||||
значениях синусоидального |
|
|
||||||||
вольтметра с открытым |
|
|
|
|
|
|
|
|
|
|
|
входом, проградуированного в |
|
|
|
|
|
|
|
|
|
|
среднеквадратических |
|
|
|
|
|
|
|
|
|
|
сигнала |
|
|
|
|
|
|
|
|
|
3 |
Показание квадратичного |
|
|
|
|
|
|
= = 15 |
||
|
сигнала |
|
|
|
|
|
||||
|
вольтметра с закрытым |
|
|
|
|
|
шк |
|
|
|
|
входом, проградуированного в |
|
|
|
|
|
||||
|
среднеквадратических |
|
|
|
|
|
|
|||
|
значениях синусоидального |
|
|
|
|
|
|
|||
|
среднеквадратических |
|
|
|
|
шк = 1,11 ср.в = |
||||
4 |
Показание вольтметра |
|
|
|
|
|
|
|
|
|
средневыпрямленных |
|
|
|
|
= 1,11 5 = 5,55 В |
|||||
|
сигнала |
|
|
|
|
|||||
|
значений с открытым |
|
|
|
|
|
|
|
|
|
|
входом, проградуированного в |
|
|
|
|
|
|
|
|
|
|
значениях синусоидального |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
= 1,11 |
= |
||
5 |
Показание вольтметра |
|
|
|
|
|
|
|
|
|
средневыпрямленных |
|
|
|
|
= 1,11 9 = 9,99 В |
|||||
|
сигнала |
|
|
|
|
|||||
|
значений с закрытым |
|
|
|
|
|
шк |
|
ср.в |
|
|
входом, проградуированного в |
|
|
|
|
|
||||
|
среднеквадратических |
|
|
|
|
|
|
|||
|
значениях синусоидального |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
максимальных значениях |
|
|
шк = 1 ∙ − ср = 1 ∙ (50 −5) = |
||||||
6 |
Показание пикового |
|
|
|
|
|
|
= 45 |
|
|
|
вольтметра с закрытым |
|
|
|
|
|
|
|
||
|
входом, проградуированного в |
|
|
|
|
|
|
|||
|
синусоидального сигнала |
|
|
|
|
|
|
|
||

7 |
Показание пикового |
шк = 1 ∙ = 1 ∙ 50 = 50 |
|
вольтметра с открытым |
|
|
синусоидального сигнала |
|
|
входом, проградуированного в |
|
|
максимальных значениях |
|
Если вольтметр проградуирован в значениях параметра,на который реагирует его преобразователь, то показание вольтметра при любой форме измеряемого сигнала равно параметру этого сигнала. В этом случае показания вольтметра не зависят от формы измеряемого напряжения.
Задача №3.
На экране осциллографа Тнаблюдает= 60 мкся периодическая последовательность прямоугольных импульсовр с периодом Т= 20 мкс. Развертка внешняя, длительность развертки .
Нарисовать картинку, которая будет на экране осциллографа при внешней и внутренней синхронизации, считая, что в канале «У» отсутствует линия задержки.
Решение:
Для обеспечения равномерной скорости перемещения электронного луча по оси X генератор развертки электронного осциллографа вырабатывает линейное пилообразное напряжение. Это напряжение должно быть синхронным и синфазным по отношению к входному сигналу, подаваемому на усилитель вертикального отклонения по координате Y.
При совпадении периодов развертывающего напряжения и исследуемого сигнала на экране осциллографа образуется неподвижное для наблюдателя (в действительности многократно повторяющееся) изображение (осциллограмма)
Если период пилообразного напряжения развертки превышает в целое число раз период сигнала, то образуется осциллограмма, отображающая
несколько периодов сигнала. |
|
20 ∙10−6 |
|
|
|||||
|
|
|
|
|
|
||||
При длительности импульсов , следующихмкспериодом , |
|||||||||
при заданном периоде |
развертки |
|
|
2 |
|
= 40на экране, |
осциллографа будет |
||
≤ 2 |
= |
|
р |
60 |
|||||
Для того чтобы |
|
= |
= |
= 3. |
|
||||
наблюдаться целое число импульсовр = 300 мкс |
|
||||||||
|
|
импульсы на экране осциллографа имели устойчивое |
|||||||
изображение должна |
осуществляться синхронизация генератора развертки. В |
||||||||
|
|
|
|
|
|
20 |
|
|
|
осциллографах предусматривается три вида синхронизации – внешняя, внутренняя и от сети.
Синхронизацию от сети применяют для исследования сигналов, частота которых равна или кратна частоте питающей сети (50 Гц).
Наиболеечастоиспользуютвнутреннююсинхронизацию.Вэтомслучае исследуемое напряжение подается на канал "Y", часть исследуемого напряжения подается на генератор развертки G. Исследуемое напряжение как бы“навязывает”свойпериодгенераторуразвертки.При этом линия задержки, включаемая в канал вертикального отклонения осциллографов, задерживает сигнал на время, необходимое для запуска генератора развертки. При отсутствии линии задержки на экране осциллографа не будет виден передний фронт исследуемого сигнала. Линия задержки не должна искажать форму исследуемого сигнала.
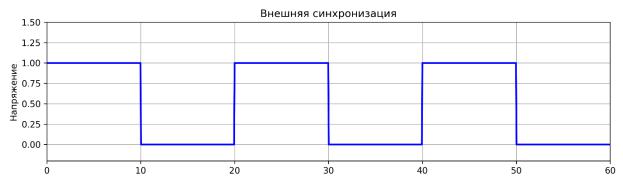
При внешней синхронизации на генератор развертки подается напряжение от внешнего источника сигнала по каналу "X". Синхронизация генератора развертки синхронизируются с внешним сигналом. В этом случае на осциллограф подается два сигнала – исследуемый сигнал и сигнал синхронизации (синхроимпульсы). При этом устойчивое изображение на экране осциллографа (рис. 3.1) получается только тогда, когда эти два напряжения (исследуемое и синхронизирующее развертку) сами будут между собой синхронны.
Получитьполное изображение заданнойпоследовательности импульсов на экране осциллографа:
▪при внутренней синхронизации можно с помощью линии задержки в канале вертикального отклонения;
▪при внешней синхронизации с помощью вспомогательного импульса, опережающим исследуемый импульс и синхронный с ним (линия задержки в канале вертикального отклонения не используется).
При внутренней синхронизации в отсутствие линии задержки между генератором развертки и исследуемым сигналом отсутствует связь по времени. В результате этого сигнал на вертикально отклоняющих пластинах и пилообразное напряжение на горизонтально отклоняющих пластинах будут появляться в разное время. Это приводит к тому, что изображение на экране осциллографа будет смещаться либо вправо, либо влево или вообще происходит срыв изображения (рис. 3.2). При этом ручным регулятором синхронизации можно лишь кратковременно установить изображение.
Рисунок 3.1. Осциллограмма периодической последовательности прямоугольных импульсов с периодом Т = 20 мкс и длительностью развертки Тр = 60 мкс (внешняя синхронизация)

Рисунок 3.2. Осциллограмма периодической последовательности прямоугольных импульсов с периодом Т = 20 мкс и длительностью развертки Тр = 60 мкс (внутренняя синхронизация без линии задержки)
Задача №4.
Цифровым фазометром= 5 кГцизмеряется фазовый сдвиг синусоидальногоТсч = 1 мкс сигнала с частотой . Период счетных импульсов . Определить разрешающую способность (минимальное значение фазы), которое может быть измерено в данном случае.
Решение:
Разрешающая способность цифрового фазометра определяется |
|||||||||
фазометром данного типа и определяется по |
, |
которое |
можно измерить |
||||||
минимальным |
значением сдвига |
фазы |
|||||||
= |
сч |
∙ 360 ° = 5 ∙ 10 |
3 |
∙1 |
∙ 10 |
−6 |
∙360° = |
||
∙ 360 ° = ∙ сч |
|
|
|
||||||
|
|
формуле: |
|
|
|
|
|||
= 1,8°.
Таким образом, минимальное значение фазы определяется заданными значениями частоты измеряемого сигнала и периодом счетных импульсов.

Задача №5. |
|
|
|
|
|
|
При исследовании спектра периодической последовательности |
||||
прямоугольных радиоимпульсов |
длительностью |
|
и периодом |
||
|
|
|
действия с индикатором |
||
Т=20 мкс на анализаторе спектра последовательного с |
= 2 мкс |
|
|||
|
и выразить их в единицах |
|
Та = 400 мкс. |
|
|
на электроннолучевой трубке была получена изображенная ниже картинка. |
|||||
полос1, 2 |
N. |
|
|
Определить значения |
|
Период развертки анализатора спектра |
|
||||
измерения частоты, и число вертикальных
Решение:
Так как по условию исследуется периодическая последовательность
прямоугольных радиоимпульсов, ее спектр является дискретным с частотой |
|||||||||||||||||||||
|
|
0 |
= |
1 |
= |
|
|
|
1 |
|
−6 = 50000 Гц = 50 кГц. |
|
|
||||||||
основной гармоники: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
гармоники: |
|
1 |
|
|
|
|
20 ∙ 10 |
|
собой |
удвоенную |
частоту основной |
||||||||||
Величина |
|
|
представляет |
||||||||||||||||||
Огибающая |
|
|
1 |
= 2 ∙ 0 = 2 ∙50 = 100 кГц. |
последовательности |
||||||||||||||||
|
|
огиб |
|
спектра |
1 |
|
периодической |
||||||||||||||
|
|
= |
1 |
|
= |
|
|
|
= 500000 Гц = 500 кГц. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
прямоугольных радиоимпульсов пересекается с осью абсцисс в точке: |
|||||||||||||||||||||
Число |
|
2 |
|
|
с |
|
|
2 ∙ 10 |
|
|
|
|
|
|
огиб |
|
|||||
|
2 |
= 2 ∙ огиб |
= 2 ∙ |
500 = 1000 кГц = 1 мГц. |
|
: |
|||||||||||||||
Величина |
|
представляет собой−6 |
удвоенную частоту |
|
|
||||||||||||||||
|
вертикальных |
|
полос |
|
|
(спектральных линий) при |
|||||||||||||||
последовательном анализе определяется количеством |
сигналов, прошедших |
||||||||||||||||||||
на вертикально отклоняющие пластины анализатора за время |
а длительности |
||||||||||||||||||||
развертки: |
|
|
|
|
|
= |
а |
= |
400 ∙ 10−6 |
= 20. |
|
|
|||||||||
|
|
|
|
|
|
|
20 ∙10−6 |
|
|
|
|
|
|||||||||
