
Лекция 2
..pdf
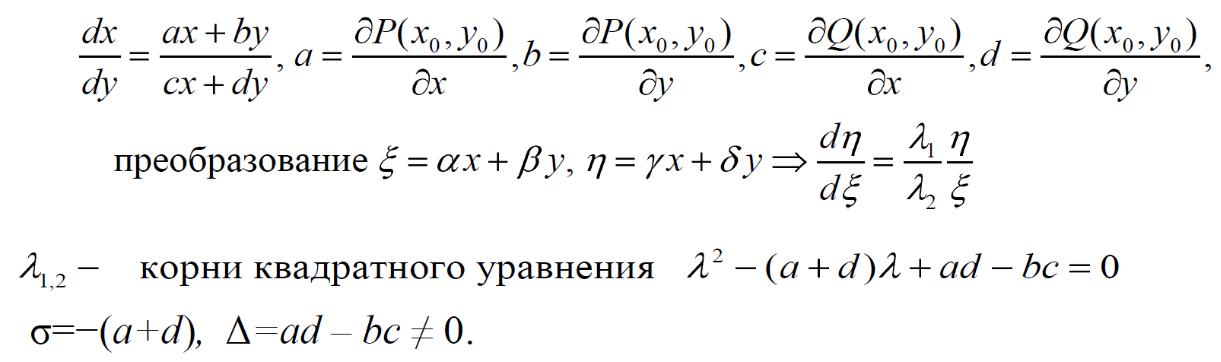
Классификация особых точек Пуанкаре. Поведение фазовых траекторий вблизи
особых точек*
*Степанов В.В. Курс дифференциальных уравнений. – М.: Едиториал УРСС, 2004, стр.78-84.

Случай 1. Корни вещественные и одного знака
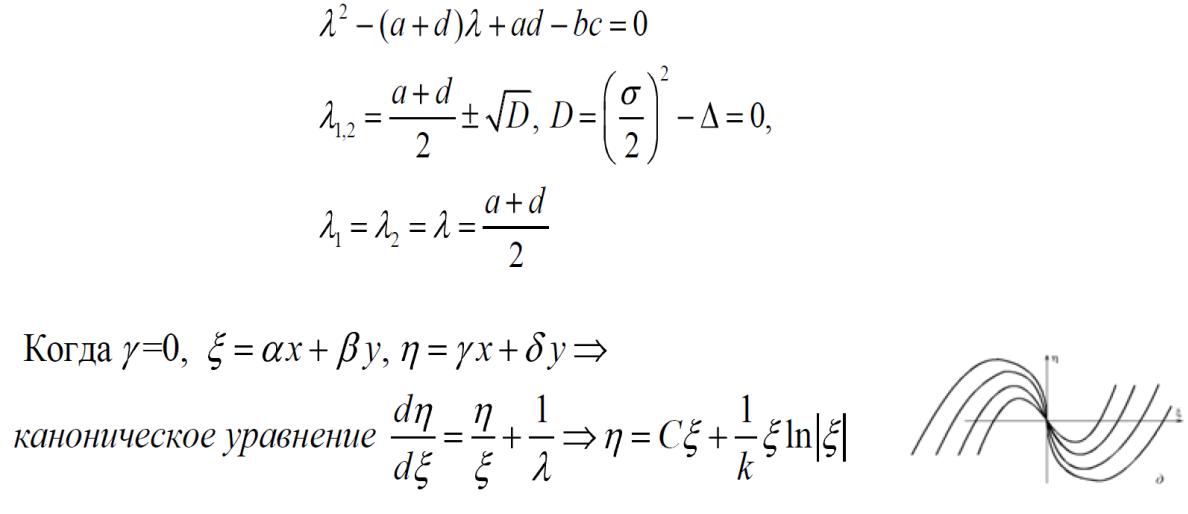
Случай кратных вещественных корней, вырожденный узел:
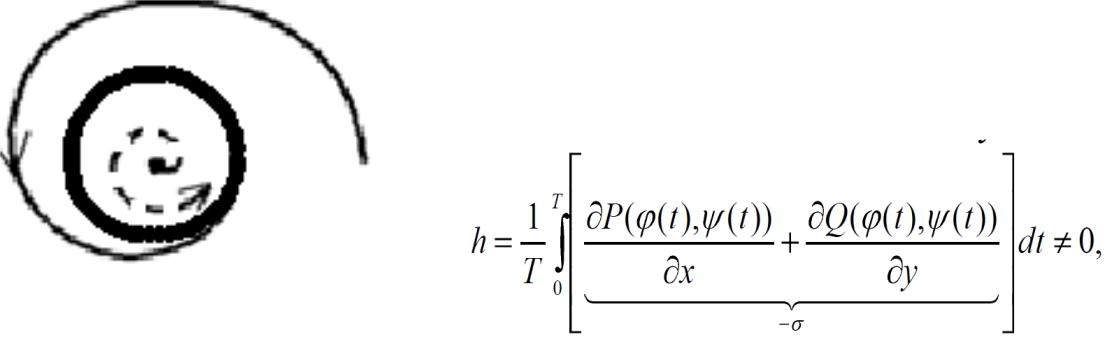
Замкнутые траектории динамической системы и их свойства
Определение 8.
Простым предельным циклом
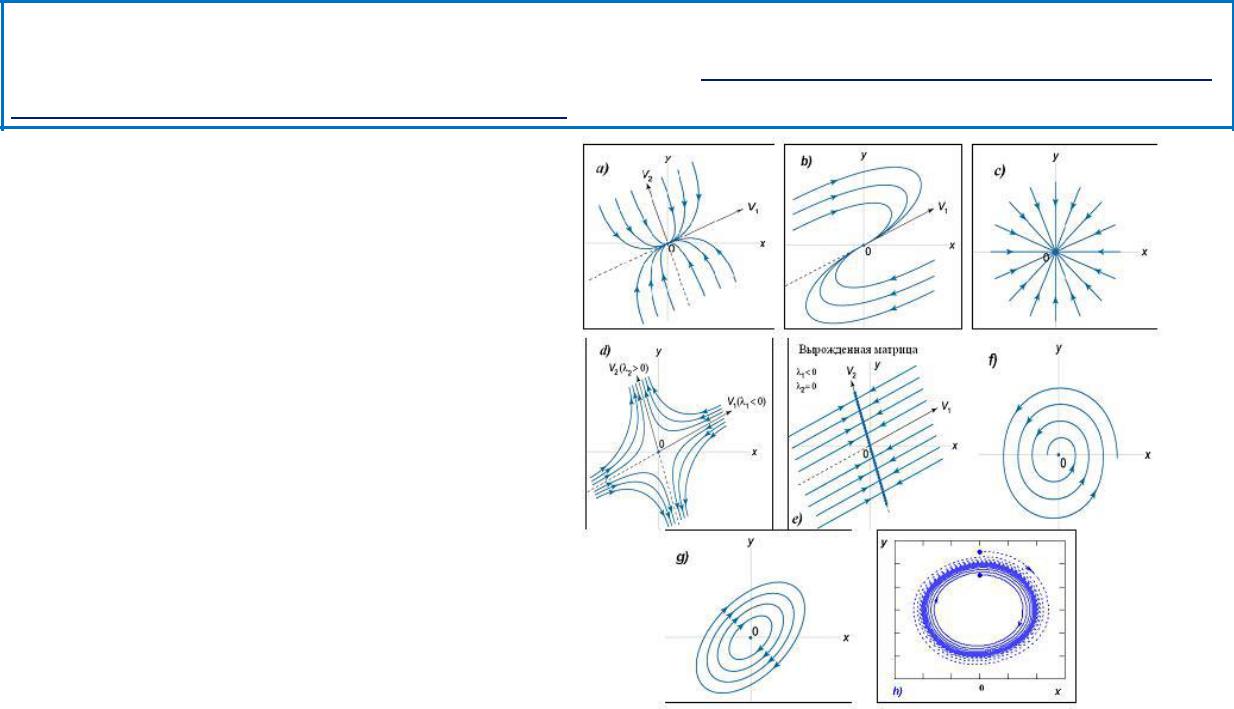
называется замкнутая траектория системы x=φ(t), y=ψ(t), для которой характеристический показатель h отличен от нуля:
Устойчивый предельный цикл.
Траектории, начинающиеся |
|
внутри замкнутого контура и |
где T – период функций φ(t) и ψ(t). |
вне навиваются на него. |
|
Из всех замкнутых траекторий динамической системы грубыми являются лишь простые предельные циклы.
Негрубый предельный цикл исчезает в фазовом пространстве при сколь угодно малых изменениях параметров динамической системы, а грубый – сохраняется даже при изменениях параметров в конечных пределах.
Рис. Типы особых точек и траекторий в системах второго порядка.
Устойчивые: а) узел,
b) вырожденный узел, с) дикритический узел, d) седло,
е) вырожденная матрица А,
f)фокус,
g)центр,
h)предельный цикл.
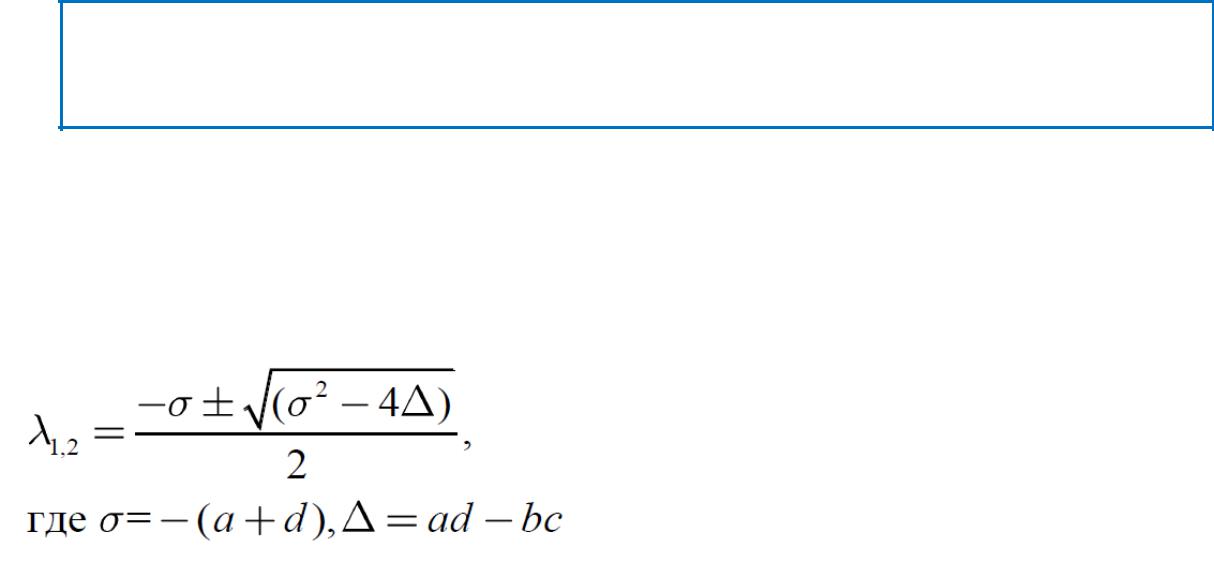
Бифуркации особых точек линейной ДС второго порядка
Определение. Бифуркация – качественная перестройка фазового портрета динамической системы при малых изменениях ее параметров (бифуркационных параметров).
Значения параметров, при которых происходят бифуркации, называются
бифуркационными значениями или точками бифуркации системы.
Бифуркационная диаграмма – изображение смены всех возможных динамических режимов системы при изменении значения бифуркационного параметра.
Если коэффициенты линеаризованной системы (a,b,c,d) зависят от некоторого управляющего параметра, то при изменении этого параметра будут меняться и величины
Δ, σ.
Корни характеристического уравнения линеаризованной системы

Грубым состояниям равновесия на плоскости (σ, Δ) соответствуют все точки плоскости (σ, Δ), кроме точек на оси =0 и на полуоси σ=0, >0.
Точкам на оси Δ=0 и на полуоси σ=0, Δ>0 соответствуют негрубые состояния равновесия. На оси Δ=0 имеем сложные состояния равновесия, detA=0. На полуоси σ=0, >0 возможны состояния равновесия типа центра или центро-фокуса.
При бифуркационных переходах меняется характер устойчивости особой точки. Например, устойчивый фокус через центр может переходить в неустойчивый фокус. Эта бифуркация возможна в нелинейных системах, она называется
бифуркацией Пуанкаре-Андронова-Хопфа. При этой бифуркации в нелинейных системах происходит рождение предельного цикла, и система становится автоколебательной.
В многомерном случае помимо узлов, фокусов, седел, центров и предельных циклов, возможны странные аттракторы, из-за которых многомерные динамические системы могут демонстрировать значительно более сложное поведение.
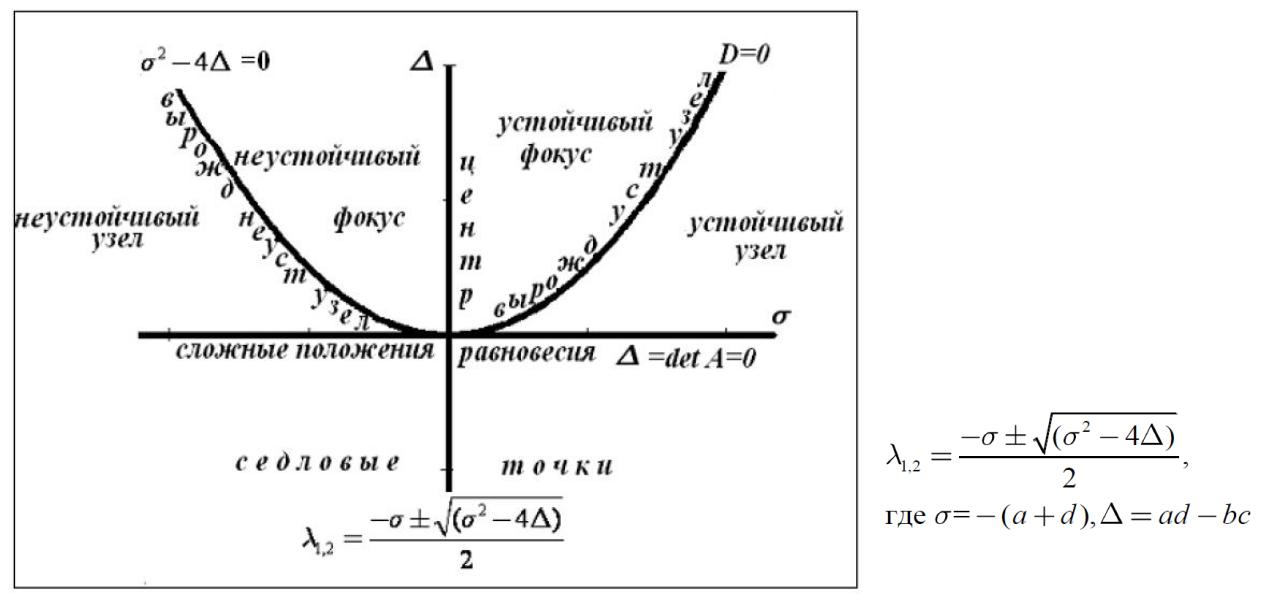
области, которые соответствуют различным типам состояний равновесия в зависимости от корней характеристического уравнения λ1, λ2.
Грубые состояния равновесия и бифуркационная диаграмма на плоскости (σ, Δ)

Обобщающее понятие предельной точки и предельного множества. Аттракторы регулярные и странные. Определения
