
Лекция 2
..pdf
Прикладные задачи нелинейной динамики
Сидоров Станислав Михайлович, Кандидат технических наук, Доцент кафедры прикладной математики
E-mail: xaevec@mail.ru
2024-2025 гг.
ЛЕКЦИЯ 2
Понятие особой точки и особой траектории ДС. Состояние равновесия. Устойчивость по Ляпунову. Исследование нелинейной ДС по первому приближению. Классификация особых точек. Замкнутые траектории. Бифуркации особых точек линейной дифференциальной системы второго порядка. Обобщающее понятие предельного множества. Аттракторы регулярные и странные.
Основой качественного анализа динамических систем является исследование устойчивости.
|
|
|
|
(1) |
|
|
ҧ= (ҧ) |
|
|
|
Пусть |
– область определения функции ( ). |
Предположим, что |
|
0 |
из дифференциальное уравнение (1) имеет решение |
ҧ= φ |
, 0 , |
|
определенное ≥ 0, с н.у. 0 = 0 .
Определение 1. Решение ҧ( ) системы (1) называется устойчивым по Ляпунову, если
> 0 > 0 ≥ 0 0 ҧ0 − 0 < → ҧ − φ , 0 < .
В противном случае решение ҧ( ) называется неустойчивым.
Определение 2. Решение ҧ( ) системы (1) называется асимптотически устойчивым, если оно устойчиво по Ляпунову, и
> 0 |
0 |
ҧ0 |
− 0 |
< → |
lim ҧ |
− φ , 0 |
= 0. |
|
|
|
|
|
→+∞ |
|
|
Любая асимптотически устойчивая фазовая траектория устойчива по Ляпунову. Обратное (в общем случае) не верно.

Устойчивость по Ляпунову |
Асимптотическая устойчивость по |
|
Ляпунову |
Проблема устойчивости и асимптотической устойчивости по Ляпунову связана с анализом реакции системы на малое возмущение ее состояния.
Определение 3. Множество называется инвариантом системы (1), если
0 |
и ≥ 0 → |
φ , 0 |
. |
Простейшим примером инвариантного множества является точка покоя.
Определение 4. Точка ҧ называется точкой покоя системы (1), если
≥ 0 → φ , ҧ ҧ.
Определение 5. Функция ξ( ) является Т-периодическим решением системы (1),
т.е. |
|
|
|
ξ + |
= ξ . |
Множество K = ξ |
| 0 ≤ ≤ |
называется циклом. |
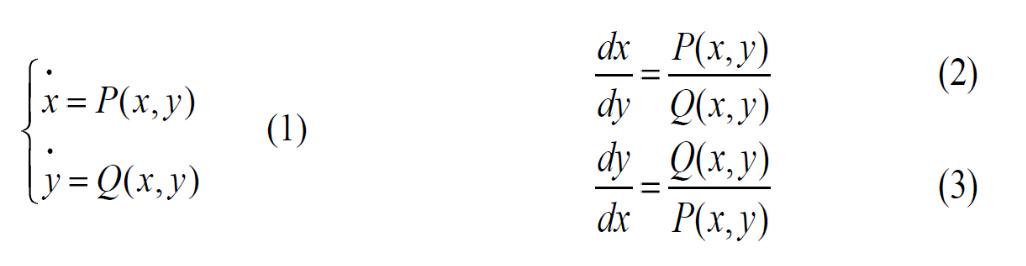
1. Понятие особой точки и особой траектории динамической системы второго порядка
Определение 6. Точка R становится особой точкой в следующих ситуациях: точка R граничная точка области G,
в точке R нарушается единственность решений уравнения (2) или (3),
поле направлений уравнения (2) или (3) в точке R разрывное.
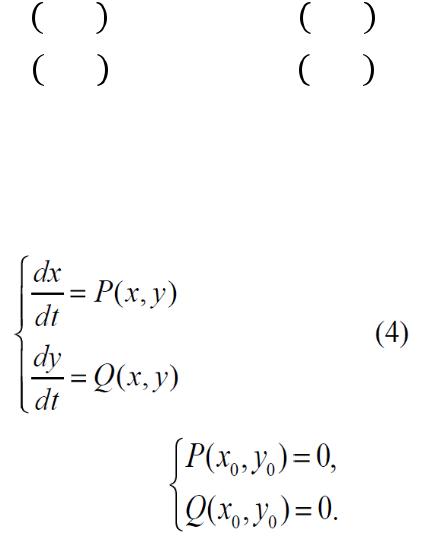
Если существует окрестность точки R такая, что через каждую точку этой окрестности проходит одна и только одна интегральная линия, и хотя бы одна из функций или
, |
или |
, |
|
|
|
||
, |
, |
||
|
непрерывна в этой точке, то R – не особая точка. В противном случае R – особая точка.
Состояниями равновесия R(x0,y0) динамической системы второго порядка
называются общие точки кривых

Система первого приближения (линеаризованная система)


