
Теория графов. Лекция 11
.pdf
Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 11 |
112 |
|
|
Теория графов. Лекция 11
Задача коммивояжёра
Задача коммивояжёра (задача китайского почтальона, Traveler Sales Problem): история появления и исследования задачи коммивояжёра – см. лекцию 1.
11.1. Актуальность задачи коммивояжёра
Задача 1. Шахматный конь. Эта задача решалась ещё Эйлером. Она состоит в нахождении маршрута коня, проходящего через все поля доски по одному разу. Количество замкнутых маршрутов (гамильтоновых циклов) без учёта направления обхода равно 13 267 364 410 532 [5], а с учётом направления обхода – в два раза больше. Задача подсчёта всех возможных незамкнутых маршрутов значительно сложнее и не решена до сих пор. Известно1, что количество незамкнутых маршрутов не превышает числа
сочетаний
C |
63 |
|
|
168 |
|
1.2 10 |
47 |
|
, где 63 – число ходов коня в решении задачи (число
клеток шахматной доски минус одна начальная клетка), а 168 – число допустимых ходов коня без учёта направления на шахматной доске 8 × 8, согласно выражению из [7,8]: n (2 p 3)(2q 3) 1, где n – число ходов
коня на доске размерностью p × q. Один из возможных маршрутов шахматного коня показан на рис.11.1.
Рис. 11.1.
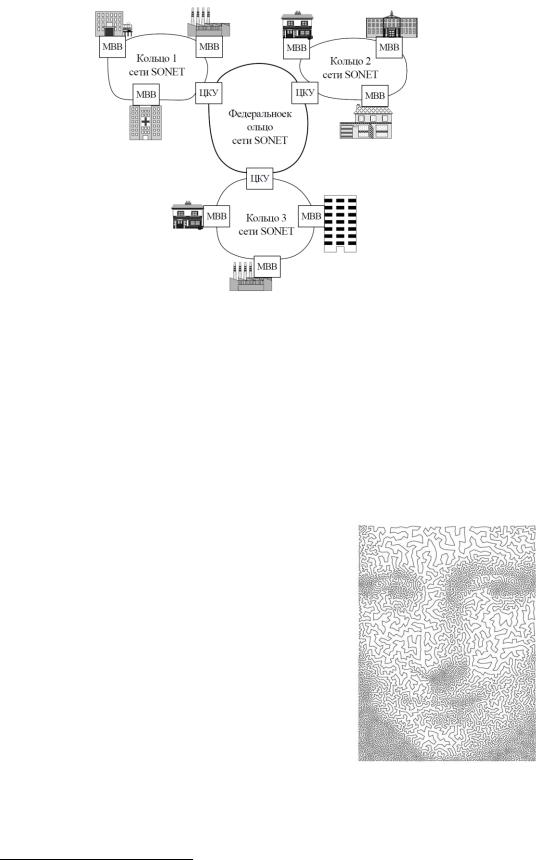
Задача 2. Прокладка кабелей вычислительных сетей. Рассмотрим оптимизационную задачу – прокладку оптоволоконного кабеля по стандарту SDH2 (SONET). При использовании сети SONET узлы соединяются кольцом оптоволокна, каждый из которых передаёт, получает и транслирует сообщения через мультиплексор ввода/вывода. Кольцевые сети объединяются цифровым кроссирующим устройством. Перед телекоммуникационным провайдером стоит задача: соединить клиентов с использованием однонаправленных кольцевых сетей SONET так, чтобы стоимость прокладки сети была минимальной. Каждый узел в сети должен входить только в одно из множества колец. Кроме того, существует ещё
1Гик Е.Я. Шахматы и математика. – М.: Наука, 1983.
2Goldschmidt O., Laugier A., Olinick E.V. SONET/SDH ring assignment with capacity
constraints // Discrete Applied Mathematics, 2003. Vol. 129. P. 99–128.
Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 11 |
113 |
|
|
одно кольцо, называемое федеральным, которое объединяет все кольца. Графически конфигурация сети представлена на рис. 11.2.
Рис. 11.2
При такой конфигурации сети её стоимость складывается из стоимости МВВ, ЦКУ и оптоволоконного кабеля. При фиксированном количестве узлов сети общая стоимость МВВ остается постоянной, поэтому её можно не учитывать, и требуется минимизировать количество ЦКУ и длину оптоволокна.
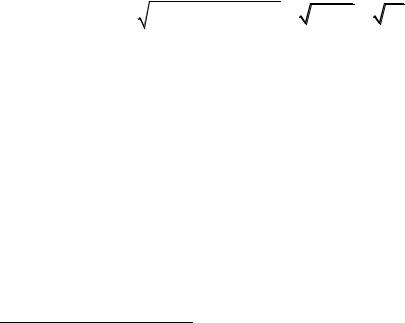
Задача 3. Построение изображений непрерывной линией3. Задача состоит в том, чтобы вычертить одной сплошной черной линией без пересечений чёрно-белое изображение в заданных пределах (рис. 11.3).
Для обработки используются цифровые изображения в оттенках серого. Изображение покрывается множеством точек (вершинами графа), которые размещаются в соответствии с интенсивностью серого цвета. Построение взвешенной диаграммы Вороного (мозаики Вороного, разбиения Дирихле). Для конечного множества точек S (рис. 11.4) она представляет разбиение плоскости, при котором каждую область образует множество точек, более близких к одному из элементов множества S, чем к другому элементу множества (рис. 11.4).
3 Bosch R., Herman A. Continuous Line Drawings via the Traveling Salesman Problem // Operations Research Letters, 2004. Vol. 32. P. 302–303.

Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 11 |
114 |
|
|
Расстояние между точками определяется |
|
интенсивностью серого цвета в этой части |
|
изображения таким образом, что в более тёмных |
|
частях области меньше по размеру, чем в более |
|
светлых, а число таких областей в тёмных |
|
частях больше, чем в светлых. |
Рис. 11.4 |
Если разместить вершины графа в центре каждой области диаграммы Вороного (точки S), получим желаемое покрытие изображения, зависящее от интенсивности серого цвета. Число вершин выбирается так, чтобы получить адекватное описание исходного изображения. Когда выполнено размещение вершин графа, требуется соединить их сплошной линией без пересечений.
В задаче 3 требуется соединить множество точек на плоскости непрерывной линией без пересечений. Это предлагается сделать, решив задачу коммивояжёра (ЗК) в геометрической постановке (эвклидову ЗК), полагая, что все города (точки, вершины) связаны рёбрами, длина каждого из которых равна эвклидову расстоянию между инцидентными вершинами. Одно из свойств оптимального решения эвклидовой ЗК – отсутствие пересечений его фрагментов, а оптимальное решение эвклидовой ЗК – решение задачи построения изображений непрерывной линией.
Что общего между задачами 1-3 и важно в исследованиях задачи коммивояжёра? Основные черты этих задач:
1)легко формализуемы;
2)представимы графом;
3)наличие только детерминированных переменных;
4)один тип объектов (например, таксофоны, АЗС и т.п.) и одно отношение (например, «быть на расстоянии … от …»);
5)высокая вычислительная сложность, простота представления.
Универсальность ЗК объясняется тем, что она представляет класс NP-полных по вычислительной сложности задач в теории алгоритмов.
Класс NP (недетерминированные полиномиальные) включает задачи, которые нельзя решить с помощью детерминированной машины Тьюринга за время, растущее с ростом размерности задачи как полином некоторой фиксированной, не зависящей от размерности задачи, степени.
Термин NP-полная означает, что задача попадает в класс NP, и к ней сводима любая задача из этого класса, т.е. задача является NP-сложной.
Таким образом, к ЗК может быть сведена любая задача из обширного NP класса, что обуславливает интерес к ЗК и актуальность разработки новых методов её решения. Исследования ЗК развиваются в двух направлениях:
1) построение методов решения ЗК, позволяющих ускорить её решение и, соответственно, решать задачи большей размерности (см.
табл. 11.1);

Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 11 |
115 |
|
|
2)приближение ЗК к реальности, добавление объектов и отношений
иразработка методов решения таких задач.
Таблица 11.1
11.2. Постановка задачи коммивояжёра
1. Задача одного коммивояжёра. Пусть имеется n
для каждой пары городов |
i |
и |
j |
задано «расстояние4» c |
|
|
|
|
ij |
городов 1, 2,..., n ;
0 между ними.
Коммивояжёр5 находится в городе 1, он выезжает из этого города, объезжает все города, посетив каждый из них ровно один раз, и возвращается в город 1. Необходимо найти такую последовательность посещения городов, при которой суммарная длина пути минимальна.
Рассмотрим комбинаторную постановку. Введём понятие маршрута.
Под маршрутом будем понимать z = (0, i1, i2, …, in, 0), где i1, i2, …, in – перестановка чисел 1,2,…,n. Длина l(z) маршрута z:
n |
|
|
|
l(z) c |
, |
, |
(i0 in 1 |
k 0 |
ik ik 1 |
|
|
|
|
|
|
0).
|
Пусть Z – |
множество |
всех возможных |
маршрутов, |
Z =n!. |
|||||
|
|
|
|
|
|
c |
|
|
||
4 Заметим, что матрица расстояний |
(c ) |
n n |
может быть как симметричной ( c |
ji |
), так |
|||||
|
|
|
|
ij |
|
ij |
|
|
||
и несимметричной ( cij |
cji ). |
|
|
|
|
|
|
|
||
5 Будем рассматривать задачу одного коммивояжёра. |
|
|
|
|
||||||
Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 11 |
116 |
|
|
Необходимо найти маршрут z0 Z такой, что |
|
l(z0) = min l(z), |
z Z. |
|
|
Это – линейная задача коммивояжёра. |
||||||
|
|
Рассмотрим |
задачу |
на |
узкое |
|||
l1 |
(z) |
max c , |
|
, ( |
, |
) z . Тогда l1(z0) = min l1(z), |
||
|
ik 1 |
ik |
|
ik 1 |
|
|
||
|
|
ik |
|
|
|
|
|
|
|
|
Рассмотрим |
|
постановку |
задачи на |
|||
программирования. Введём булевы переменные:
место. При этом z Z.
языке целочисленного
|
1, |
если коммивояжёр непосредственно |
xij |
|
перезжает из города i в город j, |
|
||
|
|
если нет. |
|
0, |
Тогда суммарная длина маршрута имеет вид:
n |
n |
cij xij min , |
|
i 1 |
j 1 |
условия однократного въезда и выезда из соответственно вид:
n |
|
|
xij |
1, |
j 1, 2,...n , |
i 1 |
|
|
n |
|
|
xij |
1, |
i 1, 2,...n . |
j 1 |
|
|
(11.1)
каждого города имеют
(11.2)
(11.3)
К этим условиям добавляем условия:
|
0 |
|
i 1, 2,...n , |
j 1, 2,...n , |
|
xij |
|
, |
i j . |
||
|
1 |
|
|
|
|
В задаче на узкое место целевая функция имеет вид:
max cij xij min .
xij 1
(11.4)
(11.5)
Если ограничиться указанными условиями (11.2)-(11.4), то получим задачу о назначениях, в оптимальном решении которой может быть несколько циклов.
Нужны специальные условия, которые гарантируют наличие одного цикла. Эти условия имеют вид:
ui |
u j |
nxij n 1, i j, |
(11.6) |
u |
0, |
i 2,..., n, j 2,..., n. |
|
i |
|
|
|
Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 11 |
|
117 |
||
|
|
|
|
|
Получена |
задача |
частично |
целочисленного |
линейного |
программирования.
Рассмотренная задача коммивояжёра называется замкнутой. Можно рассмотреть задачу, в которой возврат в начальный город не предполагается. Такая задача называется открытой. Можно также рассмотреть открытую задачу, у которой начальный и конечный города не фиксированы. Обе эти задачи легко сводятся к стандартной задаче, т. е. к замкнутой задаче, у которой начальный город фиксирован и совпадает с конечным.
2. Задача многих коммивояжёров. Пусть имеется n городов,
множество городов Р=(1,2,…,n). Пусть cij 0 – "расстояние" от города i до города j. Пусть m<<n – число коммивояжёров, каждый из которых находится в одном из городов. Требуется разбить множество из n городов на m непересекающихся подмножеств так, чтобы суммарная длина путей всех коммивояжёров была минимальна.
11.3. Пример решения задачи коммивояжёра в Mathcad®
Рассмотрим пример симметричной задачи коммивояжёра на 6
городов ( n 6 ). (3,5), (3,7), (6,6), (1,1), (4,2), (3,3) – координаты городов.
Коммивояжёр должен выйти из первого города, посетить все города ровно один раз и вернуться в первый город.
Чтобы решать такую задачу, нужно вычислить матрицу расстояний между городами, при этом будем полагать, что её диагональные элементы равны ∞. Например, расстояние между вторым и пятым городами будет равно6:
c |
c |
|
(4 3) |
2 |
(2 7) |
2 |
|
|
|||||
25 |
52 |
|
|
|
|
|
|
1 25 |
26 |
5.1
.
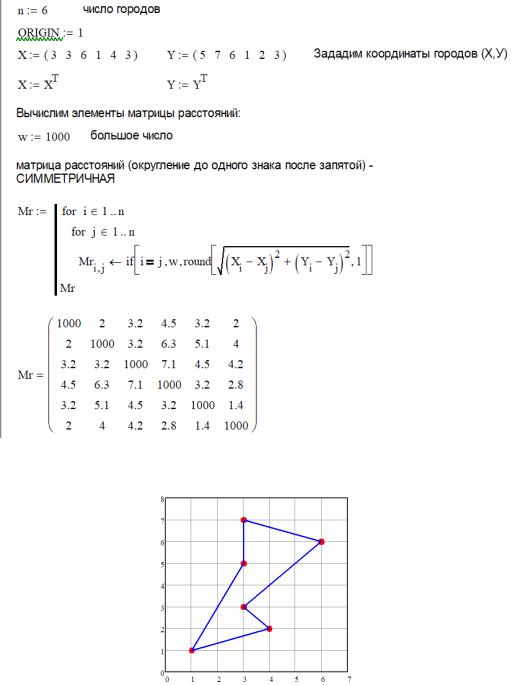
Вычисления выполним в Mathcad® (см. рис. 11.5).
Приближённое решение задачи коммивояжёра можно получить, применяя алгоритм «ближайшего соседа»: из первого города перейдём в ближайший (второй) город, затем из него в ближайший из оставшихся и т.д. При этом нужно следить, чтобы коммивояжёр раньше времени не вернулся в первый город. Получаем маршрут:
1 2 3 6 5 4 1,
его длина равна 2+3.2+4.2+1.4+3.2+4.5=18.5 (см. рис. 11.6).
6 Для упрощения вычислений будем округлять значения cij до одного знака после запятой.
Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 11 |
118 |
|
|
|
|
|
|
|
|
|
|
Рис. 11.5
Рис. 11.6
Выше было сказано, что решение задачи о назначениях совпадает с решением задачи коммивояжёра при наличии одного цикла. Решим задачу о назначениях с матрицей расстояний Mr в Mathcad® (см. рис. 11.7).
Решение задачи о назначениях не является решением задачи коммивояжёра, т.к. получилось два цикла:
1 2 3 1 |
и 4 5 6 1. |
Цена назначения 15.8 даёт нижнюю оценку для оптимального маршрута коммивояжёра.

Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 11 |
119 |
|
|
Рис. 11.7
На рис. 11.8 и 11.9 представлено решение в Mathcad® задачи коммивояжёра методом полного перебора, количество различных маршрутов для n 6 городов равно (n 1)! 5! 120 .
Рис. 11.8

Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 11 |
120 |
|
|
Рис. 11.9
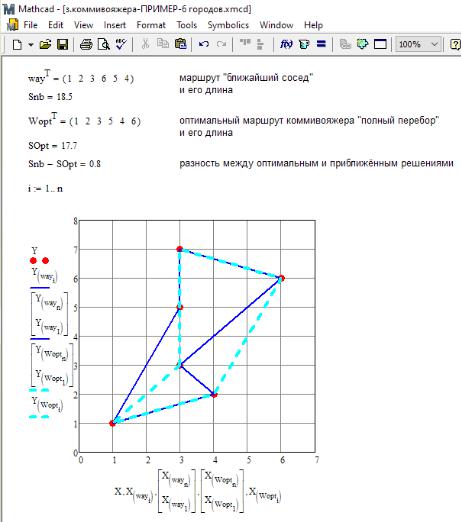
На рис. 11.10 изображены приближённый (сплошная линия) и оптимальный7 (пунктирная линия) маршруты коммивояжёра.
7 Оптимальное решение задачи коммивояжёра можно получить методом ветвей и границ, как это описано в [11], будет рассмотрено в следующей лекции.
Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 11 |
121 |
|
|
Рис. 11.10
11.4. Пример решения задачи коммивояжёра в Excel ®
Рассмотрим решение этой же задачи в Excel®. В п. 11.2 было указано, что нужны специальные условия (11.6), которые гарантируют наличие одного цикла в задаче о назначениях.
Эта задача является задачей частично целочисленного линейного программирования. На рис. 11.11 представлен лист Excel® с исходными данными.
