
Теория графов. Лекция 4
.pdf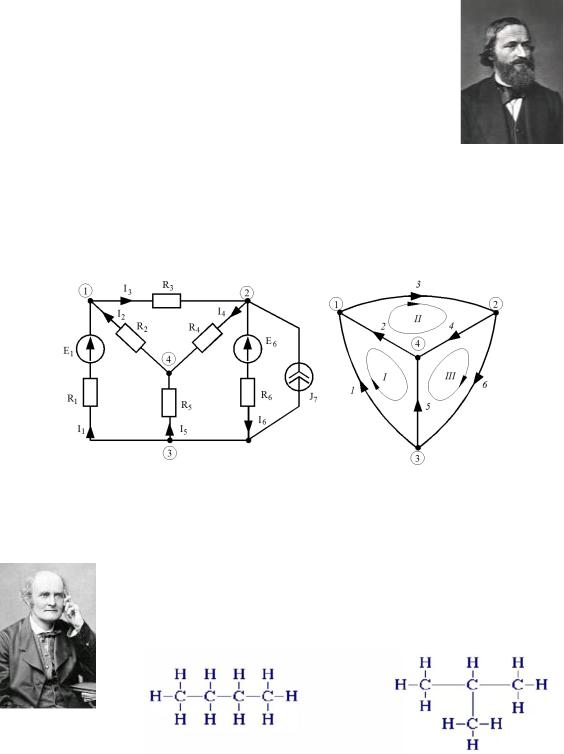
Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 4 |
32 |
|
|
ТЕОРИЯ ГРАФОВ. Лекция 4
4.1. Деревья. История, определения
Рассмотрим особый вид графов, называемый «деревом». Впервые ввёл понятие деревьев физик Густав Роберт Кирхгофф в 1847 году. Будучи студентом Кёнигсбергского университета, он сформулировал законы, управляющие течением тока в электрических сетях. Сети проводов могут быть рассмотрены как графы. Уравнения, которые вытекают из законов Кирхгоффа, не являются независимыми, и Кирхгофф использовал деревья для получения независимого подмножества уравнений (см. рис. 4.1).
Рис. 4.1
Густав Роберт Кирхгофф
(1824-1887)
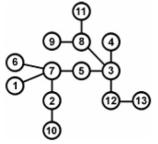
Независимо от Кирхгоффа Артур Кэли, перечисляя изомеры насыщенных углеводородов, еще раз ввёл понятие деревьев и первым исследовал их свойства (см.
рис. 4.2).
Артур Кэли
(1821-1895)
Рис. 4.2

Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 4 |
33 |
|
|
Как чисто математический объект деревья были введены и исследованы Мари Энмон Камилем Жорданом.
Мари Энмон Камиль Жордан
(1838-1922)
Неориентированным деревом называется связный неориентированный граф, не содержащий циклов.
Можно сказать, что дерево является минимальным связным графом в том смысле, что при удалении хотя бы одного ребра он теряет связность.
Несвязный неориентированный граф без циклов, связные компоненты которого есть деревья, называется лесом.
Любая часть леса или дерева также не имеет циклов, то есть является лесом или деревом.
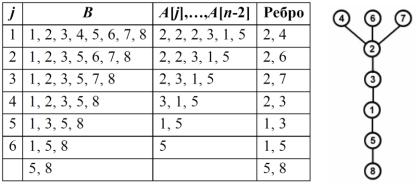
Пример 4.1. На рисунке 4.3 приведены примеры неориентированных деревьев.
Рис. 4.3
Свойства деревьев даёт следующая теорема.
Теорема 4.1. Пусть граф G (V , E) имеет n вершин и m рёбер. Тогда эквивалентными являются такие утверждения:
1)G является деревом;
2)G является ациклическим графом и m = n − 1;
3)G является связным графом и m = n − 1;
4)любые две вершины графа G соединяет единственная простая цепь;
5)G является ациклическим графом, но добавление любого нового ребра способствует возникновению ровно одного цикла.
Следствие 4.1.1. В любом дереве с числом вершин 2 ≥ n имеется не
менее двух концевых вершин.
Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 4 |
34 |
|
|
Следствие 4.1.2. Пусть G − лес с n вершинами и k компонентами, тогда G имеет n − k рёбер.
Часто возникает вопрос, сколько различных деревьев можно построить на n вершинах. Ответ на этот вопрос дает следующая теорема.
Теорема 4.2 (Теорема Кэли). Число различных деревьев, которые
можно построить на n вершинах, равно n |
n 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
||
Пример 4.2. Построить все деревья для графа, имеющего четыре |
|||||||
вершины. |
|
|
|
|
|
|
|
Решение. Для 4-вершинного графа можно построить |
4 |
4 2 |
4 |
2 |
16 |
||
|
|
||||||
деревьев: см. рис. 4.4.
Рис. 4.4
Теорема Кэли имеет много разных интерпретаций и представляет интерес в связи с постановкой задачи о соединении городов: необходимо соединить n городов железными дорогами так, чтобы не строить лишних линий; сколькими способами можно построить такую систему дорог? Практическое значение этой задачи состоит в том, что: если известна стоимость с(A,В) строительства железной дороги между городами A и B, необходимо построить сеть дорог, соединяющих все n городов, имеющую наименьшую возможную стоимость. Теорема Кэли даёт решение этой задачи. Для этого каждому дереву G (V , E) , построенному на n вершинах,
сопоставляется сумма C(G) c( A, B) . Выбрав из этих сумм
( A,B) E
наименьшую, получим решение задачи. Для Кэли, необходимо пересмотреть не больше n
этого, как следует из теоремы
n 2 |
сумм. |
|
Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 4 |
35 |
|
|
4.2. Код Прюфера
Код Прюфера – это способ взаимно однозначного кодирования помеченных деревьев с n вершинами с помощью последовательности n-2 целых чисел в отрезке [1,n]. То есть, можно сказать, что код Прюфера – это биекция между всеми остовными деревьями полного графа и числовыми последовательностями.
Данный способ кодирования деревьев был предложен немецким математиком Хайнцом Прюфером в 1918 году.
Рассмотрим алгоритм построения кода Прюфера для заданного дерева с n вершинами.
Пусть T – дерево с множеством вершин {v1, v2, …, vn}. Будем считать, что номер вершины vi равен i. Сопоставим дереву T вектор (a1, a2, …, an-2) по следующему алгоритму.
1.Найти висячую вершину с минимальным номером i.
2.Записать очередным элементом кода Прюфера номер вершины смежной с i, а вершину i удалить из дерева.
3.Если число вершин дерева больше 2, перейти к шагу 1.
Пример 4.3.
Рис. 4.5
Дерево, изображенное на рисунке 4.5, имеет такой код Прюфера:
(7, 3, 7, 8, 2, 7, 5, 3, 8, 3, 12).
Распаковка кода Прюфера a1, a2, …, an-2 осуществляется по следующему алгоритму (мы допускаем понятные вольности записи).
1.V = {1, 2, …, n} – множество вершин; А = a1, a2, …, an-2 – код Прюфера; i = 0.
2.i = i + 1.
3.Находим в V минимальное число m, не входящее в А; пишем ребро
(m, аi).
4. V = V − m. (удаляем вершину m из списка вершин V)
Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 4 |
36 |
|
|
5. Если i < n − 2, то А = А − аi и возвращаемся к шагу 2; иначе - пишем ребро из двух чисел, оставшихся в V, и завершаем работу. На выходе алгоритма имеем n − 1 рёбер дерева.
Пример 4.4.
Рассмотрим восстановление дерева по коду Прюфера (2, 2, 2, 3, 1, 5). Длина вектора равна 6, следовательно, число вершин в дереве n = 8.
На рис. 4.6 показано результирующее дерево.
Рис. 4.6
4.3. Остовное дерево
Остовным деревом или остовом неориентированного графа G называется остовной подграф, содержащий все вершины графа G и являющийся деревом.
Остовным лесом неориентированного графа G называется остовной подграф, являющийся лесом.
В каждом графе существует остовное дерево. Его можно получить,
применяя алгоритм поиска в ширину:
1. Выбираем произвольную вершину |
v0 |
графа G. Строим дерево T0 |
, |
содержащее одну вершину v0 .
2. Каждой вершине, смежной с вершиной |
v0 |
, присваиваем номер 1. |
Присоединяем к дереву T0 |
вершины с номером 1 и рёбра, инцидентные этим |
вершинам и вершине v0 |
(к каждой вершине с номером 1 присоединяем |
только одно ребро, связывающее её с вершиной v0 ), чтобы сформировать новое дерево T1 .
3. Каждой вершине без номера, смежной с вершинами с номером 1, присваиваем номер 2. Присоединяем к дереву T1 вершины с номером 2 и рёбра, инцидентные этим вершинам и соответствующей вершине с номером 1, чтобы сформировать новое дерево T2 .
Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 4 |
37 |
|
|
4. Повторяем шаг 3 до тех пор, пока не исчерпаем все возможные вершины без номера. Полученное в результате такого построения дерево Tn будет остовным деревом.
Построение последовательности деревьев T0 ,T1,...,Tn при нахождении
остовного дерева алгоритмом поиска в ширину равносильно удалению лишних рёбер в каждом цикле исходного графа.
Число рёбер, которые необходимо удалить в графе G для получения остовного дерева, называется цикломатическим числом графа G и обозначается (G) .
Цикломатическое число является мерой связности графа.
Следствие 4.1.3. Число рёбер произвольного графа G с n вершинами, m рёбрами и k компонентами связности (если граф связный, k =1), которые необходимо удалить для получения остовного дерева, не зависит от последовательности их удаления и равно:
(G) m n k . |
(4.1) |
Следствие 4.1.4. Граф G является лесом тогда и только тогда, когда цикломатическое число (G) 0 .
Следствие 4.1.5. Граф G имеет единственный цикл тогда и только тогда, когда цикломатическое число (G) 1.
Следствие 4.1.6. Граф, в котором число рёбер не меньше, чем число вершин, содержит цикл.
Пример 4.5.
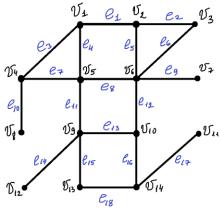
Дан граф, имеющий 14 вершин и 18 рёбер (рис. 4.7). Требуется построить его остовное дерево (остов).
Рис. 4.7
Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 4 |
|
|
38 |
|
|||
Решение. У этого связного (k =1) графа n =14 вершин и m =18 рёбер. |
|||
Применим алгоритм поиска в ширину. |
|
|
|
1. Выбираем произвольную вершину |
v0 v6 (рис. 4.7). Дерево без |
||
рёбер T0 , содержащее одну вершину v0 |
, − |
первое дерево в нашей |
|
последовательности. |
|
|
|
2. Каждой вершине, смежной с вершиной |
v0 |
v6 , присваиваем номер |
|
1 (рис. 4.6, а). Присоединяем к T0 эти вершины и ребра, связывающие их с |
|||
вершиной v0 v6 . В результате получаем дерево |
T1 (сплошные линии на |
||
рисунке 4.8 а)). |
|
|
|
3. Каждой вершине без номера, смежной с вершинами с номером 1, присваиваем номер 2 (рис. 4.8, б). Присоединяем к дереву T1 эти вершины. Добавляем к T1 те рёбра исходного графа, которые соединяют вершину с номером 2 только с одной вершиной с номером 1. В результате получаем дерево T2 (сплошные линии на рис. 4.8, б).
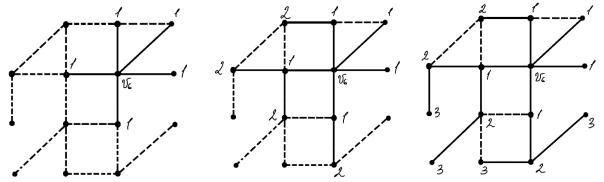
4. Каждой из оставшихся вершин без номера, смежных с вершинами с номерами 2, присваиваем номер 3 (рис. 4.8, в). Присоединяем к дереву T2 эти вершины и добавляем те рёбра исходного графа, которые соединяют вершину с номером 3 только с одной вершиной с номером 2. В результате получаем дерево T3 (сплошные линии на рис. 4.8, в).
а) – дерево
T1
б) – дерево T2 |
в) – дерево T3 |
Рис. 4.8
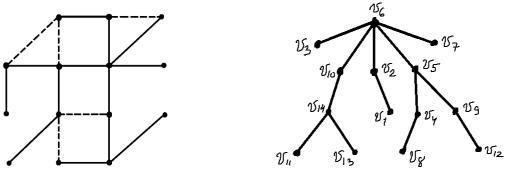
Таким образом, полученное дерево T3 будет являться остовным деревом (рис. 4.9, а).
Надо отметить, что данное дерево является одним из многих остовных деревьев, которые можно получить в исходном графе, выбирая другую
Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 4 |
39 |
|
|
вершину |
v0 |
в качестве начальной и присоединяя к деревьям |
T1 |
другие рёбра.
На рис. 4.9, а) изображён его остов, полученный после(G) m n k 18 14 1 5 рёбер (см. формулу (4.1)).
, |
T2 |
и |
T3 |
удаления
Рис. 4.9, а) |
Рис. 4.9, б) |
На рис. 4.9, б) – тот же остов, но вершины в нём расположены подругому. При таком расположении вершин становится лучше видно, что это дерево.
Цикломатическое число графа равно 5.
В каждом связном графе имеется остовное дерево. В общем случае остовное дерево определено неоднозначно. Возникает вопрос: сколько остовных деревьев имеется в данном графе? Для ответа на этот вопрос необходимо ввести ещё одну матрицу, ассоциированную с графами.
Матрицей Кирхгофа неориентированного графа G с числом вершин n называется квадратная матрица К порядка n с элементами:
где d (vi )
|
1, если вершины vi и v j смежные, |
|
|||
kij |
|
|
и v j |
несмежные, |
(4.2) |
0, если i j и вершины vi |
|||||
|
d (v ), если i j, |
|
|
|
|
|
|
i |
|
|
|
– степень вершины vi , i, j 1,2,..., n .
Теорема 4.3. Число остовных деревьев в связном графе G с числом вершин n 2 равно алгебраическому дополнению любого элемента матрицы Кирхгофа (4.2).

Иванова А.П. ТЕОРИЯ ГРАФОВ. Лекция 4 |
40 |
|
|
Пример 4.6.
Для графа, изображённого на рис. 4.10 записать матрицу Кирхгофа, найти число остовных деревьев.
Рис. 4.10
Решение. Матрица Кирхгофа:
|
1 |
2 |
3 |
4 |
|
|
|
|
|
1 |
3 |
–1 |
–1 |
–1 |
|
|
|
|
|
2 |
–1 |
2 |
–1 |
0 |
|
|
|
|
|
3 |
–1 |
–1 |
3 |
–1 |
|
|
|
|
|
4 |
–1 |
0 |
–1 |
2 |
|
|
|
|
|
Найдём алгебраическое дополнение элемента
k11
:
|
|
1 1 |
|
2 |
1 |
0 |
|
|
3 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||
A |
|
|
1 |
3 |
1 |
|
2 |
( 1) |
0 |
|||||
( 1) |
|
|
|
|
|
|
||||||||
11 |
|
|
|
|
|
|
|
|
1 |
2 |
|
0 |
2 |
|
|
|
|
|
0 |
1 |
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
2(6 1) ( 2 0) 10 2 8. |
|
|
|
|
|
|||||||||
По теореме 4.3 число остовных деревьев равно 8 (см. рис. 4.11).
Рис. 4.11
