
Учебное пособие по начертательной геометрии П.В. Зелёный
.pdf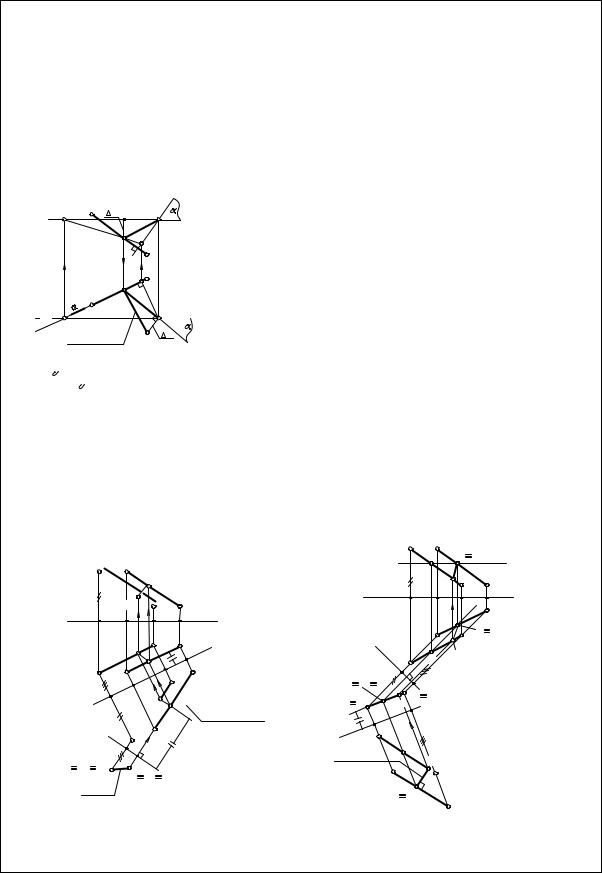

4. Расстояние между скрещивающимися прямыми - определяется |
величиной |
|||||||||||||||||||
перпендикуляра, проведённого от одной из прямых, преобразованной в точку, к |
||||||||||||||||||||
другой прямой (задачи 1 и 2 замены плоскостей проекции). |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
Способ замены плоскостей проекций - задачи 1 и 2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
A" |
|
|
|
D" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K" |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
O" |
B" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
V |
С" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X H |
|
|
|
|
B' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
задача 1 |
|
|
K' |
D' |
V1 |
H1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
B1" |
|
|
B1' |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
С' |
|
|
|
O1' |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
ц |
O1' |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
||
|
|
|
|
|
|
|
|
H |
С1' |
|
|
K1" |
D1" |
1 |
1 |
1 |
|
Н.в. KO (расстояние между |
||
|
|
|
|
|
|
|
|
1 1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
XV |
|
|
|
|
|
C ' |
D ' K ' |
|
скрещивающимися прямыми) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
A1" |
задача 2 |
|
|
|
A1' |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Рис. |
à |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13.11 |
|
|
|
|
|
|
|
|
||
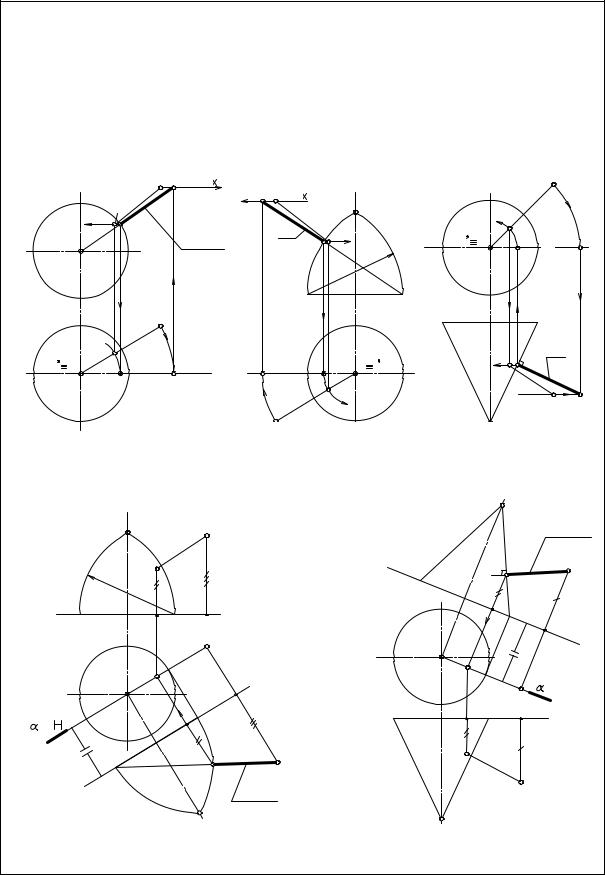
5. Расстояние от точки до плоскости - определяется величиной перпендикуляра, |
||||||||||||||||||||
проведённого из точки на плоскость до точки его пересечения с этой плоскостью. |
||||||||||||||||||||
|
а. Прямой путь (перпендикулярность) |
|
|
|
K" |
|
|
B" |
б. Способ замены плос- |
|||||||||||
|
|
|
|
|
|
|
|
костей проекций |
||||||||||||
|
K" |
|
|
|
" |
|
|
|
|
|
|
|
|
|
|
|
|
(плоскость преобразовать в |
||
|
|
|
п |
|
B" |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
" |
|
|
|
|
|
|
|
A" |
|
|
O" |
h" проецирующую - задача 3) |
|||||
|
|
l " |
л |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
z |
4" |
|
|
|
|
|
|
|
|
|
|
|
z |
|
1" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
XV |
|
|
|
|
|
||||
|
|
|
O" |
|
|
|
h" |
|
|
|
|
|
|
|
С" |
|
|
|
|
|
|
A" |
|
|
|
1" |
|
|
|
|
|
H |
|
|
|
|
X1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
f" 2" |
3" |
С" |
|
Действия: |
|
|
|
|
A' |
|
|
O' |
B' |
|
H V1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
задача 3 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
1. h и f в плоскости |
|
(ABC); |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
1' |
h' |
|
|
|
|||||
|
A' |
|
4' |
|
|
|
2. l |
|
l |
; |
|
|
|
|
|
z |
|
|
||
|
|
|
|
|
B' 3. l |
( h) - (заключить); |
|
|
|
|
|
O1' |
|
|||||||
|
f' |
|
|
|
|
|
K' |
|
|
С' |
|
|
B1' |
|||||||
Нат.вел. 2' |
|
O' |
|
|
|
4. л.п. 3-4 |
> |
(ABC) |
U |
; |
|
|
С1' |
A1' |
|
|||||
|
|
|
|
; |
|
|
|
|
|
|
||||||||||
|
|
3' |
|
|
|
|
5. т. O > (л.п. 3-4)U |
|
|
|
|
|
|
|
Нат.вел. |
|||||
|
|
|
|
|
1' |
6. Нат. вел. KO |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
K0' |
z |
l ' |
|
|
|
h' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
K' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K1' |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 13.12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 13.13 |
|
||||
|
|
á |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
â |
|
|
6. Расстояние между прямой и параллельной ей плоскостью - определяется ве- |
||||||||||||||||||||
личиной перпендикуляра, проведённого из произвольной точки на прямой к плос- |
||||||||||||||||||||
кости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
См. рис. 1313.12.4и, á13, .13â |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 13.4 |
|
|
|
|
|
|
Ëèñò 4 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
211 |
7. Расстояние между параллельными плоскостями - определяется величиной от- |
|||||||||||||||
резка перпендикуляра, опущенного из точки одной плоскости на другую плос- |
|||||||||||||||
кость (до точки пересечения с другой плоскостью). |
|
|
|
|
|
|
|
||||||||
См. рис. 1313,4,.12 иá,13â.13 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
8. Расстояние от точки до поверхности. |
|
|
|
|
|
|
|
|
|||||||
a. Cпособ вращения вокруг проецирующей оси |
|
|
|
|
|
|
|
|
|||||||
|
|
K" |
K0" |
|
|
|
|
|
|
|
|
|
|
K" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
// |
K0" |
K" |
|
|
|
|
|
|
|
|
|
|
|
(M") |
|
|
|
|
// |
S" |
|
|
|
|
|
|
|
|
|
M0" |
|
|
|
н.в. |
M" |
|
|
|
M" |
|
|
K0" |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
O" |
|
Нат.вел. |
|
|
M0" |
R |
|
i |
S' |
M0" |
//H |
|
||
|
|
K' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M' |
|
|
|
|
|
|
|
|
|
M0' |
|
н.в. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
i |
O' |
M0' |
K0' //V |
K0' |
// V |
M0' |
S' i |
|
|
M' |
|
|
K0' |
||
|
|
|
|
|
|
|
M' |
|
|
|
|
|
K' |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
à а. |
|
|
K' |
|
|
á |
б. |
|
S' |
â в. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Рис. 13.14 |
|
|
|
|
|
|
|
||
б. Способ замены плоскостей проекции |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
S1' |
|
|
|
|
|
S" |
|
K" |
|
|
|
|
|
|
|
|
|
Нат.вел. |
|
|
|
(M") |
|
|
|
|
|
|
|
|
|
M1" |
|
K1" |
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H1 |
||
|
|
|
K' |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
S" |
|
|
|
V |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M' |
|
|
|
|
|
|
|
M" |
|
|
|
|
|
|
|
S' |
|
|
|
|
|
|
|
|
|
K" |
h V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
X |
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
K1" |
|
|
|
(M') |
|
|
|
|
|
|
|
H |
|
M1" |
|
|
|
|
|
|
|
K' |
|
|
|
|
X1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
V1 |
|
|
Нат.вел. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
S1" |
|
|
|
|
|
|
S' |
|
|
|
|
|
|
|
ã |
|
|
|
|
|
|
|
ä |
|
|
|
|
|
|
|
|
|
|
|
Рис. 13.5 |
|
|
|
|
|
Ëèñò 5 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
212 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
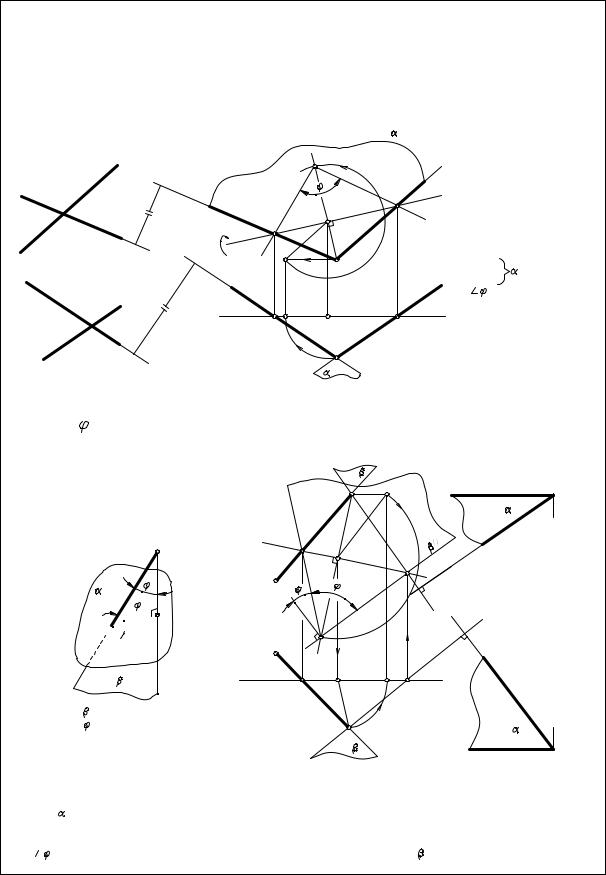

3. Угол |
|
|
между плоскостями |
|
и |
- определяется линейным углом, образо- |
||||||||||||||||||||
ванным двумя прямыми, по которым некоторая плоскость |
, перпендикулярная |
|||||||||||||||||||||||||
плоскостям (или их ребру), пересекает эти плоскости (углом между плоскостя- |
||||||||||||||||||||||||||
ми считают острый угол). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
а. Если на чертеже нет ребра (линии пересечения заданных плоскостей) - угол |
|
определя- |
||||||||||||||||||||||||
ется способом вращения вокруг линии уровня (рис. 13.7,.18)à) |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дано: |
|
|
|
|
|
|
|
|
|
l "( f1") |
|
|
|
|
|
|
|
|
|
|
|
|
l 2"( f2") |
(m // h); |
(аU b). |
|
|
|
|
||||
|
|
|
|
|
|
|
(l |
|
|
l |
|
|
|
|
Требуется: |
|
|
|
|
|
||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
f1" |
|
1 |
2) |
|
|
|
|
- ? |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(а∩? b) |
|
|
|
|
|
|||||
|
(m // h) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
m" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
3" D0" 4" |
i |
|
O" |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
1" |
|
|
|
2" |
|
5" |
h3" |
|
а" (f2") |
1. провести в заданной плоскости |
||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
фронтали и горизонтали; |
|
|
|||||||||
|
h " |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b" (h2") |
|
2. из произвольной точки пространства |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D (D', |
D") провести перпендикуляры l1 и |
||||||||
|
|
|
n" |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
D" |
|
|
|
|
|
|
искомый угол (острый) |
l2 к заданными плоскостям, которые |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определяют плоскость |
(l |
U |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
l2 ); |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
- вращением вокруг горизонтали |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
' |
|
|
|
h3, проведённой в построенной плоско- |
||||||
|
|
|
n' |
|
|
|
|
|
|
|
|
|
|
|
|
|
сти |
(l1 U l2 ). |
|
|
|
|
||||
|
m' |
|
|
|
|
2' |
|
4' |
|
|
|
|
|
|
|
|
l 2'( h2') |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
3' |
|
|
|
|
|
O' |
|
5' |
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f ' |
|
1' |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
b' (h2') |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
h1' |
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
h3' |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
D0' |
x |
D' |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
// |
|
|
|
|
|
а' |
(f2') |
|
l 1 |
|
1 |
|
|
l 2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ребро |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.à13.18 |
|
|
|
|
|
|
|
|
б. Если на чертеже есть ребро (линия пересечения заданных плоскостей) - угол |
|
определя- |
||||||||||||||||||||||||
ется способом замены плоскостей проекций (задачи 1 и 2, рис. 13..7,19)á) |
|
|
|
|
||||||||||||||||||||||
|
|
|
C" |
|
|
D" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
еб |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ребро АВ двугранного угла преобразовать |
|||||||
X V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
A" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
двумя заменами в проецирующую прямую |
|||||||
H |
|
|
|
|
D' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
X2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
A' |
|
|
|
|
|
|
|
|
|
H1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
C' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
ребро |
|
B1" |
|
|
|
A1' |
B1' |
' |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
X1 |
H |
A1" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D1' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D1" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
задача 1 |
|
|
|
|
C1" |
|
|
|
|
|
|
|
С1' |
|
задача 2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
á |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 13.7 |
|
|
|
|
|
|
Ëèñò 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
214 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перечень вопросов, выносимых на экзамен по начертательной геометрии
1.Метод проекций. Центральные и параллельные проекции. Свойства параллельных проекций. Косоугольные и прямоугольные (ортогональные) проекции.
2.Метод Г. Монжа. Четверти и октанты пространства. Образование проекционного комплексного чертежа.
3.Точка в системе трех плоскостей проекций Н, V и W. Проекции точки в системе прямоугольных координат. Европейская и американская системы расположения изображений на чертежах.
4.Прямая линия. Прямые общего и частичного положений относительно плоскостей проекций. Характерные признаки этих прямых на чертеже. Теорема о принадлежности точки прямой.
5.Деления отрезка прямой на чертеже в заданном отношении (свойство параллельных проекций). Построение на чертеже натуральной величины отрезка прямой общего положения и углов его наклона к плоскостям проекций Н и V способом прямоугольного треугольника. Построение на прямой проекций отрезка заданной величины.
6.Следы прямой. Построение на чертеже проекций фронтального и горизонтального следов прямой общего положения.
7.Взаимное положение прямых. Прямые параллельные, пересекающиеся и скрещивающиеся. Характерные признаки на чертеже параллельных, пересекающихся и скрещивающихся прямых. Конкурирующие точки на скрещивающихся прямых.
8.О проекциях плоских углов. Теорема о проецировании прямого угла (прямая и обратная). Привести наглядный рисунок с доказательствами (согласно прямой и обратной теоремам о трех перпендикулярах). Теорема
оделении пополам проекций острого или тупого углов.
9.Плоскость. Способы задания плоскости на чертеже. Следы плоскости. Теоремы о принадлежности прямой и точки плоскости. Прямые особого положения в плоскости (фронталь, горизонталь, линия наибольшего ската) и их построение на чертеже.
10.Характерные положения плоскости относительно плоскостей проекций. Плоскости общего и плоскости частных положений. Характерные признаки этих плоскостей на чертеже. Проведение через прямую общего положения проецирующей плоскости (заключение прямой в плоскость) и обозначение этого действия на чертеже.
11.Взаимное положение прямой и плоскости, двух плоскостей. Признаки параллельности прямой и плоскости, двух плоскостей. Построение на чертеже плоскости, параллельной заданной.
12.Пересечение прямой и плоскости, двух плоскостей. Частные случаи пересечения и общий случай пересечения. Графический алгоритм построения точки пересечения прямой общего положения с плоскостью общего положения. Построение линии пересечения плоскостей общего положения по точ-
215
кам пересечения прямых общего положения с плоскостью общего положения (случай, когда проекции плоскостей на чертеже накладываются).
13.Перпендикулярность (частный случай взаимного положения прямой и плоскости двух плоскостей). Теоремы о перпендикулярности прямой
иплоскости, двух плоскостей. Теорема о проецировании прямого угла. Проведение на чертеже проекций перпендикуляра к плоскости и плоскости, перпендикулярной к заданной прямой.
14.Задачи трех типов о перпендикулярности прямой и плоскости и характерные графические действия для каждого типа задач:
а) провести проекции перпендикуляра из точки на плоскости в пространство; требуется построить на проекциях перпендикуляра проекции отрезка заданной величины;
б) провести проекции перпендикуляра из точки в пространстве к плоскости; требуется построить проекции точки пересечения перпендикуляра с плоскостью;
в) построить плоскость, перпендикулярную к заданной прямой (требуется построить точку пересечения построенной плоскости с заданной или другой прямой).
15.Преобразование чертежа. Способы преобразования и их сущность:
способ замены плоскостей проекций; четыре задачи преобразования прямой и плоскости этим способом;
способ вращения вокруг проецирующей прямой;
плоскопараллельное перемещение (частный случай способа вращения вокруг проецирующей прямой);
способ вращения вокруг прямой уровня (фронтали или горизонтали).
16.Определение угла между прямой и плоскостью и между двумя плоскостями.
17.Поверхности. Способ образования поверхностей (кинематический). Образующая и направляющая линии, каркас поверхности, определитель поверхности; очерк поверхности на чертеже; каркас поверхности.
18.Гранные поверхности. Образование. Геометрические тела – призма и пирамида. Построение проекций точек на поверхности, построение сечений плоскостями частного положения.
19.Кривые линии. Плоские и пространственные кривые линии. Винтовые линии. Построение пространственной конической и цилиндрической винтовых линий. Характеристики винтовых пространственных линий.
20.Кривые линейчатые поверхности (с прямолинейной образующей). Цилиндрическая и коническая поверхности. Эллиптические поверхности. Линейчатые поверхности вращения. Образование. Порядок поверхности. Геометрические тела – круговой цилиндр и круговой конус. Построение проекций точек на поверхностях цилиндра и конуса. Сечение поверхностей цилиндра и конуса плоскостями частного положения.
21.Нелинейчатые поверхности вращения (с криволинейной образующей). Образование. Порядок поверхностей. Характерные линии на поверх-
216
ности вращения. Геометрические тела – шар и тор (открытый, замкнутый, самопересекающийся – тороид и глобоид). Сечения поверхностей шара и тора (кривые Персея) плоскостями частного положения.
22.Прочие линейчатые и нелинейчатые поверхности вращения – эллипсоид (сжатый и вытянутый), параболоид, одно- и двуполостный гиперболоид. Образование. Показать образования однополостного гиперболоида вращением отрезка прямой линии вокруг оси (отрезок и ось – скрещивающиеся прямые).
23.Некоторые кривые поверхности. Поверхности с одной прямолинейной направляющей – цилиндрические, конические и торсы. Поверхности
сдвумя прямолинейными направляющими и плоскостью параллелизма – коноид, цилиндроид, косая плоскость. Поверхности с тремя прямолинейными скрещивающимися направляющими – однополосный гиперболоид.
24.Кривые нелинейчатые поверхности (не вращения). Поверхности циклические. Поверхности, задаваемые каркасом (графические и топографические поверхности).
25.Винтовые линейчатые поверхности. Образование. Прямой и косой геликоиды. Построение проекций точек на поверхности геликоида. Сечение поверхностигеликоидаплоскостью, перпендикулярнойоси(спиральАрхимеда).
26.Касательные плоскости. Задание на чертеже. Проведение касательных плоскостей к поверхностям цилиндра, конуса, шара и тора в заданной точке поверхности. Нормаль к поверхности.
27.Пересечение поверхностей геометрических тел с прямой линией. Графический алгоритм построения проекций точек пересечения прямой
споверхностью. Пересечение поверхностей геометрических тел плоскостью общего положения. Графический алгоритм построения линии пересечения плоскости общего положения с поверхностью.
28.Пересечение двух поверхностей. Понятие о линии пересечения. Частные случаи пересечения поверхностей геометрических тел:
боковые поверхности двух тел занимают проецирующее положение относительно плоскости проекций (призма и цилиндр);
боковая поверхность одного тела занимает проецирующее положение относительно плоскости проекций;
пересечение поверхностей геометрических тел вращения (кроме открытого тора), расположенных соосно (поверхности имеют общую ось вращения);
пересечение поверхностей геометрических тел вращения второго порядка, имеющих двойное соприкосновение и описанных вокруг сферы (построение проекций линии пересечения по теореме Г. Монжа).
29.Пересечение поверхностей. Общие случаи пересечения. Способы посредников. Сущность способа посредников. Графический алгоритм построения проекций линии пересечения поверхностей способом посредников.
Рассмотренные способы посредников:
способ вспомогательных секущих плоскостей;
217
способ вспомогательных концентрических сфер;
способ вспомогательных эксцентрических сфер.
30.Пересечение поверхностей многогранников. Графический алгоритм построения пространственной ломаной линии пересечения гранных поверхностей.
31.Развертывание поверхностей. Поверхности развертываемые и неразвертываемые. Понятие развертки поверхности. Точные и приближенные развертки.
32.Развертка боковой поверхности призмы:
способом триангуляции (способом треугольников);
способом нормального сечения;
способом раскатки.
Условия применения каждого способа.
33.Развертка боковой поверхности пирамиды способом треугольников.
34.Развертка цилиндра:
способом нормально сечения;
способом раскатки.
Аппроксимация (замена) цилиндрической поверхности призматической для построения приближенной развертки.
35.Развертывание поверхности кругового конуса. Формула угла развертки. Приближенная развертка аппроксимацией (заменой) конической поверхности пирамидальной.
36.Приближенные развертки сферической и торовой поверхностей.
37.Аксонометрические поверхности. Определение. Прямоугольные и косоугольные проекции. Коэффициенты искажения по аксонометрическим осям и приведенные коэффициенты искажения. Изометрические, диметрические и триметрические проекции. Теорема К. Польке – Г. Шварца «Основное предложение аксонометрии».
38.Стандартные аксонометрии по ГОСТ 2.317–2011.
39.Прямоугольная изометрия. Расположение аксонометрических осей, расположение больших и малых осей и величины эллипсов, коэффициенты искажения. Привести способ построения эллипсов (четырехцентровых овалов) в прямоугольной изометрии.
40.Прямоугольная диметрия. Расположение аксонометрических осей, расположение и величины больших и малых осей эллипсов, коэффициенты искажения. Привести способ построения эллипсов (четырехцентровых овалов) в прямоугольной диметрии.
41.Косоугольная диметрия. Расположение аксонометрических осей, расположение и величины больших и малых осей эллипсов, коэффициенты искажения. Привести способ построения эллипсов (четырехцентровых овалов) в косоугольной диметрии.
На рис. 13.8 приведен образец оформления графической части ответов на экзаменационный билет (допускаетсяих размещениеи сдвух сторон листа).
218

1. Построить три проекции сложного геометрического |
2. Построить проекции пирамиды SABC |
высотой 35мм |
|||||||||||||||||||||||
|
|
тела с линиями пересечения поверхностей. |
|
|
с основанием АВС. Основание высоты O лежит в центре |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
H |
B'' |
S'' |
|
îêружности, описанной вокруг |
ÀÂÑ |
|||||||||
|
|
|
|
|
|
|
|
|
|
l'' |
|
|
|
|
|
|
|
|
|
(SO |
ÀÂÑ) |
||||
|
|
|
|
D'' |
|
|
D''' |
|
|
2'' |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
h'' |
|
|
O'' |
|
|
ZS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1'' |
|
1''' |
|
A'' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
1'' |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2'' |
|
|
2''' |
|
V |
|
|
|
C'' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
A'1 |
||||
|
|
|
|
|
|
|
|
3''' |
H |
|
|
S' |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
3'' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C'1 |
|
|
|
|
||||
|
|
|
|
|
4'' |
|
|
4''' |
|
h' |
|
|
|
|
|
|
|
ZS |
|
O'1 S'1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l'1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
5'' |
|
|
5''' |
|
A' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C'C'' |
|
|
|
|
|
|
|
|
|
2'1 |
|||
|
|
|
|
|
|
|
Å''' |
|
|
l' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Å'' |
|
|
6'' |
|
|
6''' |
|
|
2' |
O' |
|
1' |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
7'' |
|
|
|
7''' |
|
|
|
|
|
|
|
|
|
S'' |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
F'' |
G'' |
|
|
|
|
|
|
|
|
|
|
|
A'' |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
A''' |
|
B'' C'' |
B''' |
A''' F''' |
C''' |
|
|
B' |
|
|
1 |
|
|
|
|
|
|
|
|
B'1 |
|
|||
|
|
|
|
|
|
|
O'' |
|
|
|
ì |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
ì |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
2'' |
|
|
|
|
|
|
|
H1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
1 |
|
|
|
|
|
|
V1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V1 |
|
|
|
B'' |
|
X2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Построить проекции точки О(О,О''-?) на |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
поверхности коноида, цилиндроида и |
косой плоскости |
1" |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
A" l" |
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
1'' |
|
m'' |
3'' |
|
m" |
l" |
|
|
n" |
C" |
|
2" |
|||
|
Å |
|
|
D |
|
|
|
|
|
2'' |
O'' |
|
|
|
|
|
|
|
3" |
||||||
|
|
|
|
|
|
|
3'' |
|
|
|
|
|
|
|
|
|
|
|
|||||||
A |
|
|
|
|
|
|
|
|
|
|
|
2'' |
|
O" |
|
|
|
|
|
|
|
O" |
|
|
|
|
|
|
|
1 |
|
|
|
l'' |
|
|
|
1" |
|
|
|
|
|
|
|
|
|
D" |
|||
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B" |
|
||||
|
F |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
A |
|
|
B O |
|
D |
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
O |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
4 |
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
l |
|
|
|
3 |
|
|
|
|
G |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||
|
|
|
6 |
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
O |
3 |
m |
|
|
|
|
|
|
C |
1 |
O''-? |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
C |
|
Семейство |
|
1 |
|
|
|
|
|
l |
|
|
|
n |
|
Вспомогательные |
||||
|
|
|
|
|
|
|
|
O''-? |
|
O''-? |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
линии |
|
|||||||||
|
|
|
|
|
|
|
образующих |
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H , |
V è V - плоскости |
|
|
ÁÍÒÓ |
Экзаменационная работа |
|
||||||||||||
|
|
|
|
|
|
|
|
параллелизма |
|
|
Разработал |
|
|
|
|
|
|
|
|
Билет ¹ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Проверил |
|
|
|
|
|
|
|
|
|
Ãð. |
|
|
219 |
|
|
|
|
|
|
|
Рис. 13.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 (h
(h  (h
(h  K'
K'
 - ?
- ?
 (h
(h 
 - ?
- ?

