
Учебное пособие по начертательной геометрии П.В. Зелёный
.pdf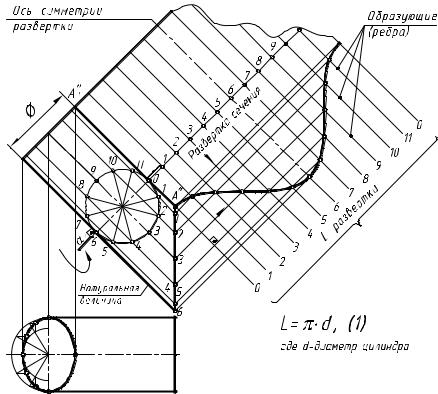
которым заменяется окружность сечения, и провести направления ребер (образующих), перпендикулярно линии сечения (линии пронумеровать), то есть выполнить от ребра А"-А1" последовательную раскатку граней призмы, заменившей цилиндр.
3-е действие. Построить конечные точки каждой образующей (ребра) на пересечении образующих с линиями, проведенными перпендикулярно образующим из одноименных точек нижнего основания.
4-е действие. Оформить чертеж развертки боковой поверхности цилиндра, соединив построенные конечные точки образующих плавными кривыми линиями (в примере развертка оборвана из-за недостатка места).
Для построения более точной развертки следует по формуле (1) (рис. 9.5, где L – диаметр цилиндра) вычислить длину развертки и разделив эту длину на 12 равных частей, провести образующие и далее выполнить 3 и 4 действия алгоритма.
Рис. 9.5
Р а з в е р т к а к р у г о в о г о к о н у с а На рис. 9.6 показан пример построения развертки боковой поверхно-
сти прямого кругового конуса со срезом фронтально-проецирующей плоскостью α(αV), которая пересекает его поверхность по эллипсу.
Построение развертки боковой поверхности конуса выполняется по алгоритму, приведенному выше для построения развертки пирамиды, с некоторыми дополнениями.
Развертка выполняется по предлагаемому алгоритму.
1-е действие. Заменить прямой круговой конус вписанной правильной 12-угольной пирамидой с ребрами-образующими.
150

2-е действие. Построить развертку боковой поверхности пирамиды по натуральным величинам ребер (образующих) и сторон основания, выполнив следующие графические действия:
2.1.Отметить на свободном поле чертежа точку S и провести дугу радиусом L, равным натуральной величине всех образующих конуса (ребер пирамиды).
2.2.Отметить на дуге точку O на вертикальной линии симметрии развертки и построить вправо и влево на дуге засечками, равными сторонамхордам 12-угольника, точки, соответствующие вершинам этого многоугольника; пронумеровать эти точки и соединить их с вершиной развертки, построив таким образом вспомогательные ребра-образующие (грани пирамиды).
3-е действие. Достроить на развертке линию среза конуса фронталь-
но-проецирующей плоскостью α(αV), выполнив следующие графические действия:
3.1.На фронтальной проекции конуса перенести горизонтально на натуральную величину образующей S"-6" точки сечения, отмеченные на вспомогательных образующих, то есть вращением вокруг оси i(i",i') построить натуральные величины отрезков образующих-ребер сечения.
3.2.Отложить на соответствующих образующих развертки натуральные величины отрезков образующих-ребер до точек сечения (отмечены на
фронтальной проекции и на развертке фигурными скобками отрезки O"-Oo" образующей для точки Oо и 2"-2о" образующей для точки 2o) и соединить построенные точки сечения на развертке плавной кривой линией.
4-е действие. Оформить чертеж развертки, проведя сплошными толстыми линиями контур построенной развертки.
Рис. 9.6
151

Для построения более точной развертки следует вычислить по форму- |
|||||||||||||||||||||||||
ле (2) (рис. 9.6, где R – радиус основания конуса; L – длина образующей |
|||||||||||||||||||||||||
конуса) угол развертки и разделить дугу развертки на 12 равных частей, |
|||||||||||||||||||||||||
провести образующие и далее выполнить 3 и 4 действия алгоритма. |
|
|
|
||||||||||||||||||||||
На рис. 9.7, а дан чертеж поверхностей кругового цилиндра и кругового |
|||||||||||||||||||||||||
конуса, описанных вокруг сферы, и построена линия пересечения этих по- |
|||||||||||||||||||||||||
верхностей по теореме Г. Монжа. На рис. 9.7, б построена развертка кони- |
|||||||||||||||||||||||||
ческой части этой конструкции по следующему графическому алгоритму: |
|
||||||||||||||||||||||||
1-е действие. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Провести |
произ- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ц |
|
|
|
|
|
|
|
|
|
вольное |
сечение, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
перпендикулярное |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3о |
2о |
|
1о |
0i |
||
оси конуса, и повер- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
ik" |
|
|
|
|
|
|
4о |
|
|
|
|
|||
нуть половину ок- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5о |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
2" K" |
1" |
0" |
|
|
|
|
|
|
||||
ружности |
сечения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
3" |
|
|
|
6о |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
в очерковую плос- |
6" |
|
|
5" |
|
|
|
4" |
|
|
|
|
|
|
|
|
3 |
2 |
1 |
0о |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
кость конуса. |
5О" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
хорда |
|
|
симметрии |
||
2-е |
действие. |
4О" |
|
|
|
|
|
|
|
|
|
|
|
|
|
1о |
0о |
|
5 |
|
|
|
|||
|
3О"О |
" |
|
|
|
|
|
|
|
2о |
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
||
Разделить |
окруж- |
|
|
|
|
1О" |
|
|
|
|
|
4о |
3о |
|
|
1 |
|
|
|
|
|||||
нат. вел. |
|
|
|
5о |
|
|
|
ие |
|
|
|
Линия |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ность сечения на 6 |
образующих |
|
|
|
|
|
|
н |
|
|
|
||||||||||||||
6о |
|
|
|
|
2 |
ече |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|||
частей и перенести |
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
с |
|
|
|
|
|
||||
|
|
|
|
|
|
|
н |
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
ь |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
ол |
ое |
|
5 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
зв |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||||
точки |
1-6 |
парал- |
|
и |
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
||||||
о |
|
|
|
ь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
р |
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
п |
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
м |
|
е |
|
ь) |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
ор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
н |
|
|
|
|
и |
|
|
ст |
хорда |
|
|
|
|
|
|
|
|
|
||||
лельно |
оси конуса |
|
|
|
|
ен |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
ч |
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
е |
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
S |
||||||||
|
с |
|
|
уж |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
кр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
на линию |
сечения |
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(проекцию |
окруж- |
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
S" |
|
б |
|
|
|
|
|
ности), то есть по- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9.7 |
|
|
|
|
|
|
||
строить точки 1о-6о. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3-е действие. Через вершину конуса S(S") и точки 1о-6о провести об- |
|||||||||||||||||||||||||
разующие конуса до пересечения с проекцией линии пересечения с проек- |
|||||||||||||||||||||||||
цией линии пересечения цилиндра и конуса О1"-6". |
|
|
|
|
|
|
|||||||||||||||||||
4-е действие. Вращением построенных образующих вокруг оси кону- |
|||||||||||||||||||||||||
са перенести точки 1о"-5о" на очерковую образующую S"-6", имеющую на |
|||||||||||||||||||||||||
чертеже натуральную величину. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
5-е действие. На свободном поле чертежа провести радиусом R=S"Оо |
|||||||||||||||||||||||||
дугу и отложить на этой дуге шесть отрезков-хорд, на которые было поде- |
|||||||||||||||||||||||||
лено сечение конуса. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6-е действие. Через точку S на развертке и построенные точки Оо-6 |
|||||||||||||||||||||||||
провести семейство образующих. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
7-е действие. Отложить от точек Оо-6 на каждой образующей развертки |
|||||||||||||||||||||||||
соответствующие натуральные величины образующих, взятые с чертежа, |
|||||||||||||||||||||||||
то есть отрезки 6о-1о, 6о-2о и т. д. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
8-е действие. Построенные на концах семейства образующих точки |
|||||||||||||||||||||||||
соединить плавной кривой и оформить чертеж развертки (построена поло- |
|||||||||||||||||||||||||
вина развертки). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
152

На рис. 9.8 показано построение развертки боковой поверхности боковой поверхности усеченного конуса (если вершину конуса на чертеже достроить нельзя) с основаниями, равными d и D.
Предварительно на чертеже усеченного конуса строится вспомогательный неусеченный конус подобный заданному так, чтобы отношение диаметра D исходного конуса к диаметру вспомогательного конуса d, было целым число, то есть K = D/d1 – целое число, где K – коэффициент кратности оснований конусов.
Примем K = 3 и впишем в заданный конус вспомогательный конус с вершиной S".
Достроим горизонтальную проекцию вспомогательного конуса и разделим половину окружности основания d1 на 6 частей (1-6).
Далее приступаем к построению развертки половины усеченного конуса по следующему графическому алгоритму:
1-е действие. На свободном поле чертежа построить развертку вспомогательного конуса с вершиной S (см. рис. 9.8), то есть построить точки 0-2-4-6 на дуге развертки.
2-е действие. На оси симметрии развертки (биссектриса полной развертки) выбрать произвольную точку К и провести семейство лучей, соединяющих соответственно произвольную точку К с точками 0-2-4-6 развертки вспомогательного конуса.
3-е действие. Отложить на проведенных лучах отрезки, величины которых определяются произведениями:
конус, подобный заданному
d
L
|
d1 |
|
|
|
D |
2 |
3 |
4 |
|
||
1 |
|
5 |
|
S' |
6 |
0' |
n6 |
|
|
|
|
6о |
|
6 |
|
K6о=K·K6 |
|
|
|
n4 |
|
|
L |
|
|
4о |
|
|
2о |
Рис. 9.8
L |
S |
|
произвольная  K точка
K точка
4 |
|
|
n2 |
2 |
nо |
|
||
|
|
|
|
|
Линия симметрии |
|
|
0о |
КОо = К×КО;
К2о = К×К2; К4о = К×К4; К6о = К×К6,
где К – принятый коэффициент пропорциональности, а величины КО, К2, К4 и К6 следует измерить на строящейся развертке.
На концах лучей определяются
точки Оо, 2о, 4о и 6о.
4-е действие. Через построенные точки на концах лучей провести прямые n0-n6, каждая из которых должна быть соответственно параллельна образующим вспомогательного конуса на его развертке.
5-е действие. На проведенных прямых n0-n6 отложить натуральную величину длин образующих заданного усеченного конуса L.
153
6-е действие. Оформить чертеж развертки, соединив построенные точ- |
||||||||||
ки развертки лекальными прямыми. |
|
|
|
|
|
|||||
У с л о в н ы е р а з в е р т к и п о в е р х н о с т е й |
|
|
||||||||
Условные развертки можно выполнить для некоторых неразвертыва- |
||||||||||
ющихся поверхностей. |
|
|
|
|
|
|
|
|
||
Рассмотрим построение условных разверток неразвертывающихся по- |
||||||||||
верхностей сферы и открытого тора (кругового кольца). |
|
|
||||||||
Развертка сферической поверхности |
|
|
||||||||
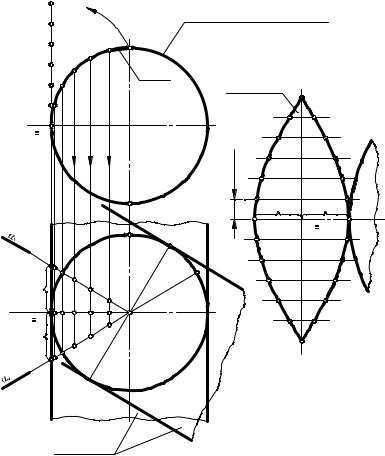
На рис. 9.9 показано построение условной развертки сферической по- |
||||||||||
верхности. |
|
|
|
|
|
|
|
|
|
|
Поверхность сферы |
хордам |
А |
|
|
|
|
|
|
||
условно разрезают на ка- |
1 |
|
|
|
Очерк сферы совпадает с |
|
||||
кое-то количество частей |
по |
|
|
|
очерком описанного цилиндра |
|
||||
|
|
1" |
АО" |
|
||||||
дуги |
2 |
|
|
|
|
|||||
(6, 12 и более) и каждую |
2" |
|
|
|
||||||
|
|
|
|
|
|
|||||
3 |
3" |
|
|
|
|
|
||||
часть заменяют (аппрок- |
Развертка |
|
хорда |
|
|
|
||||
4 |
4" |
|
1/6 доля |
А |
|
|||||
симируют) |
цилиндриче- |
|
|
|
|
|||||
5 |
5" |
|
|
развертки |
|
|||||
|
|
|
|
|||||||
ской описанной поверх- |
6" |
|
|
0 |
|
1 |
|
|||
|
|
|
|
|
||||||
ностью, фронтальная про- |
Со 6" |
|
|
|
|
2 |
|
|||
|
|
|
|
|
хорда |
|
||||
екция которой совпадает |
|
|
|
|
|
3 |
|
|||
с фронтальным очерком |
|
|
|
|
|
4 |
|
|||
|
|
|
|
|
|
|
||||
сферы – окружностью. |
|
|
|
|
Во |
6о |
5 |
6о |
||
Далее |
|
выполнятся |
|
|
|
|
|
|
Со 6 |
|
развертка одной доли по- |
|
|
|
|
|
|
|
|
||
верхности сферы как сек- |
|
6о' |
2о |
|
|
|
|
|
||
тора цилиндрической по- |
|
|
|
1о |
|
|
|
|||
1/6 сферы |
|
|
|
|
|
|||||
верхности по следующе- |
Со 6' |
5' 4' 3' 2' 1' |
А' |
|
|
|
||||
му графическому алго- |
|
|
2о |
1о |
|
|
|
|
||
ритму: |
|
|
|
6о' |
|
|
|
В |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
1-е действие. На го- |
|
|
|
|
|
|
|
|
||
ризонтальной |
проекции |
|
|
|
|
|
|
|
|
|
разрезать |
поверхность |
|
|
|
|
|
|
|
|
|
сферы на 6 частей и рас- |
|
|
Описанные |
|
|
|
|
|||
смотреть эту |
1/6 часть |
|
|
цилиндры |
|
|
|
|
|
|
(сектор) как фронтально- |
|
|
|
|
|
Рис. 9.9 |
|
|
||
проецирующий цилиндр, |
|
|
|
|
|
|
|
|
||
описанный вокруг сферы. |
|
|
|
|
|
|
|
|
||
2-е действие. Разделить дугу очерковой окружности А0В0 сферы, ко- |
||||||||||
торая совпадает с окружностью описанного цилиндра, на 12 частей (по- |
||||||||||
скольку есть симметрия, рассматриваем дугу А0С0) и заменить участки |
||||||||||
хордами (то есть вписать 12-угольную призму) – А0"-1", 1"-2" и т. д. |
|
|||||||||
3-е действие. Спроецировать точки 1"-6" на стороны взятого сектора |
||||||||||
его горизонтальной проекции. |
|
|
|
|
|
|
|
|||
154

4-е действие. Свободном поле чертежа провести вертикальную линию |
|||||||||||||
и отложить от точки С0 вверх и вниз по 6 отрезков, равных величине хорд |
|||||||||||||
(точки пронумеровать). |
|
|
|
|
|
|
|
|
|
||||
5-е действие. Через каждую построенную точку А-6 провести гори- |
|||||||||||||
зонтальные линии и на каждой отложить величину соответствующей обра- |
|||||||||||||
зующей: 10-10, 20-20 и т. д. |
|
|
|
|
|
|
|
|
|
||||
6-е действие. Конечные точки соединить лекальной кривой. |
|
|
|||||||||||
Таким образом построена 1/6 доля условной поверхности сферы, а 6 та- |
|||||||||||||
ких долей составят развертку всей поверхности. |
|
|
|||||||||||
С увеличением количества долей (1/12, 1/24 и т. д.) точность разверт- |
|||||||||||||
ки увеличивается. |
|
|
|
|
|
|
|
|
|
|
|||
Развертка поверхности открытого тора |
|
|
|||||||||||
На рис. 9.10 показана условная развертка поверхности открытого тора. |
|||||||||||||
Поверхность кольца разрезают на какое-то количество долей (6, 12 |
|||||||||||||
и более) плоскостями, проходящими через его ось i", и заменяют каждую |
|||||||||||||
долю (сектор) поверхно- |
|
|
описанный |
|
|
|
|
||||||
|
|
|
цилиндр |
|
|
|
|
|
|||||
сти описанной цилиндри- |
|
|
|
|
|
|
|
|
|
||||
ческой поверхностью. |
|
|
|
|
|
|
|
|
|
||||
Далее выполняют раз- |
|
|
|
|
|
|
1/6 развертки |
6 |
6о |
||||
вертку одной доли поверх- |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||
|
1о |
|
|
|
|
поверхности тора |
5 |
|
|||||
ности |
по |
|
графическому |
0о |
2о |
|
|
|
|
5о |
|||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||
алгоритму, |
приведенному |
|
|
|
3о |
|
|
|
4 |
4о |
|||
|
|
|
|
4о |
|
|
|||||||
для построения развертки |
1/6 тора |
|
|
|
5о 6о |
3 |
3о |
||||||
одной |
доли |
поверхности |
|
|
|
|
|
|
|
||||
|
|
|
|
|
i" |
2 |
|
||||||
сферы. |
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
2о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На рис. 9.11 приведен |
|
|
|
|
|
|
|
1 |
1о |
||||
|
|
|
|
|
|
|
|
||||||
чертеж построения части |
|
|
|
|
|
|
0 |
0 |
0 |
||||
(правой) развертки комби- |
0о |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
нированной |
геометриче- |
|
|
|
|
|
|
|
|
|
|||
ской поверхности, состоя- |
|
|
|
|
|
|
|
|
|
||||
щей из трех полых цили- |
|
|
|
|
|
|
|
|
|
||||
ндров, |
сообщенных двумя |
|
|
|
|
|
|
|
|
|
|||
коническими рукавами, в |
0' |
|
|
|
|
|
6' |
|
|
||||
котором подытоживается |
1' |
|
|
|
|
|
5' |
|
|
||||
изученный материал дан- |
|
|
|
|
|
|
|
||||||
хорда |
|
2' |
|
4' |
|
|
|
||||||
ной темы. |
Показано, что |
|
|
3' |
|
|
|
|
|
||||
|
|
|
Очерк образующей тора |
|
|
||||||||
|
|
|
|
|
|
||||||||
развертка |
каждой |
части |
|
|
|
|
совпадает с поверхностью |
|
|
||||
|
|
|
|
цилиндра |
|
|
|||||||
комбинированной поверх- |
|
|
|
|
|
|
Рис. 9.10 |
|
|
||||
ности строится отдельно. |
|
|
|
|
|
|
|
|
|
||||
Структуризация материала девятой лекции в рассмотренном объеме |
|||||||||||||
схематически представлена на рис. 9.12 (лист 1). На последующих листах |
|||||||||||||
2–5 компактно приведены иллюстрации к этой схеме для визуального за- |
|||||||||||||
крепления изученного материала при повторении (рис. 9.13–9.16). |
|
||||||||||||
155

156 |
|
|
|
|
|
|
|
|
|
|
|
дополнительная |
|
хорда |
|
|
|
|
|
симметрииинияЛ |
|
||
|
|
|
|
|
70 |
|
|
|
|
|
|
образующая |
|
|
|
дополнительная |
|
|
|
||||
6 5 |
|
4 |
|
|
3 |
2 |
1 О |
|
|
|
6 |
5 |
4 |
|
F 3 |
2 |
|
|
1хорда |
О |
|||
|
|
|
|
|
K3 |
K4 |
1 О1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О1 |
D |
|
|
|
|
3 |
2 |
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
K1 |
K2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
G |
|
|
|
|
K5 |
K6 |
E |
О4 |
|
|
|
|
|
|
F0 |
|
20 |
|
10 |
|
|
О1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
F0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
|
|
4 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
40 |
|
|
|
|
|
|
|
|
|
|
|
хорда |
|
|
|
|
|
|
||||
|
|
20 |
50 |
|
|
хорда |
|
|
|
хорда |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 |
|
|
|
40 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
K7 |
K8 |
дополнит-я |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О4 |
|
|||||
|
|
|
|
|
6 |
F |
3 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
2 |
1 |
|
||||||
|
|
|
|
|
|
5 |
4 |
|
|
02 |
|
|
50 |
|
|
3 |
|
|
|
||||
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
L |
|
|
5 |
4 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ч т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е ь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
я |
|
|
|
|
|
|
|
6 5 4 |
3 |
2 1 03 |
|
|
|
|
|
50 |
40 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F0 |
20 |
|
0 |
02 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
хорда |
|
|
|
F 3 |
|
|
|
|
|
|
Sк |
|
|
|
|
|
|
|
|
|
|
О2 |
|
дополнит-я |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
D2=70-d2 |
|
4 |
|
|
|
|
хорда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5 |
|
|
|
|
|
1 |
4 |
3 |
2 |
хорда |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О3 |
|||||||
|
|
|
|
|
|
|
|
5 |
|
1 |
|
|
|
|
|
6 |
5 |
4 |
3 2 |
1 |
|||
6 |
|
|
|
|
L |
|
6 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
О О1 |
|
О2 |
О3 |
Sк |
|
|
|
|
|
|
хорда |
|
|
SK |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
БНТУ |
Графическая работа № |
|
D1=70-d1 |
Разраб. |
Вар. |
|
Провер. |
Гр. |
||
|
Рис. 9.11

Развертки поверхностей |
Ðèñ. 9.13, à |
Ðèñ. 9.16, á |
Ðèñ. 9.13, á |
Ðèñ. 9.15, à |
Ðèñ. 9.15, á |
Ðèñ. 9.14 |
Ðèñ. 9.16, à |
Ëèñò 1 |
Рис. 9.12 |
157 |

Развертки поверхностей
10.1. Развертка гранных поверхностей
Развертка призмы.
а. Способ нормального сечения (применяется, если на чертеже ребра призмы являются прямыми уровня)
|
|
|
В" |
2" |
V - нормальное сечение |
|
|
|
|
|
|
Х1 |
|
|
|
|
|
|
|
|
|
A" |
С" |
|
|
|
V Н1 |
|
3" |
|
D" |
|
||
|
|
|
|
21' |
||
|
|
|
|
|
|
|
н.в. ребер |
|
1" |
|
|
D1' |
|
|
|
|
|
|
у |
|
V |
А' |
|
1' |
|
11' |
31' |
|
|
|
||||
Х Н |
|
|
|
|
|
|
|
|
у |
В' |
2' |
|
натуральная вели- |
|
|
|
D' |
чина сечения |
||
|
|
С' |
|
3' |
|
|
ребро A
1
Линии |
A |
сгиба |
|
ВС
2


 3
3 

 1
1
 D
D
à.
Рис. 10.1
Графический алгоритм:
1.Построить натуральную величину нормального сечения, перпендикулярного к ребрам призмы.
2.Развернуть стороны сечения в линию и из вершин, провести направления ребер перпендикулярно к линии развертки.
3.Отложить вверх и вниз от точек вершин натуральные отрезки ребер и соединить построенные вершины; провести линии сгиба на месте ребер тонкими штрихпунктирными линиями с двумя штрихами.
б. Способ раскатки (применяется, если на чертеже ребра являются прямыми уровня и есть натуральная величина основания)



 N
N
N"
К" (M")
(M")
А" К' А'
 М'
М' 
(N')
Геодезическая
линия
К М
М
R=С'А' |
|
|
АО |
ВО |
|
R=А'В' |
||
|
 СО
СО
R=В'С'
С" В"


 В'
В'
 С'
С'
Графический алгоритм построения на чертеже геодезической линии:
1.Построить развертку поверхности призмы.
2.Построить на развертке заданные на
поверхности точки (M и N) и соединить прямой геодезической линией, которая пересекает ребро A в т.K.
3. Вернуть построенную т.K на проекции призмы и соединить с заданными точками M и N ломаной линией с учетом ее видимости на поверхности.
á.
Ëèñò 2
Рис. 9.13
158

Развертки поверхностей
Развертка поверхности пирамиды.
|
|
S" |
i" |
|
Н.в. ребер |
|
|
|
|
|
|
|
|
|
|
|
|
|
Н.в. SA |
|
|
|
|
|
|
|
|
К" |
|
|
1О |
КО" |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
МО" |
|
|
|
В" |
А" |
С" |
|
|
О |
mО |
О |
" |
m" |
|
|
С " |
В |
||||
А' |
|
|
|
|
|
|
|
|
|
М' |
S' |
i' |
|
СО' |
mО |
ВО' |
|
m' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В' |
К' |
N' 1' |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
С'
|
|
|
|
à. |
|
Н.в. SA |
Линии сгиба |
|
|
А |
|
|
S |
Графический алгоритм построения развертки |
|
|
|
|
поверхности пирамиды: |
М |
|
|
|
1. Построить натуральные величины всех |
|
|
|
ребер пирамиды (способом вращения вокруг |
|
m |
|
|
|
|
К |
|
|
проецирующей оси). |
|
|
|
|
||
|
|
|
2. Выполнить развертку поверхности, |
|
В |
|
N 1 |
|
|
|
|
построив по натуральным величинам ребер |
||
|
|
|
|
треугольники граней и основание. |
|
|
|
|
3. Соединить отрезками построенные на |
Геодезическая |
С |
|
|
развертке вершины и оформить линии сгиба. |
линия |
|
|
|
|
|
|
|
|
|
|
|
осн. |
А |
|
á. В
В
Ëèñò 3
Рис. 9.14
159
