свойства ферромагнетиков (у них, например, большая магнитная восприимчивость, имеет место явление гистерезиса), но проявляются слабее. Многие ферримагнетики являются полупроводниками и обладают малой электропроводностью. Такие ферримагнетики называются ферритами. Являясь достаточно сильными магнетиками, они имеют малые тепловые потери при работе на высоких частотах.

Как и у ферромагнетиков, у антиферромагнетиков и ферримагнетиков при нагреве выше определенной температуры (у антиферромагнетиков она называется температурой Нееля) нарушается упорядоченность структуры расположения магнитных моментов атомов и они превращаются в парамагнетики.

3.6. Сверхпроводники в магнитном поле

Как ранее отмечалось [5], при некоторой критической температуре Tк происходит переход многих проводников в сверхпроводящее состояние.

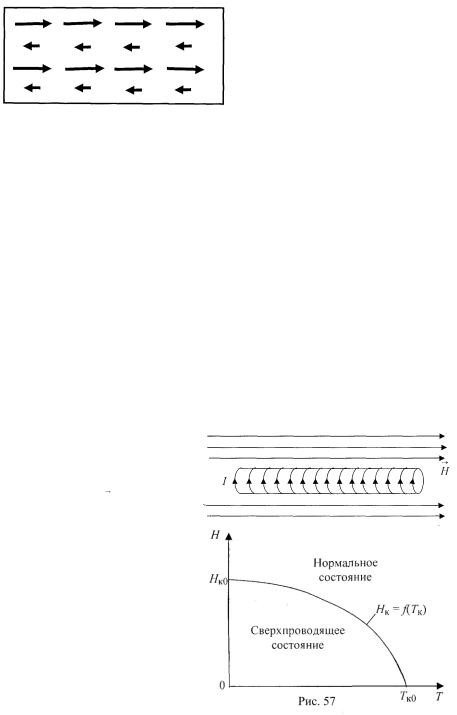
температура тем ниже, чем больше напряженность этого поля. На рис. 57 показана зависимость величины критической напряженности

58

нормального в сверхпроводящее состояние, от критической температуры Tк. Как видно из рисунка, при H > Hк и T > Tк образец находится в

нормальном состоянии, а при H < Hк и T < Tк − в сверхпроводящем. Представленная зависимость хорошо описывается формулой

При переходе образца, находящегося во внешнем магнитном поле, в сверхпроводящее состояние, либо при помещении во внешнее магнитное поле образца, уже находящегося в этом состоянии, происходит вытеснение магнитного поля из образца. Вытеснение магнитного поля из образца, находящегося в сверхпроводящем состоянии, называется эффектом Мейснера. Причина этого явления состоит в том, что на поверхности образца возникают токи, магнитное поле которых компенсирует внешнее магнитное поле внутри образца. Эти токи текут в тонком поверхностном слое сверхпроводника. Толщина этого слоя составляет 10−8–10−7 м. На такую же глубину проникает в сверхпроводник и магнитное поле. На рис. 56 показаны такие токи, текущие по поверхности цилиндрического образца. Применяя выражение (3.27), получаем, что в сверхпроводнике

т. е. J = − H. Следовательно, магнитная восприимчивость сверхпроводника χ = J/H = −1, а его магнитная проницаемость μ = 0. С формальной точки зрения сверхпроводник можно рассматривать как идеальный диамагнетик.

Существуют сверхпроводники первого рода и сверхпроводники второго рода. У сверхпроводников первого рода переход цилиндрического образца, находящегося в продольном магнитном поле (рис. 56), в сверхпроводящее состояние происходит сразу во всем объеме. Именно

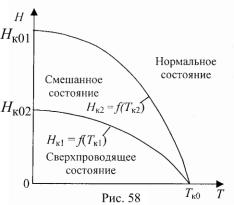
состояние (рис. 58). В этом состоянии объем образца состоит из сверхпроводящих областей и

59

областей, имеющих обычную проводимость. Из областей с обычной проводимостью магнитное поле не вытесняется. Пусть цилиндрический образец, являющийся сверхпроводником второго рода, помещен в продольное внешнее магнитное поле (рис. 56). В этом случае области нормальной проводимости представляют собой трубки, вдоль которых проходят линии магнитного поля, параллельные линиям внешнего магнитного поля. Толщина трубок имеет порядок 10−7 м. Внутри трубок циркулируют круговые токи, охватывающие сердцевину трубки.

Объяснение свойств сверхпроводников может быть дано в рамках квантовой физики.

60