
Волны
.pdf
удовлетворяет волновому уравнению (1.15).
Пусть в однородной и изотропной упругой среде распространяется продольная бегущая волна. Выделим в упругой среде физически малый элемент объема в виде прямого цилиндра, левое основание которого в состоянии равновесия (при отсутствии волны) имеет координату z , а правое основание – координату z dz (рис. 5). Если вдоль оси z распространяется волна, то рассматриваемый элемент объема совершает колебания около положения равновесия, сопровождающиеся деформациями элемента. В нижней части рис. 5 показано положение этого элемента в некоторый момент времени. Левое основание цилиндра смещено от положения равновесия на величину , а правое основание
– на величину d (рис. 5). |
|
Величина d представляет собой |
|
абсолютную |
деформацию |
цилиндра, |
вызванную |
прохождением продольной волны. |
|
Отношение |
деформации |
элемента объема d к длине dz |
|
недеформированного |
элемента |
(частицы) |
называется |
относительной деформацией : |
|
||
|
d |
. |
(1.18) |
|
|||
|
dz |
|
|
При деформации растяжения (рис. 5) |
0 . При деформации сжатия |
||
0 . Чтобы получить выражение для относительной деформации, следует взять производную от уравнения волны (1.17) по z :
|
|
|
z |
|
|
|
z |
m sin t |
|
|
, (1.19) |
|
|||||
|
|
|
|
||
где m a – амплитуда относительной деформации.
Вторая производная по координате z определяется формулой
Рис. 5
2 |
|
a 2 |
|
z |
|
|||
|
|
|
|
|
cos t |
|
. |
(1.20) |
z |
2 |
|
2 |
|
||||
|
|
|
|
|
|
|||
Первая производная по времени характеризует колебательную скорость рассматриваемого элемента объема, которую не следует путать со скоростью распространения волны
|
|
z |
|
|
|
t |
m sin t |
|
|
, |
(1.21) |
|
|||||
|
|
|
|
||
где m a – амплитуда колебательной скорости.
11
Вторая производная по времени характеризует ускорение частицы упругой среды:
2 |
|
2 |
|
z |
|
||
t |
2 |
a |
|
cos t |
|
. |
(1.22) |
|
|
||||||
|
|
|
|
|
|
||
Сравнивая правые части (1.20) и (1.22), получим волновое уравнение для плоской продольной волны, распространяющейся в направлении оси
Z,
2 1 2 .z2 2 t2
(1.23)
Полученный результат означает, что уравнение бегущей волны (1.7) удовлетворяет волновому уравнению.
Можно показать, что волновому уравнению (1.23) удовлетворяют
любые |
функции |
от аргументов t z и t z |
, т. |
е. функции вида |
|||
(t z |
) |
и (t z |
) . Такие функции описывают распространение в среде |
||||
со скоростью |
возмущений произвольной формы |
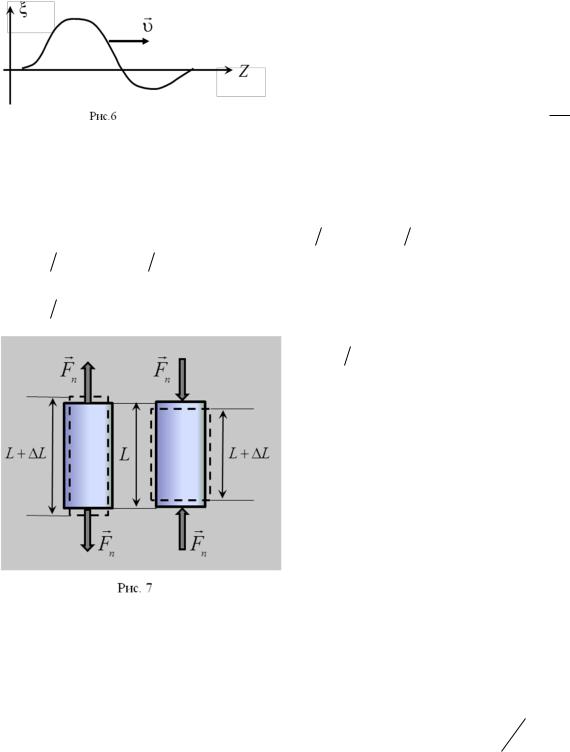
(рис. 6). Функция |
|||||
(t z |
) |
|
соответствует возмущению, движущемуся |
в положительном |
|||
|
|
|
|
|
направлении оси Z (рис. 6), а функция |
||
|
|
|
|
|
(t z ) |
– |
возмущению, |
|
|
|
|
|
движущемуся |
в |
противоположном |
|
|
|
|
|
направлении. |
|
|
|
|
|
Рис. 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.4. Скорость распространения продольной волны в твердом теле
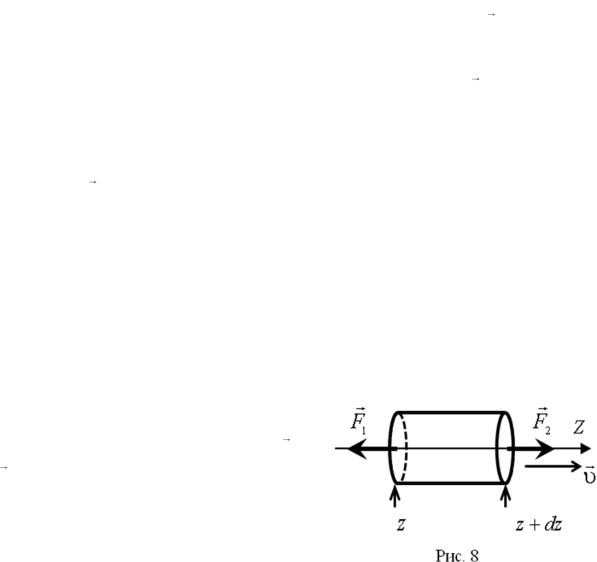
Распространение продольной волны в твердом теле связано с упругими деформациями сжатия и растяжения. На рис. 7 изображены
деформации растяжения (слева) и сжатия (справа) цилиндра длиной L, площадью сечения S под действием сил Fn, направленных вдоль оси цилиндра перпендикулярно его основанию.
Как показывает опыт, при небольших упругих деформациях относительная деформация с хорошей степенью точности оказывается
пропорциональной величине нормального напряжения σ Fn |
S |
: |
||
|
|
|
|
|
|
1 |
, |
|
(1.24) |
Е |
|
|||
|
|
|
|
|
12
где – коэффициент пропорциональности, зависящий от материала твердого тела. Коэффициент называется коэффициентом упругости, а
обратная ему величина E* – модулем Юнга. Равенство (1.24), выражающее закон Гука, может быть записано в виде
E* . |
(1.25) |
Для силы нормального напряжения получим |
|
F S E S . |
(1.26) |
n |
|
Найдем связь скорости распространения продольной волны со свойствами среды, в которой она распространяется.
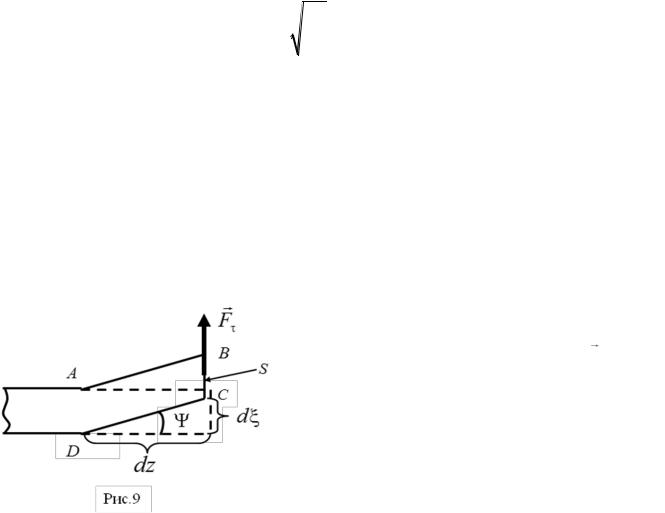
Пусть в однородном твердом теле распространяется продольная плоская упругая волна в направлении оси Z со скоростью . Выделим в этом теле физически малый объем (рис. 8) в форме прямого цилиндра с осью, совпадающей с осью Z. Введем обозначения: dm – масса цилиндра; dz
– длина рассматриваемого цилиндра. Тогда силу |
F1 , |
создающую |
нормальное напряжение в точках сечения с координатой |
z , согласно |
|
формуле (1.26) можно определить так: |
|
|
F E S (z) . |
|
(1.27) |
1 |
|
|
Сила F2 , создающая нормальное напряжение в |
точках сечения с |
|
координатой z dz , в соответствии с (1.26) определяется формулой |
||
F E S (z dz) . |
|
(1.28) |
2 |
|
|
Относительная деформация среды в точках сечения с координатой z dz отличается от относительной деформации среды в точках сечения с координатой z и может быть представлена в виде разложения в ряд Тейлора. Ограничившись первыми двумя членами разложения, получим
|
|
(z dz) (z) |
|
dz ... |
(1.29) |
||||
|
|
z |
|||||||
|
|
|
|
|
|
|
|
|
|
Деформация |
физически |
малого |
|
|
|
|
|
||
объема, изображенного на рис. 8, |
|
|
|
|
|
||||
соответствует растяжению: силы F1 |
и |
|
|
|
|
|
|||
F2 направлены в противоположные |
|
|
|
|
|
||||
стороны. При деформации сжатия эти |
|
|
|
|
|
||||
силы |
также |
направлены |
в |
|
|
|
|
|
|
противоположные |
стороны, |
но |
|
|
|
|
|
||
|
|
|
Рис. 8 |
|
|||||
навстречу |
друг |
другу. |
Поэтому, |
|
|
|
|
||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
применяя второй закон Ньютона к рассматриваемому физически малому объему и учитывая соотношения (1.27)–(1.29), для результирующей силы, равной F2 F1 , получим
13
dm |
2 |
F |
F |
E S |
(z) dz (z) |
|
E S dz E S |
2 dz . (1.30) |
|||
|
t |
2 |
2 |
1 |
|
|
z |
|
z |
z |
2 |
|
|
|
|
|
|
|
|
||||
При переходе к последнему равенству в (1.30) учтено, что |
d |
. |
|
||
|
dz |
|
Найдем массу dm рассматриваемого объема dV : |
|
|
dm dV S dz , |
(1.31) |
|
где – плотность материала твердого тела.
После подстановки (1.31) в (1.30) и сокращений приходим к
соотношению |
|
|
|
|
|
|
2 |
E 2 . |
(1.32) |
||||
t2 |
|
|
z2 |
|
||
Сравнивая (1.32) с волновым уравнением |
|
|||||
2 |
|
1 2 |
(1.33) |
|||
|
2 |
|
|
|
2 , |
|
z |
2 |
t |
||||
|
|
|
|
|
||
можно сделать вывод, что распространение продольной волны в однородном изотропном твердом теле происходит со скоростью
|
|
E |
|
. |
(1.34) |
|
|
||||||
|
|
|
|
|
Как видно из (1.34), скорость распространения плоской продольной бегущей волны зависит от упругих свойств и плотности материала, из которого состоит тело.
1.5.Скорость распространения поперечной волны
втвердом теле
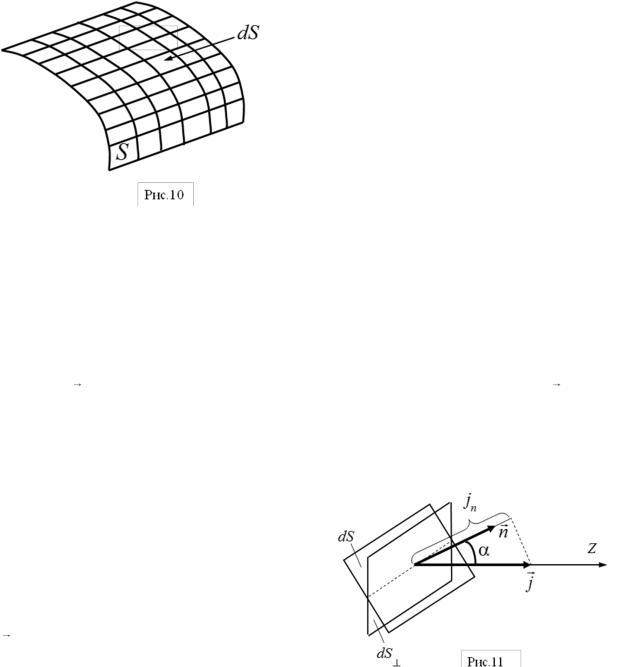
Распространение поперечной волны в твердом теле связано с упругими деформациями сдвига. На рис. 9 представлена деформация сдвига, при которой все слои твердого тела, параллельные плоскости сдвига AD, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу. Сдвиг
происходит под действием силы Fτ ,
приложенной касательно к грани BC, параллельной плоскости сдвига. Мерой деформации в этом случае является угол сдвига , который при малых упругих деформациях пропорционален
14

касательному напряжению |
Fτ |
: |
|
|
|
|
|
|
|
|
|
|
|
||
|
S |
|
|
|
|
|
|
|
|
|
1 |
|
Fτ |
, |
(1.35) |
|
|
|
|
||||
|
|
|
G S |
|
|||
где величина G называется модулем сдвига и является характеристикой упругих свойств материала, из которого состоит твердое тело. Как видно из рис. 9, при малых деформациях
tg |
d |
. |
(1.36) |
|
|||
|
dz |
|
|
Подставляя в (1.35) вместо величину , получаем выражение для |
|||
силы |
|
||
F G S . |
(1.37) |
||
Равенство (1.36) имеет вид, аналогичный выражению (1.26).
Проводя рассуждения, аналогичные сделанным для продольной волны (1.27)–(1.33) в п. 1.4, приходим к следующей формуле для скорости поперечной волны:
|
G |
. |
(1.38) |
|
|||
|
|
|
|
1.6. Энергия, плотность энергии упругой волны
Рассмотрим однородную упругую среду, в которой распространяется продольная плоская бегущая волна в направлении оси Z со скоростью . Выделим в этой среде физически малый объем в форме прямого цилиндра с осью, параллельной оси Z (рис. 8). Используем ранее введенные
обозначения: dz – |
длина, S |
– |
|
площадь |
поперечного |
сечения |
||||||
рассматриваемого |
цилиндра, |
– |
|
плотность |
упругой среды. |
Масса |
||||||
рассматриваемого объема dV цилиндра определяется формулой |
|
|
||||||||||
|
|
dm S dz dV . |
|
|
|
(1.39) |
||||||
Пусть величина |
|
представляет собой |
усредненное |
по |
всему |
|||||||
|
t |
|
|
|
|
|
|
|
|
|
|
|
физически малому объему |
dV |
значение колебательной скорости частиц. |
||||||||||
Определим кинетическую энергию dWк |
в объеме dV : |
|
|
|||||||||
|
|
1 |
|
2 |
|
1 |
|
2 |
|
|
||
|
dWк |
|
dm |
|
|
|
|
dV |
|
. |
|
(1.40) |
|
|
|
|
|
||||||||
|
|
2 |
|
t |
|
|
2 |
|
t |
|
|
|
Объемная плотность кинетической энергии
15

|
dW |
1 |
|
2 |
|
|
wк |
к |
|
|
|
. |
(1.41) |
|
|
|||||
|
dV |
2 |
|
t |
|
|
Рассматриваемый объем обладает также потенциальной энергией упругой деформации dWп , для рассмотрения которой вспомним свободные
колебания пружины под действием упругой силы kx , где k –
жесткость пружины [3]. Потенциальная энергия колебаний, связанная с упругими деформациями пружины, определяется по формуле
|
|
|
W |
1 |
|
kx2 |
|
1 |
|
Fx |
|
. |
|
|
|
|
|
|
|
|
(1.42) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
п |
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Учитывая, что в случае упругого объема выражение для силы имеет |
|||||||||||||||||||||||||||||
вид (1.26) и что роль деформации пружины |
x |
|
в данном случае играет |
||||||||||||||||||||||||||
деформация объема d (рис. 5), получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1 |
* |
|
|
|
1 |
|
|
|
* |
|
|
d |
|
|
|
|
|
1 |
|
* |
2 |
dV . |
(1.43) |
|||||
dWп |
|
E |
S d |
|
|
|
E |
|
|
|
|
|
|
S dz |
|
|
E |
|
|
||||||||||
2 |
2 |
|
|
|
dz |
2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Используя ранее полученное соотношение (1.34), определим |
|||||||||||||||||||||||||||||
объемную плотность потенциальной энергии: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
w |
dWп |
|
|
1 |
E* 2 |
1 |
|
2 2 . |
|
(1.44) |
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
п |
|
dV |
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Выражение для объемной плотности полной энергии волнового поля получим суммированием плотности кинетической (1.41) и плотности потенциальной (1.44) энергий:
|
|
|
w |
1 |
|
2 |
1 |
|
2 |
. |
(1.45) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
t |
|
2 |
|
|
|
|
Используя выражения (1.19) и (1.21), можно показать, что оба |
||||||||||||
слагаемых в (1.45) равны друг другу: |
|
|
|
|
|
|
||||||
w |
1 |
2a2 sin2 ( t kz) |
1 |
2a2 sin2 |
( t kz) 2a2 sin2 ( t kz) . (1.46) |
|||||||
|
|
|||||||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
Таким образом, объемные плотности кинетической и потенциальной энергии в волновом поле бегущей волны одинаковы и зависят одинаково от времени и координаты.
Найдем среднее по времени значение объемной плотности энергии. В случае гармонической волны (1.17) в качестве промежутка времени, по которому проводится усреднение, удобно взять период колебаний. Так как среднее за период значение квадрата синуса равно 0,5, то из (1.46) получаем для среднего за период значения плотности энергии
|
|
|
1 |
2a2 . |
(1.47) |
|
w |
||||||
|
2 |
|||||
|
|
|
|
|
16
Как видно из (1.46) и (1.47), максимальное и среднее значения плотности энергии волны пропорциональны плотности упругой среды , квадрату частоты и квадрату амплитуды колебаний.
1.7. Поток, плотность потока энергии. Интенсивность волны
Для описания процесса переноса волной энергии вводятся величины:
поток энергии, плотность потока энергии, интенсивность волны.
Потоком энергии через произвольную поверхность S называется величина
|
|
|
|
dW |
, |
|
(1.48) |
|
|
|
|
|
|||
|
|
|
|
dt |
|
|
|
|
|
где dW – энергия, перенесенная волной |
|||||
|
|
через эту поверхность за время dt . Если |
|||||
|
|
за одинаковые промежутки времени t |
|||||
|
|
волна переносит через поверхность S |
|||||
|
|
одинаковую энергию W , то можно |
|||||
|
|
сказать, что поток энергии – это энергия, |
|||||
|
|
переносимая |
волной |
через |
эту |
||
|
Рис. 10 |
||||||
|
поверхность за единицу времени. |
|
|||||
|
|
|
|||||
Через одинаковые по площади участки поверхности S |
волна может |
||||||
переносить разное количество энергии за один и тот же промежуток времени. Для описания этого различия вводится понятие плотности потока энергии. Разделим поверхность S на элементарные площадки dS (рис. 10), настолько малые, чтобы в пределах выбранной площадки характеристики волны и среды можно было считать одинаковыми. Рассмотрим перенос энергии через одну из таких площадок dS (рис. 11). Проведем ось Z в направлении переноса энергии волной в точках этой площадки. Проведем нормаль n к площадке. Пусть – угол между осью Z и нормалью n (рис.
11). Проекция |
площадки |
dS |
на плоскость, |
перпендикулярную оси Z , |
||||
определяется формулой |
|
|
|
|
|
|||
|
|
|
|
dS dS cos . |
(1.49) |
|||
Площадка |
dS |
перпендикулярна |
|
|
|
|||
направлению переноса энергии волной. |
|
|
|
|||||
Очевидно, что поток энергии через |
|
|
|
|||||
площадки dS и dS |
одинаков. |
|
|
|
||||
Плотностью |
потока |
|
энергии |
|
|
|
||
(вектором Умова) называется вектор |
|
|
|
|||||
j , направление которого совпадает с |
|
|
|
|||||
|
|
|
||||||
направлением |
переноса |
энергии |
|
|
|
|||
Рис. 11 |
||||||||
волной, а |
модуль |
определяется |
||||||
равенством |
|
|
|
|
|
|
|
|
17
j |
|
d |
|
, |
(1.50) |
|
dS |
||||||
|
|
|
|
|||
где d – поток энергии, перенесенной волной |
через площадку dS , |
|||||
перпендикулярную направлению переноса энергии. Из определения потока энергии (1.48) следует, что модуль плотности потока энергии можно записать следующим образом:
j |
|
dW |
|
|
, |
(1.51) |
|
|
|
|
|||
dt dS |
|
|||||
|
|
|
|
|
||
где dW – энергия, перенесенная волной за время dt через площадку dS . Из равенств (1.50) и (1.49) следует
d j dS j dS cos . |
(1.52) |
Учтем, что |
|
j cos jn |
(1.53) |
является проекцией плотности потока энергии на направление нормали n к площадке dS (рис. 11). Тогда поток через площадку dS можно записать в виде
|
d |
jn dS . |
|
|
(1.54) |
|
Полный поток через поверхность |
S может быть найден как сумма |
|||||
потоков через все элементарные площадки |
dS , |
на которые разделена эта |
||||
поверхность (рис. 10): |
|
|
|
|
|
|
d jdS |
jndS . |
|
(1.55) |
|||
S |
S |
|
S |
|
|
|
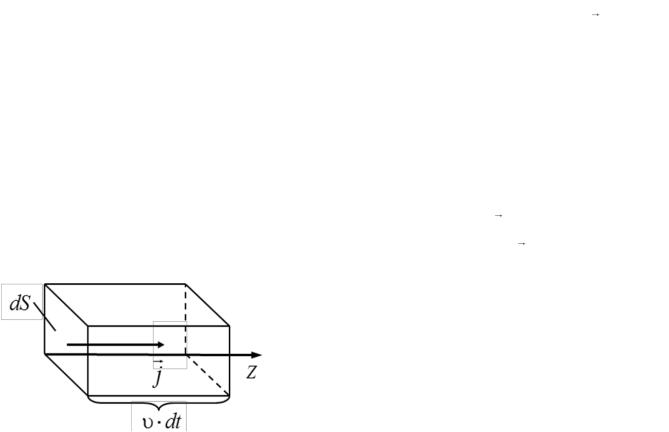
Найдем связь между плотностью потока |
энергии j |
и |
объемной |
|||
плотностью w этой энергии в бегущей волне. Пусть вектор |
j |
направлен |
||||
|
вдоль оси Z (рис. 12). Через площадку |
|||||
|
dS , перпендикулярную этой оси, за |
|||||
|
время dt волна перенесет энергию |
|||||
|
|
|
|
dW j dS dt . |
(1.56) |
|
|
За это же время dt фронт волны |
|||||
|
переместится |
на расстояние |
dt , и |
|||
|
волна заполнит энергией объем |
|||||
Рис. 12 |
|
|
|
dV dS dt . |
(1.57) |
|
Определим энергию, заключенную в этом объеме: |
|
|
||||
dW w dV w dS dt . |
|
(1.58) |
||||
Приравнивая (1.56) и (1.58) и сокращая на dS dt , получаем |
|
|||||
18

j w . |
(1.59) |
Учитывая, что вектор плотности потока энергии j и вектор скорости волны в бегущей волне направлены одинаково, можем записать:
j w . |
|
|
|
(1.60) |
|||||
В частности, для плоской бегущей гармонической волны, используя |
|||||||||
выражение (1.46), получаем |
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
2 |
|
z |
|
||
j a |
|
|
sin |
|
t |
|
. |
(1.61) |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
Интенсивностью волны I называется среднее по времени (за период |
|||||||||
колебаний) значение плотности потока энергии. Из (1.61) получаем |
|
||||||||
I |
1 |
2a2 . |
|
|
(1.62) |
||||
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
||
Рассмотрим сферическую волну в однородной среде и покажем, что у нее зависимость амплитуды колебаний от расстояния r до источника имеет вид, соответствующий выражению (1.14). Потерями энергии в среде на нагревание и излучение будем пренебрегать. Источник волны считаем расположенным в начале координат: r 0 .
Рассмотрим две концентрические сферы, в центре которых находится источник волны: одна радиуса r0 , другая радиуса r . Пусть r r0 .
Очевидно, средний за период поток энергии, проходящий через эти две сферы, должен быть одинаков ввиду отсутствия потерь энергии:
(r) (r0 ) . |
(1.63) |
Интенсивность волны и ее амплитуда во всех точках каждой из этих сфер должны быть одинаковыми ввиду одинаковой удаленности точек от источника. Используя выражение (1.55) для потока, учитывая, что в данном случае плотность потока направлена по нормали к поверхностям сфер и,
следовательно, jn j , получаем из (1.63) |
|
|
|
I (r) 4 r2 I (r ) 4 r 2 |
, |
(1.64) |
|
0 |
0 |
|
|
где I (r) и I (r0 ) – интенсивность на расстояниях соответственно r и r0 от источника. Отсюда
|
r2 |
|
|
I (r) |
0 |
I (r ) , |
(1.65) |
|
|||
|
r2 |
0 |
|
|
|
|
т. е. плотность потока энергии и интенсивность в сферической волне убывают обратно пропорционально квадрату расстояния от источника волны. Формула (1.62), связывающая интенсивность с амплитудой волны, была получена для плоской волны. Однако все выкладки, с помощью которых она была получена, остаются справедливыми и для сферической
19
волны с заменой координаты z на r . Подставляя теперь (1.62) в равенство (1.65), для амплитуды волны получим
a(r) |
r0 |
a(r ) , |
(1.66) |
|
|||
|
r |
0 |
|
|
|
|
где a(r) и a(r0 ) – амплитуды колебаний в сферической волне на расстояниях соответственно r и r0 от источника. Обозначая r0 a(r0 ) a0 ,
получаем амплитуду, как в формуле (1.14). Таким образом, амплитуда колебаний в сферической волне убывает обратно пропорционально расстоянию от источника волны.
1.8. Стоячие волны
Стоячая волна образуется при наложении двух распространяющихся навстречу друг другу плоских волн с одинаковым направлением колебаний с равными частотами и амплитудами. Так происходит, например, при сложении падающей и отраженной от преграды бегущей волны.
Рассмотрим основные особенности стоячей волны.
Пусть вдоль оси Z распространяются навстречу друг другу две волны, уравнения которых имеют вид
1(z,t) a cos( t kz); |
(1.67) |
2 (z,t) a cos( t kz) . |
(1.68) |
Результирующее колебание является суммой этих колебаний:
(z,t) 1(z,t) 2 (z,t) a[cos( t kz) cos( t kz)]. |
(1.69) |
Применяя известную тригонометрическую формулу, приходим к выражению
|
2 |
|
|
|
|
(z,t) 2a cos kz cos t 2a cos |
|
z |
cos t . |
(1.70) |
|
|
|||||
|
|
|
|
При переходе к последнему выражению учтена формула (1.6), дающая связь волнового числа k и длины волны . Полученное выражение называется уравнением стоячей волны.
Величину
|
|
2 |
|
|
|
|
|
||||
A(z) |
2a cos |
|
z |
(1.71) |
|
|
|||||
|
|
|
|
называют амплитудой стоячей волны. Из выражения (1.70) следует, что колебания в стоячей волне происходят с частотой , равной частоте складываемых волн. Амплитуда волны (1.71) зависит от координаты z. В точках среды, где
2 z |
m , |
m 0,1, 2,..., |
(1.72) |
|
|
||||
|
|
|
20
