
Новый НИРС / NIRS_Novikov_SM9-91
.pdf3 Создание цифрового двойника робота в Matlab Simulink
Цифровой двойник робота в Matlab Simulink будет представлять собой комплексную модель, включающую несколько подсистем, которые описывают различные аспекты работы робота: математическую модель аккумуляторной батареи, кинематику робота и систему управления на основе заданных эксплуатационных циклов. Ниже приведено детальное описание каждой из этих подсистем.
3.1 Математическая модель аккумуляторной батареи (модель
Шеферда)
Наиболее простой моделью ТАБ, описывающей процессы в аккумуляторе при изменении зарядно-разрядного тока, является модель Шеферда. На рисунке 11 изображена теоретическая форма разрядной кривой,
предсказываемая данной моделью. Данное уравнение в режиме разряда аккумулятора выглядит следующим образом (1):
где
= |
− |
|
|
− |
|
+ (− ) − , |
(1) |
|
+ 0,1 |
− |
|||||||
0 |
|
|
|
0 |
|
0 – максимальное напряжение аккумулятора, В;
0 – внутреннее сопротивление, Ом;
K – поляризационная составляющая, В;
А – экспоненциальная составляющая, В;
В – инверсная экспоненциальная составляющая, Ач−1; Q – полная емкость аккумулятора, Ач;
– интегральный ток, А.
|
|
= ∫ |
|
, |
(2) |
|
|
|
|
|
|
|
|
- ток разряда аккумулятора, А. |
|
||
|
|
|
|
|
|
21
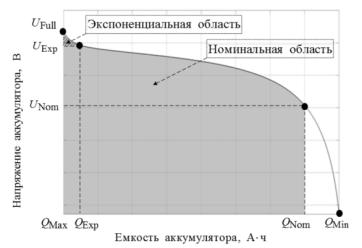
Рисунок 11 – Форма зависимости напряжения ТАБ от емкости в модели Шеферда
В данной работе воспользуемся моделью Шеферда для оценки разрядной характеристики имеющейся батареи, и уточним её характеристики.
Значения параметров для данной модели найдем по следующим выражениям
(3-7):
|
|
|
|
= |
− ; |
|
|
|
|
(3) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
3 |
|
; |
|
|
|
|
(4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
− |
|
+ (− − 1)) |
( |
− ) |
(5) |
||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
1 − |
|
; |
|
|
(6) |
|||||
|
|
|
0,2 |
|
|
|
|
||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
= |
|
+ − + ; |
|
(7) |
|||||||||
|
|
|
|
|
|||||||||||
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|||
где – максимально допустимое напряжение аккумулятора, В;
– экспоненциальное напряжение аккумулятора, В;
– номинальное напряжение аккумулятора, В;
– номинальная емкость аккумулятора, Ач;
22

– максимальная емкость аккумулятора, Ач;
– экспоненциальная емкость аккумулятора, В;
– КПД аккумулятора, %.
Таким образом, опираясь на модель литий-полимерного аккумулятора Шеферда были рассчитаны основные параметры, требующиеся для подтверждения теоретической модели по имеющимся экспериментальным данным, и представлены в таблице 2.
Таблица 2 – Параметры математической модели ТАБ.
Параметр |
Значение |
|
|
, В |
0,3 |
|
|
, Ач−1 |
15 |
|
|
, В |
0,036 |
|
|
0, Ом |
0,39 |
|
|
0, В |
3,43 |
|
|
, А |
0,2 |
|
|
, мА/ч |
0,13 |
|
|
3.2 Кинематика робота
Кинематическая модель робота описывает движение робота в пространстве на основе управляющих сигналов, поступающих от системы управления. Робот имеет два ведущих колеса, каждое из которых управляется отдельным двигателем.
Найдем линейную скорость робота по формуле (8):
= + , 2
где и — скорости левого и правого электромоторов.
Угловая скорость робота вычисляется по формуле (3):
= | − |,
где — расстояние между колёсами.
23
(8)
(9)
Положение робота определим по формулам (4): |
|
̇= ( ) |
|
̇= ( ) |
(10) |
|
|
̇= , |
|
где ( , ) — координаты робота, — угол поворота. |
|
3.3 Система управления роботом
Система управления роботом генерирует управляющие сигналы для двигателей на основе заданных эксплуатационных циклов вождения. Цикл вождения — это последовательность точек данных, представляющих зависимость скорости транспортного средства от времени, и включают в себя движение по прямой с различной скоростью, частые ускорение и торможение. Циклы вождения разрабатываются различными странами и организациями для оценки характеристик транспортных средств по разным параметрам, например, по расходу топлива, автономности электромобилей и выбросам загрязняющих веществ. Разрабатываемый робот предназначен для исследования тяговых аккумуляторных батарей, аналогичных используемым в электромобилях, и, как следствие, имеет смысл исследовать характеристики ТАБ в условиях эксплуатации как у электромобилей.
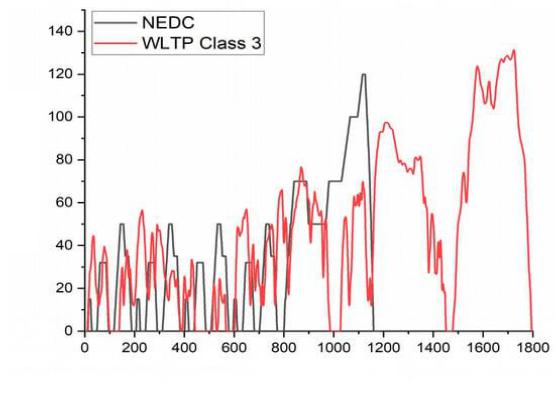
Наиболее популярным на данный момент является цикл WLTP, который был принят Комитетом по внутреннему транспорту Европейской экономической комиссии ООН (ЕЭК ООН) в качестве дополнения № 15 к Глобальному реестру (Глобальным техническим правилам), определенному Соглашением 1998 года. Стандарт принят Китаем, Японией, США и Европейским союзом, а также другими странами. Он призван заменить предыдущий региональный Новый европейский цикл вождения (NEDC) в качестве новой европейской процедуры сертификации транспортных средств. Новый стандарт был разработан таким образом, чтобы лучше соответствовать
24
реальным и современным условиям вождения. Для достижения этой цели
WLTP длится на 10 минут дольше, чем NEDC а его профиль скорости более динамичен и состоит из более быстрых ускорений с последующим коротким торможением. Кроме того, средняя и максимальная скорости были увеличены до 46,5 км/ч и 131,3 км/ч соответственно. Пройденное расстояние составляет
23,25 км (более чем в два раза больше 11 километров NEDC). Цикл WLTP
разделён на 4 части, каждая из которых имеет свою максимальную скорость:
Низкий - до 56,5 км/ч; Средний - до 76,6 км/ч; Высокоскоростной - до 97,4
км/ч; Сверхвысокоскоростной - до 131,3 км/ч.
Эти этапы вождения имитируют городские, пригородные, сельские и автомагистральные сценарии соответственно, с равным распределением городских и загородных маршрутов (52% и 48%).
На рисунке 12 изображены циклы вождения NEDC и WLTP class 3.

 Скорость, км/ч
Скорость, км/ч
Время, с
Рисунок 12 – Различие между ездовыми циклами NEDC и WELP class 3
В Matlab Simulink ездовые циклы движения задаются с помощью блока
Drive Cycle Source, который генерирует стандартный или заданный
пользователем ездовой цикл. Однако, в состав пакета Matlab входит только
25
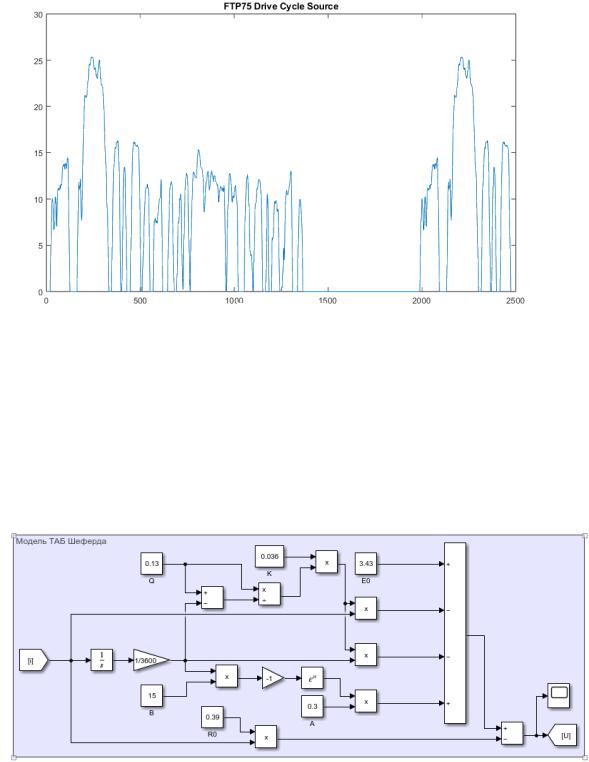
цикл FTP75, изображенный на рисунке 13, как наиболее популярный на территории США, что не является проблемой, так как оба этих цикла близки по смыслу.
Скорость, м/с
Время, с
Рисунок 13 – Цикл вождения FTP75, реализованный в блоке Drive Cycle Source в Matlab Simulink
3.4 Реализация модели в Matlab
На рисунках 14-19 приведена реализация цифровой модели робота в
Matlab Simulink.
Рисунок 14 – Модель ячейки тяговой аккумуляторной батареи Шеферда
26
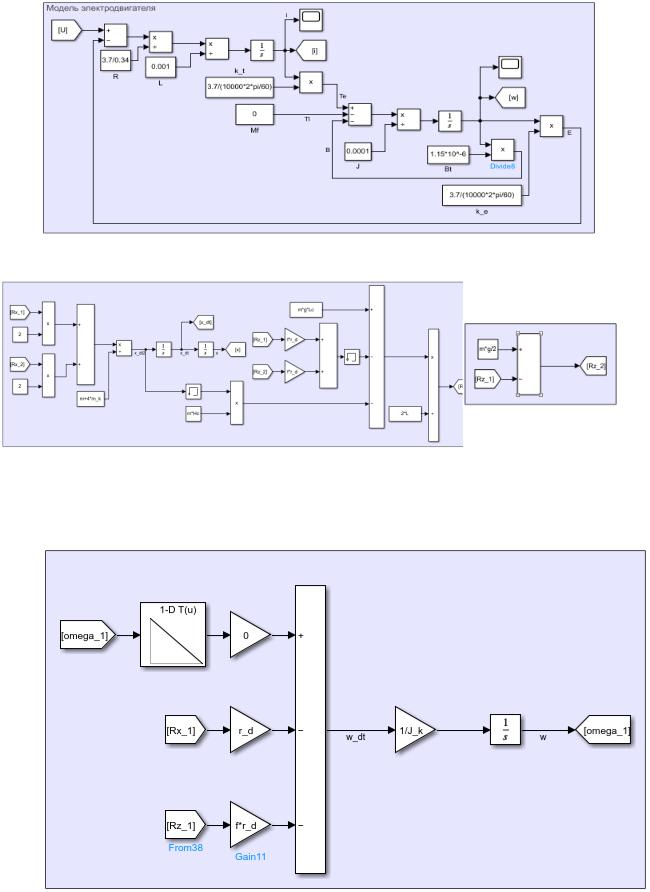
Рисунок 15 – Модель электродвигателя, питаемого бортовой батареей
Рисунок 16 – Модель динамики корпуса робота
Рисунок 17 – Модель вычисления скорости ведомых колес
27
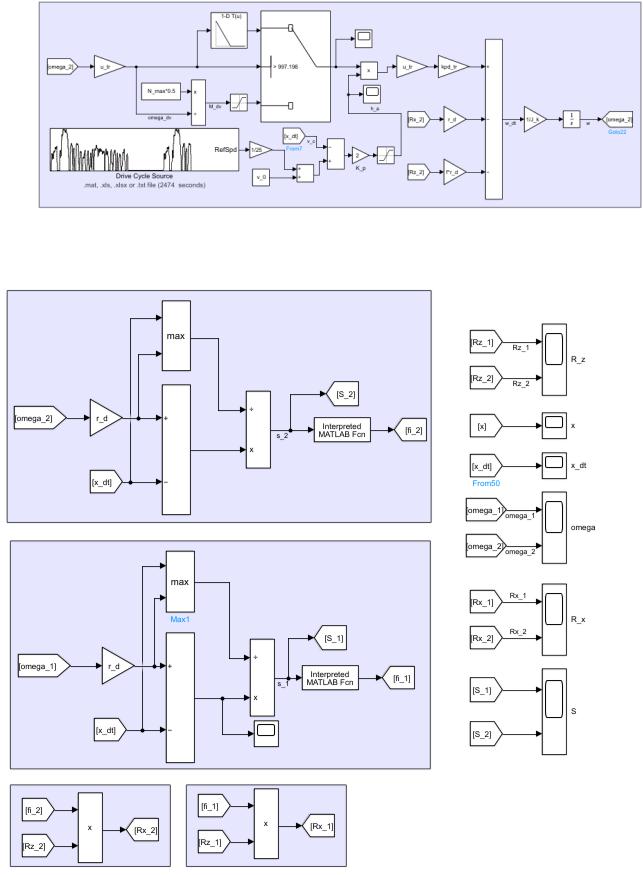
Рисунок 18 – Модель вычисления скорости ведущих колес в соответствии с заданной скоростью по циклу движения
Рисунок 19 – Модель вычисления коэффициентов скольжения,
горизонтальных реакций и вывод графиков движения.
28
4 Исследование энергопотребления робота на основе цифрового
двойника
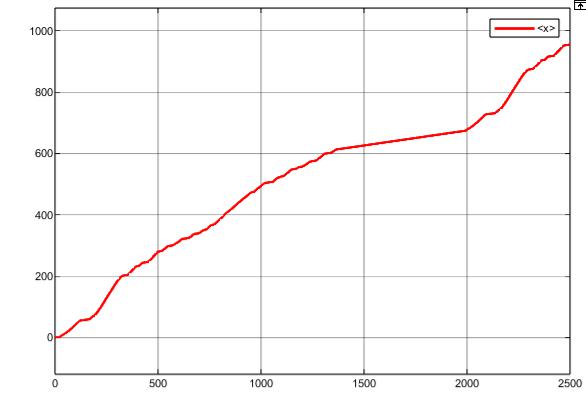
На рисунке 20 изображена зависимость перемещения робота от времени при движении по циклу FTP75. На данном графике отчетливо видна изначальная структура цикла, содержащая как периоды резкого ускорения и движения на большой скорости, так и периоды движения на минимальной скорости, близкой к нулю.
Перемещение робота, м
Время, с Рисунок 20 – Зависимость перемещения робота от времени при движении по
циклу FTP75.
На рисунках 21-22 изображена зависимость линейной скорости робота и угловых скоростей колес робота от времени. Данные рисунки полностью повторяют собой внешний вид заданного цикла движения, но отличаются по высоте – максимальной скорости движения, в силу малого размера робота.
29
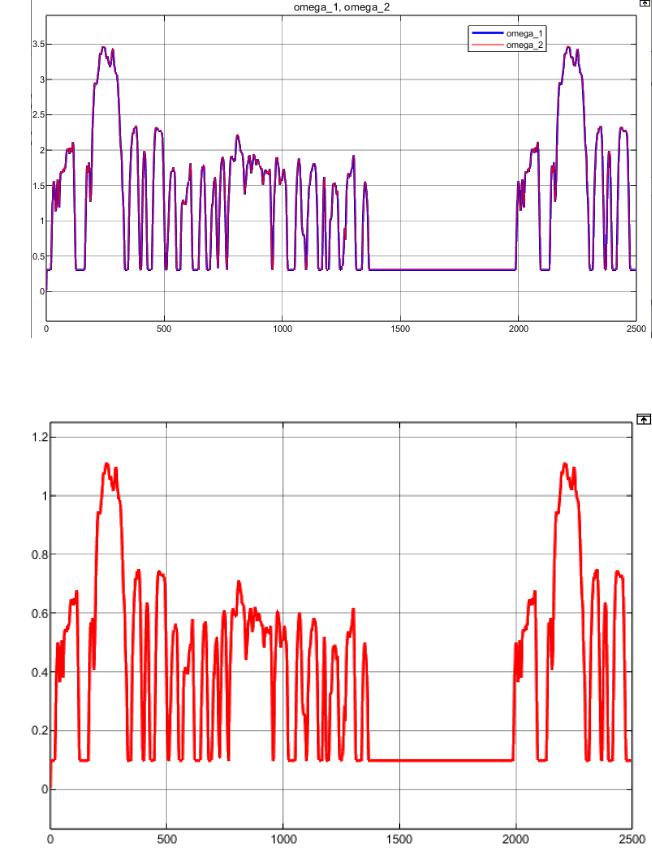
Угловая скорость колес, рад/с
Время, с Рисунок 21 – Зависимость угловой скорости колес (осей) робота от времени
при движении по циклу FTP75
Линейная скорость робота, м/с
Время, с Рисунок 22 – Зависимость линейной скорости робота от времени при
движении по циклу FTP75
30
